Одной из задач, решаемых при создании робототехнических систем, является задача компенсации взаимовлияния звеньев исполнительного механизма через статическую и динамическую нагрузку. Цель компенсации – улучшение качества управления роботом. При этом, как правило, вычисляют составляющие (гравитационную, центробежную, кариолисову и инерционную) общей нагрузки, действующей в движущемся исполнительном механизме манипулятора, и формируют соответствующие корректирующие воздействия в структуре системы управления [1, 2, 7]. Частным случаем компенсации гравитационных нагрузок является статическая разгрузка с помощью механических устройств, пневмо- или гидроцилиндров [2, 7], которые, при этом, решают задачу улучшения энергетических и массогабаритных показателей.
При динамическом анализе манипулирующих систем исполнительный механизм традиционно рассматривается как совокупность звеньев (жестких или упругих), соединенных кинематическими парами. Такое рассмотрение исполнительного механизма предопределяет одноканальное представление позиционных взаимосвязей и силовых взаимодействий через систему «звенья – кинематические пары» при любом методе описания динамических свойств манипулятора. В то же время, например, вращательная кинематическая пара пятого класса вращающийся момент, действующий вокруг оси пары, не передает. Влияние одного звена на другое, соединенных такой парой, в процессе движения происходит через силы и реактивные моменты механизма передачи движения и других конструктивных элементов. Это обстоятельство указывает на возможность компенсации (уменьшения) взаимовлияния звеньев на этапе структурного синтеза исполнительного механизма.
Для анализа этих возможностей наиболее удобно воспользоваться обобщенным уравнением Даламбера, которое в явном виде отражает влияние эффектов движения звеньев на динамику им роботов. Согласно [6] уравнение движения вращательного звена им можно записать в виде
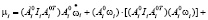
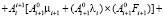
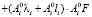. (1)
Здесь µi – момент в i-м шарнире ИМ;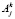 
(при j, k = 0,1,2, …i … n) матрицы преобразования однородных координат в виде представления Денавита-Хартанберга; (х0, у0, z0 – базовая система координат); Ii – тензор инерции; 
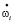– условное ускорение звена; ?i – его угловая скорость; ?i – положение i-ой системы координат относительно начала (i-1)-й системы координат; Fi+1 – сила, действующая со стороны i + 1 звена на i-е звено; li – положение центра масс i-го звена в i-й системе координат; Fi – суммарная сила, приложенная к центру масс i-го звена.
Из рассмотрения выражения (1) момент влияния других звеньев на i-звено сводится к выражению
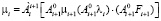. (2)
Как было отмечено ранее, вращательная пара 5-го класса момент не передает (относительно оси вращения), то в соответствии с выражением (2) существует потенциальная возможность исключить (или уменьшить) влияние момента µi+1 на µi .
Представим момент µi+1 в виде пары сил fi+1 на некотором сколько угодно малом, не приводящем к образованию статического нуля, плече ri+1, расположенном в плоскости движения звеньев. В случае приложения к концам плеча ri+1 двух параллельных удерживающих связей сила fi+1 раскладывается по правилу параллелограмма на составляющие усилия fi+1 =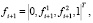 
где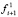 
– взаимно противоположные составляющие, действующие вдоль связей, 
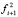– взаимно противоположные составляющие, действующие вдоль плеча ri+1. Выражение для момента µi+1 с учетом выполненного разложения будет иметь вид:
.
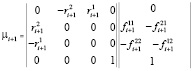Здесь цифрами указано разложение на оси координатной системы, выбор которых произволен.
Поскольку усилия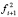 
равны, взаимно противоположны и действуют по одной прямой, то в случае приложения удерживающих связей в плоскости i-го звена, получим
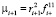. (4)
Из (4) следует, что в случае приложения в шарнирах i-го звена удерживающих связей, таких, чтобы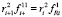 
, где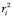 
– плечо действия реакций связей 
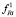в i-м шарнире момент µi+1 будет оказывать малое (лишь через диссипативные силы, действующие в шарнирах) влияние на величину момента µi. Изложенное выше справедливо как для статических моментов, так и динамических, обусловленных относительным движением.
Для трансформирования статических моментов в шарниры с целью разложения на пары сил необходим синусно-косинусный механизм преобразования активного момента в реактивный. На рис. 1 изображен механизм [4] который в наибольшей степени подходит для решения поставленной задачи.
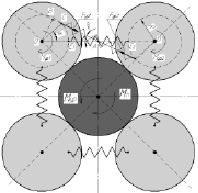
Рис. 1. Синусно-косинусный механизм разгрузки
Он представляет собой несколько зубчатых колес одинакового диаметра. Центральное колесо жестко соединено со звеном манипулятора, а четыре другие колеса закреплены в корпусе. Центральное колесо вращается под действием статического момента нагрузки, а остальные обкатываются вокруг него; пружины растягиваются и создают при этом cилы, стремящееся вернуть их в начальное положение, тем самым создавая уравновешивающий момент. Уравновешивающий момент зависит от количества колес, обкатываемых вокруг центрального, соотношения диаметров колес, количества пружин, установленных на каждом колесе, жесткости пружин и мест их крепления к колесам. Особенностью данного синусно-косинусного механизма является то, что он позволяет получить замкнутый силовой поток.
Момент нагрузки Мн, возникающий от силы тяжести звена, определяется выражением
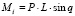, (5)
где Р – сила тяжести звена, L – плечо действия силы, q – угол отклонения звена от начального положения. Уравновешивающий момент равен отношению момента нагрузки к КПД синусно-косинусного механизма:
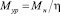. (6)
Рассмотрим условия создания уравновешивающего момента одной пружиной при равенстве диаметров всех колес (рис. 2). Точки крепления пружины Е1 и Е2 находятся на одинаковом расстоянии от осей поворота колес.
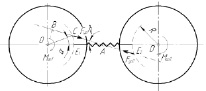
Рис. 2. Создание уравновешивающего момента одной пружиной
Уравновешивающий момент Мур1, создаваемый одной пружиной, равен:
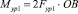; (7)
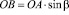. (8)
По теореме синусов имеем
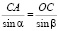. (9)
Из (9) получаем
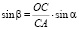. (10)
Подставляем (10) в (8) и получаем
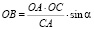(11)
Тогда, подставляя (11) в (7), получим
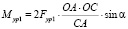. (12)
Имеем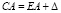 
, где ? – деформация пружины при растяжении.
Полагая, что
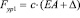, (13)
получим
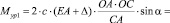
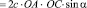. (14)
Для всех N пружин
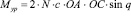. (15)
Так как sin q = sin ?, то
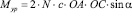. (16)
Подставляя (16) в (7) и (6), имеем
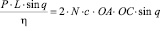. (17)
Из (17) выразим жесткость одной пружины с:
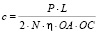. (18)
После расчета параметров пружин следует проверить работоспособность системы статической моментной разгрузки на компьютерной модели.
В механизмах сложной структуры, например, с параллельной кинематикой уравновешивающий момент может иметь сложную зависимость. В этом случае, для компенсации неуравновешенности можно использовать переменное передаточное отношение зубчатых колес (рис. 3).
Необходимый уравновешивающий момент можно представить в следующем виде:
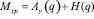, (19)
где Ay(q) – уравновешивающий момент, обеспечиваемый исходным синусным механизмом; H(q) – остаточный момент неуравновешенности. Величина H(q) может быть получена в результате численного моделирования, в общем случае, как нелинейная функция от q. Эту нелинейную функцию можно представить некоторой аналитической зависимостью, например, кубическим сплайном после интерполяции или экстраполяции исходной графической зависимости. Кубический сплайн будет иметь вид
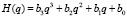. (20)
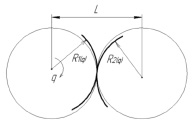
Рис. 3. Колеса с переменным передаточным отношением
На основании выражений (19) и (20) полное уравновешивание механизма может обеспечить момент, определяемый выражением (21):
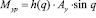, (21)
где h(q) – некоторая нелинейная функция, величину которой можно определить из соотношения
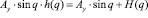. (22)
После преобразования получим
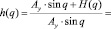
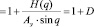. (23)
Из рассмотрения рис. 3 имеем
; 
;
.
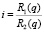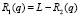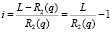Тогда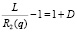 
; 
;
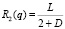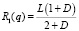. (24)
Выражения (24) определяют переменные радиусы зубчатого зацепления при обеспечении полной уравновешенности механизма.
Библиографическая ссылка
Умнов В.П. КОМПЕНСАЦИЯ ВЗАИМОВЛИЯНИЯ И СТАТИЧЕСКАЯ РАЗГРУЗКА В МАНИПУЛЯЦИОННЫХ ИСПОЛНИТЕЛЬНЫХ СИСТЕМАХ РОБОТОВ // Современные наукоемкие технологии. – 2015. – № 12-3. – С. 448-451;URL: https://top-technologies.ru/ru/article/view?id=35290 (дата обращения: 16.04.2024).