Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Дасибеков А. 1 Юнусов А.А. 2 Айменов Ж.Т. 1 Юнусова А.А. 3 Саржанова М.Ж 1

---

1 Южно-Казахстанский государственный университет имени М. Ауэзова

2 Международный гуманитарно-технический университет

3 Казахская Академия труда и социальных отношений

Данная работа посвящена решению одномерной задачи уплотнения грунтов, обладающих упругоползучим свойством. Здесь часть нагрузки, равная величине структурной прочности сжатия, сразу же воспринимается скелетом грунта. Кроме того, уплотняемый грунт по своей структуре неоднороден. Причем свойство неоднородности грунтового основания учитывается через его модуль деформации, который изменяется по глубине в виде экспоненциальной функции. Для изучения процесса уплотнения грунтового массива в такой постановке под действием различных внешних сил получен ряд расчетных формул. При помощи этих выражений можно определить давление в поровой жидкости, напряжение в скелете неоднородного уплотняемого грунта и вертикальные перемещения точек верхней поверхности земляного массива для любого момента времени.

Статья в формате PDF

2947 KB

процесс

уплотнение

грунт

прямоугольник

давления

основания

фундамент

граничные условия

1. Абелев М.Ю. Строительство промышленных и гражданских сооружений на слабых водонасыщенных грунтах. – М.: 1983. – С. 59–66.

2. Абжапбаров А.А. К решению нелинейной двумерной задачи механически упруго-ползучих неоднородных грунтов // Актуальные вопросы развития образования и науки: мат. межд.науч.-теорет.конф., посв. 10-летию образования ЮК ПУ. – Шымкент, 2003. – Т. 2. – С. 371–376.

3. Попов Г.Я. К теории изгиба плит на упругом неоднородном полупространстве // Строительство и архитектура. – 1959. – № 12. – С. 11–19.

4. Флорин В.А. Основы механики грунтов. – М.: Госстройиздат, Т.2. 1961. – С. 60–276.

5. Ширинкулов Т.Ш., Дасибеков А.Д., Бердыбаева М.Ж. О трехмерном уплотнении упругоползучих неоднородных грунтов с неоднородными их граничными условиями // Механика и моделирование технологических процессов. – Тараз, 2006. – № 1. – С. 30–35.

К разработке данной темы подтолкнули разрушения отдельных высотных сооружений, построенных в регионах Южного Казахстана. Безусловно, такие разрушения зданий явились последствием неправильного расчета грунтовых оснований и в основном связаны с тем, что здесь не учитывались вопросы консолидации, ползучести и их неоднородность.

Результаты многочисленных исследований фундаментов и грунтовых оснований жилых сооружений позволяют предположить наличие крупных зон деформации верхней части земной коры, в которых породы обладают пониженной прочностью и по которым могут активно циркулировать подземные воды. Над такими зонами обычно происходят аномальные осадки зданий, результатом которых являются их деформации и повреждения. Этого можно избежать, если при проектировании своевременно учесть некоторые факторы, сильно влияющие на уплотнение массива. Одним из таких факторов является неоднородность грунтов по составу, генезису, физико-механическим свойствам в основании фундаментов инженерных объектов, обусловленная сложным геолого-тектоническим строением верхней части земной коры того или иного региона Казахстана. Верхняя часть земной коры многих регионов Казахстана характеризуется высокой степенью неоднородности слагающих ее грунтов, пород, и невнимание к таким неоднородностям земляных масс во время проектирования оснований может привести в будущем к повреждениям инженерных сооружений вследствие их неравномерной осадки. В качестве такого примера можно привести некоторые жилые здания, которые не дошли до эксплуатации (рисунок).

В связи с этим в данной работе приведены разработанные реологическая математическая модель и аналитический метод исследования линейного деформирования неоднородного упругоползучего грунтового основания. Здесь математическая модель неоднородного грунтового основания состоит: из типовой схемы, представляющей самого основания; из уравнения состояния элементов структуры грунтового основания σ_i = f(ε_i) из системы краевых условий, которые определяются в соответствии с классификацией поставленной задачи как краевой задачи математической физики; из условия равновесия системы; из искомого решения. Причем неоднородность грунтового массива учитывается через модуль его деформации, который в математическом виде может быть представлен в виде экспоненциальной функции глубины, использованной Г.Я. Поповым в [3] при исследовании контактных задач теории упругости, т.е.

E = E₀e^αz (0 < α < 1), (1)

где E₀, α – опытные данные. Выражение (1) также использовано в работах [2, 5].

Упругоползучее состояние неоднородного грунта описывается зависимостью вида:

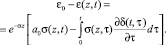(2)

Здесь мера ползучести неоднородного грунта выражена следующей зависимостью:

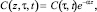(3)

где a₀ – коэффициент сжимаемости однородного грунта; e₀ и e – коэффициенты пористости для начального и конечного моментов времени; σ – напряжение в скелете грунта; C(τ, t) – мера ползучести однородного грунта. Она определяется по формуле 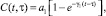[4]:

(4)

где a1, γ1 – параметры ползучести; t – момент приложения внешней нагрузки; E(z) – модуль общей деформации, зависящий от координаты z; a1, γ – параметры ползучести; δ(z, t, τ) – относительная деформация от единичной силы.

Из (4) при величине C(τ, t) = 0 находим выражение, совпадающее с компрессионной зависимостью, которая отражает упругое состояние неоднородного грунта. При значениях α = 0, C(τ, t) ≠ 0 имеем случай уплотнения упругоползучего однородного грунта. Однако при дальнейшем исследовании считаем, что α ≠ 0, и этот параметр принимает значения, лежащие только в интервале (0, 1).

Далее пусть грунт считается неоднородной упругоползучей двухфазной средой, и она подвержена действию внешней нагрузки q(z, t). Ёе верхняя поверхность уплотняемой грунтовой среды находится под песчаной подушкой, т.е. поверхность водопроницаема, а её нижняя поверхность водонепроницаема. Тогда граничные условия данной задачи при ламинарном законе Дарси примут вид:

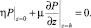(5)

Жилые здания, которые не дошли до эксплуатации

В (5) при z = 0 величина, μ = 0, а при z = h значение η = 0. Здесь, когда величина μ = 0, первое граничное условие задачи относится к уплотнению слоя грунта с устройством песчаной подушки на нем, а при значении μ = 0, второе граничное условие относится к глубине h, ниже которой фильтрации не происходит. Величина порового давления P(z, t) при t = τ1 будет равна

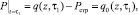(6)

т.е. часть нагрузки, равная величине структурной прочности сжатия Pстр [1], сразу же воспринимается скелетом грунта. Это означает, что любой грунт можно рассматривать как состоящий из отдельных структурных элементов, связанных между собой через контакты силами различной природы. При этом прочность самих структурных элементов намного выше прочности контактов между этими элементами. Поэтому прочность и другие свойства грунтов определяются в основном прочностью контактов.

Исследуемая задача консолидации неоднородных упругоползучих двухфазных грунтов при (1)–(6) выражениях сводится к решению интегро-дифференциального уравнения вида:

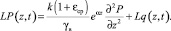(7)

Здесь

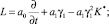
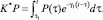
Решение уравнения (7), удовлетворяющее граничным (5) и начальному (6) условиям, можно представить в виде:

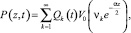(8)

где

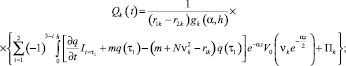(9)

здесь

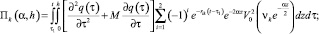
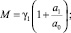
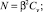
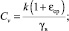
r1i, r2i – решение следующего квадратного уравнения

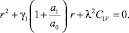
Функции 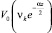, входящие в (8) и (9), имеют вид:

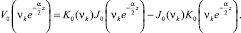(10)

Параметр νk является корнями трансцендентного уравнения вида

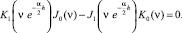(11)

Рассмотрим случай, когда q(z, t) = q = const, тогда давление в поровой жидкости из (8)–(11) вычисляется по следующей формуле:

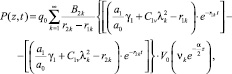(12)

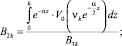
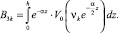где (13)

Напряжение в скелете грунта вычисляется по формуле:

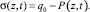(14)

Полученные выражения (12)–(14) соответственно позволяют определить изменения давления в поровой жидкости и напряжений в скелете грунта для любой точки рассматриваемой конечной области уплотнения неоднородного двухфазного грунта, обладающего упругим свойством. После того как определено напряжение в скелете уплотняемого неоднородного грунтового массива, можно вычислить и вертикальные перемещения точек верхней поверхности уплотняемого слоя грунта (осадок). Действительно, если к поверхности слоя грунта приложена некая вертикальная нагрузка, то соответствующая ей осадка s(t) может быть определена по формуле

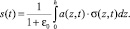(15)

Определим теперь осадку слоя неоднородного водонасыщенного глинистого грунта по формуле (15), т.е.

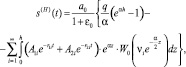(16)

где

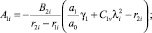
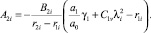
Из (16) при t → ∞ имеем

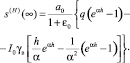(17)

В работе при помощи формул (12)–(17) произведены вычисления значений порового давления, напряжения в скелете грунта и осадок точек верхней поверхности уплотняемого грунтового массива. При этом одновременный учет ползучести и неоднородности уплотняемого грунта оказывает существенное влияние на напряженно-деформированное состояние грунтового основания сооружений. Количественное сравнение результатов значений осадок верхней поверхности уплотняемого грунтового массива в начальный момент времени говорит, что для неоднородного грунта они происходят интенсивнее, нежели для однородного уплотняемого массива. Эта разница после некоторого момента времени становится несущественной.

Библиографическая ссылка