Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Саитов В.Е. 1 Суворов А.Н. 1

---

1 ФГБНУ «НИИСХ Северо-Востока»

Отмечается, что эффективность производства зерна во многом зависит от совершенства технологий и технических средств, обеспечивающих качественную послеуборочную его обработку при наименьших затратах труда и средств, минимальных потерях зерна в отходы. При этом для прогнозирования потерь зерна в процессе работы зерноочистительных машин необходимо моделирование поведения зернового вороха в различных их рабочих органах. Для этого необходимо знание закона распределения компонентов зернового вороха по скоростям υвит. витания. Наиболее распространенным критерием проверки гипотезы о виде закона распределения является критерий χ2 (Пирсона). Алгоритм проверки данного критерия приводится в данной статье.

Статья в формате PDF

1047 KB

зерновой ворох

скорость витания частиц

критерий χ2 (Пирсона)

вариационный ряд

полигон частот

выборочная дисперсия

число степеней свободы

закон распределения компонентов зернового материала

число интервалов

1. Разработка и совершенствование малогабаритных пневмосепараторов с замкнутым циклом воздушного потока / В.Е. Саитов, В.Г. Фарафонов, А.Н Суворов, Д.В. Григорьев // Международный журнал экспериментального образования: Материалы XV Всероссийской выставки-презентации учебно-методических изданий из серии «Золотой фонд отечественной науки». – 2012. – № 11. – С. 38-39.

2. Саитов В.Е. Исследование процессов в рабочих органах сепараторов зерна / В.Е. Саитов, В.Г. Фарафонов, А.Н. Суворов // Международный журнал экспериментального образования: Материалы XV Всероссийской выставки-презентации учебно-методических изданий из серии «Золотой фонд отечественной науки». – 2012. – № 11. – С. 39-40.

3. Физико-математическое моделирование процессов разделения зерновых материалов для повышения эффективности функционирования зерно- и семяочистительных машин / В.Е. Саитов, В.Г. Фарафонов, А.Н. Суворов, С.В. Синяков // Международный журнал прикладных и фундаментальных исследований: Материалы XIV Всероссийской выставки-презентации учебно-методических изданий из серии «Золотой фонд отечественной науки». – 2012. – № 9. – С. 91-92.

4. Саитов, В.Е. Распределение компонентов зернового материала на решетке пневмоожижающего устройства / В.Е. Саитов, А.Н. Суворов // Тракторы и сельскохозяйственные машины. – 2011. – № 1. – С. 31-33.

5. Саитов, В.Е. Применение статистического метода к фракционированию легких отходов в осадочной камере / В.Е. Саитов, В.Г. Фарафонов, А.Н. Суворов // Тракторы и сельскохозяйственные машины. – 2011. – № 6. – С. 30-33.

6. Саитов, В.Е. Исследование процесса отделения примесей в криволинейном отводном канале жалюзийного воздухоочистителя / В.Е. Саитов, В.Г. Фарафонов, А.Н. Суворов // Механизация и электрификация сельского хозяйства. – 2012. – № 1. – С. 3-5.

7. Кремер, Н.Ш. Теория вероятностей и математическая статистика: учебник для вузов / Н.Ш. Кремер. – М.: ЮНИТИ-ДАНА, 2004. – 573 с.

8. Саитов, В.Е. Замкнутый малогабаритный пневматический сепаратор для очистки зерна / В.Е. Саитов, Д.В. Григорьев // Тракторы и сельскохозяйственные машины. – 2012. – № 7. – С. 15-18.

9. Пневмосепарирующее устройство зерноочистительной машины: пат. 2131784 Рос. Федерация: МПК6 В07В 4/02 / Сычугов Н.П., Саитов В.Е., Гатауллин Р.Г.; заявитель и патентообладатель Вятская гос. с.-х. академия. – № 97118588/03; заявл. 04.11.97; опубл. 20.06.99, Бюл. № 17. – 5 с.

10. Пневмосепарирующее устройство зерноочистительной машины: пат. 2150339 Рос. Федерация: МПК7 В07В 4/02 / Сычугов Н.П., Саитов В.Е., Гатауллин Р.Г.; заявитель и патентообладатель Вятская гос. с.-х. академия. – № 99105773/13; заявл. 17.03.99; опубл. 10.06.2000 Бюл. № 16. –5 с.

Одной из важных частей национальной безопасности любого государства, России в том числе, является продовольственная самодостаточность, которая зависит от степени развития сельского хозяйства. Важнейшей составляющей сельского хозяйства является производство зерновых культур. Повышение качества зерна во многом зависит от эффективности процессов послеуборочной обработки урожая [1, 2].

Эффективность производства зерна во многом зависит от совершенства технологий и технических средств, обеспечивающих качественную послеуборочную его обработку при наименьших затратах труда и средств, минимальных потерях зерна в отходы. При этом для прогнозирования потерь зерна в процессе работы зерноочистительных машин необходимо моделирование поведения зернового вороха в различных их рабочих органах.

Использование математического моделирования позволяет избежать значительных материальных и временных затрат, необходимых для постановки экспериментов, так как формализация связей между элементами модели позволяет выявить и устранить многие проблемы, которые могли бы повлиять на ход эксперимента [3, 4, 5, 6].

Алгоритм проверки гипотезы о виде распределения по критерию Пирсона

Для моделирования поведения зернового вороха в различных рабочих органах сельскохозяйственных машин с целью оптимизации их конструкционно-технологических параметров, прогнозирования потерь зерна при работе зерноочистительной машины необходимо знание закона распределения частиц зернового вороха по скоростям υвит. витания. Наиболее распространенным критерием проверки гипотезы о виде закона распределения компонентов зернового вороха является критерий χ2 (Пирсона). Проверка данного критерия осуществляется по следующему алгоритму:

1. По выборочным данным строится вариационный ряд. Для этого диапазон изменения исследуемой величины, в нашем случае скорости υвит. витания, разбивается на несколько промежутков. Число промежутков чаще определяется произвольно, например, промежутки одинаковой ширины 1 м/с, либо по формуле Стерджеса [7]

т = 1+3;322ln n, (1)

где n – число элементов выборки; т – рекомендуемое число интервалов.

В качестве значения исследуемой величины берутся середины полученных интервалов, а число точек, попавших в соответствующий интервал, обозначается пi и называется частностью. Причем, справедлива формула

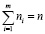. (2)

Если в какой-либо интервал попадает слишком мало значений (в статистике принято считать слишком малым ni < 5), то этот интервал необходимо объединить с одним или несколькими соседними интервалами так, чтобы в итоге каждый интервал содержал достаточное число значений.

2. По вариационному ряду строится полигон частот. По горизонтали откладываются значения величины, по вертикали частости. Иногда вместо частостей откладывают частоты, т.е. отношения ni/n. Полученные точки соединяются ломаной.

3. По внешнему виду полигона формулируется нулевая гипотеза о виде распределения Н0.

4. Определяются параметры гипотетического распределения как выборочные оценки. В случае гипотезы о нормальном распределении исследуемой величины в качестве параметров используются выборочное среднее и выборочное среднее квадратичное отклонение, определяемые по формулам [7]:

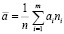, (3)

где 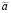– среднее значение исследуемой величины; аi – середина i-го интервала;

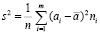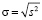, , (4)

где s2 – выборочная дисперсия; σ – выборочное среднее квадратическое отклонение.

5. Строится теоретическое распределение с найденными параметрами.

6. Определяется различие между теоретическим и эмпирическим законами распределения [7]:

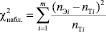, (5)

где nЭ(Т)i – эмпирические (теоретические) частности.

7. Оценивается значимость этого различия. Для этого определяется число степеней свободы

k=m–r–1, (6)

где k – число степеней свободы; r- число параметров, задающих закон распределения.

Для полученного числа степеней свободы и заранее заданного уровня значимости критерия по таблице находится критическое значение распределения 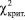. После этого производится оценка. Если 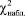<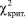, то различие между теоретическим и эмпирическим законом распределения незначимо, т.е. гипотеза Н0 принимается. В противном случае гипотеза Н0 отвергается.

Заключение

С учетом приведенного алгоритма проверки гипотезы о виде распределения по критерию χ2 (Пирсона) зерновой смеси пшеницы сорта Ирень, состоящей из 97 % полноценных зерен основной культуры, 2 % щуплых зерен основной культуры и 1 % сорных примесей, свидетельствует, что наблюдаемые значения критерия Пирсона χ2 набл.10 = 1,7657, χ2 набл.20 = 3,2574, χ2 набл.30 = 0,3891 меньше их табличных критических значений χ2 крит.10 = 3,84, χ2 крит.20 = 7,82, χ2 крит.30 = 3,84 для уровня значимости 0,05 и 1 степени свободы для полноценного зерна и сорных примесей и 3 степени свободы для щуплого зерна. Поэтому гипотеза о нормальном законе распределения полноценных зерен основной культуры, щуплых зерен основной культуры и сорных примесей принимается.

Полученные полигоны относительных частот компонентов данной зерновой смеси по скорости υвит. витания, их содержание и статистические параметры позволили сократить затраты на проведение экспериментов при создании замкнутого малогабаритного пневматического сепаратора [8] и проектировании зерноочистительных машин [9, 10].

Библиографическая ссылка