Для решения многих экономических задач используется сложный математический аппарат. В основном такие задачи сводятся к нахождению наибольшего или наименьшего значений (например, получение максимальной прибыли или нахождение минимальных издержек). Условие экономической задачи необходимо записать математически. Для этого вводим переменные. Исходя из цели задачи, составляем функцию, которая называется целевой, ограничения на переменные записываем в виде неравенств или уравнений.
Таким образом, приходим к нахождению наибольшего или наименьшего значения целевой функции. Так как число переменных больше одной, то при исследовании применяется функция нескольких переменных. Рассмотрим применение необходимого и достаточного условий функции двух переменных для нахождения наибольшего значения прибыли фирмы.
Пусть торговая фирма закупает товары двух видов в количестве х1 и х2 единиц. На основании опытных данных установлено, что доход фирмы в зависимости от х1 и х2 выражается функцией:
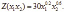
Она обладает следующими свойствами:
1) 
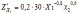
2) 
→ 
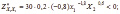
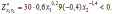
3) 
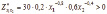
Так как ,
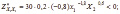
значит с увеличением товара, X1 его предельная полезность уменьшается. Графиком функции Z является некоторая поверхность пространства. Каждой точке поверхности соответствует определённое значение дохода, полученное при данном сочетании набора товаров .Получаем кривые плоскости, которые называются изоквантами.
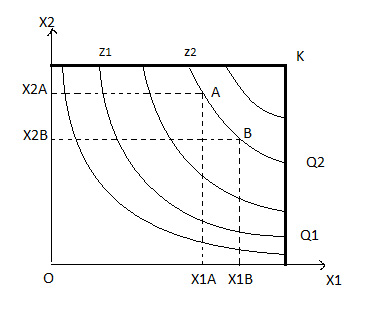
По изоквантам определяем, как один товар заменяется вторым. Рассмотрим замену одного товара другим аналитически: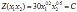 
Поделив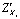 
на 
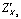получим: = 
.
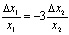Подводя итоги, можно сказать, что, повышая первый товар на 1%, второй уменьшается на 3%.
Пусть (р1, р2) - вектор цен за единицу товара, тогда прибыль фирмы будет выражена через функцию:
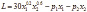
Торговая фирма обладает бюджетом J, тогда переменные х1 и х2 должны удовлетворять условию: р1 х1+р2х2=J
Используя необходимое условие существования экстремума для функции двух переменных и дополнительное ограничение, получим систему уравнения:
=> 
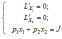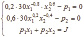
Разделим первое уравнение системы на второе и получим, что
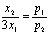
Из этого следует, что p1x1 + p13x1 =J, тогда х1=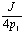
, x2=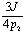
.
При J=100 000, p1=400, p2=200, найдем числовые значение х1 и х2
х1=62,5 х2=187,5
Вычислим, какую часть всего бюджета составляют товары значение х1 и х2
p1x1=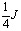
, p2x2=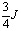
Подводя итог можно сказать, что при заданных ценах за единицу товара и бюджете, расходы на первый товар составляют ¼ ;а на второй товар ¾ всего бюджета.
Библиографическая ссылка
Горелова А.В., Семкина А.А., Фомин В.И. РАСЧЕТ ПРИБЫЛИ ТОРГОВОЙ ФИРМЫ С ПОМОЩЬЮ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ // Современные наукоемкие технологии. – 2014. – № 7-3. – С. 37-38;URL: https://top-technologies.ru/ru/article/view?id=34498 (дата обращения: 23.11.2024).