Процесс производства любого продукта связан с потреблением разнообразных ресурсов. В число ресурсов входит все, что требуется для производственной деятельности, - сырье и материалы, труд, энергия, оборудование и другое.
Зависимость количества продукта, которое может произвести фирма, от объемов затрат ресурсов получила название производственной функции.[1]
Производственную функцию можно построить как для отдельной фирмы или отрасли, так и в целом для всей национальной экономики.
В целях моделирования реальных производственных процессов на практике наиболее часто используют два вида таких функций: линейную и функцию Кобба-Дугласа.
Линейная производственная функция строится в тех случаях, когда величина затрат пропорциональна объему выпуска.
Функция Кобба — Дугласа показывает зависимость объёма производства от создающих его факторов производства — затрат труда и капитала.[2]
Общий вид функции: Q = A*La*Kb, где
А — технологический коэффициент;
a — коэффициент эластичности по труду;
b — коэффициент эластичности по капиталу.
Построение производственных функций позволяет:
1. Производить аналитические расчеты;
2. Оценивать эффективность использования и целесообразность дополнительного вовлечения ресурсов в производственный процесс;
3. Прогнозировать объем выпуска при различных вариантах развития объекта (то есть при различных количествах ресурсов).
Практический пример построения производственной функции.
Используя данные по производству электроэнергии, газа и воды в Сибирском Федеральном округе (см. рисунок 1) [3] построить производственную функцию, описывающую зависимость объема производства электроэнергии, газа и воды в Сибирском Федеральном округе от факторов «труд» и «капитал»:
Y = a0 * Ka1 * La2, где Y – объем производства электроэнергии, газа и воды; К – основные фонды;
L – трудовой фактор, численность промышленно-производственного персонала (ППП).
Для того, чтобы построить данную модель, необходимо для начала произвести линеаризацию переменных, для чего прологарифмируем обе части уравнения:
lnY = lna0 + a1lnK + a2lnL
В начальной (мультипликативной) модели a0 принимается равным единице. В литературе экономического содержания параметр a0 интерпретируется как коэффициент нейтрального технического прогресса. (Нейтральный технический прогресс определяется такими техническими изменениями, которые не нарушают равновесия, то есть экономически и социально «безопасны» для общества).[4]
Рассчитаем параметры регрессионной модели (см. рис 2).
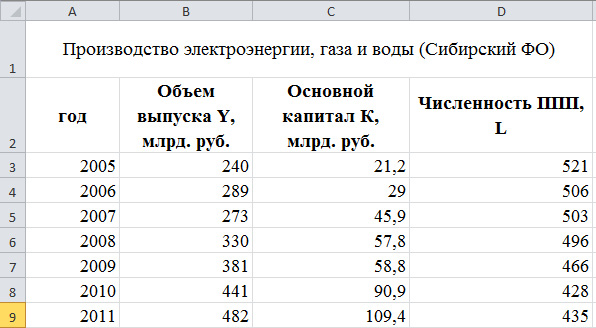
Рис. 1 Производство электроэнергии, газа и воды в Сибирском Федеральном округе
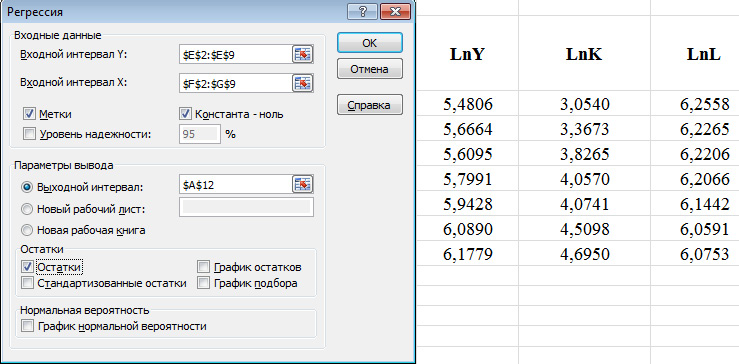
Рис. 2 Построение модели без свободного члена
Для решения этой задачи воспользуемся Анализом данных в Excel. В диалоговом окне Регрессия необходимо выставить флажок Константа – ноль.
В результате проведенного анализа получены следующие значения коэффициентов:
а1 = 0,495
а2 = 0,628
Таким образом, уравнение регрессии будет иметь следующий вид:
lnY = 0,495 lnK + 0,628 lnL
производственная функция при переходе к исходным данным:
Y = K0, 495 * L0, 628
Вывод:
Дадим экономическую интерпретацию параметров а1 и а2:
а1 – эластичность выпуска по основным фондам, она равна 0,495, то есть при увеличении фондов на 1% выпуск увеличится на 0,495%;
а2 – эластичность выпуска по труду, она равна 0,628, то есть при увеличении численности работников на 1% выпуск увеличится на 0,628%.
Так как а2 > а1, то можно сделать вывод о том, что в 2005-2011 гг. наблюдался фондосберегающий (экстенсивный) рост. Обратная ситуация характеризовалась бы как трудосберегающий (интенсивный) рост.
Библиографическая ссылка
Нан-Хоо О.С. ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ, ПРИМЕР ПОСТРОЕНИЯ // Современные наукоемкие технологии. 2014. № 7-3. С. 20-21;URL: https://top-technologies.ru/ru/article/view?id=34491 (дата обращения: 25.01.2026).



