Рассматриваются периодические движения вблизи треугольных точек либрации фотогравитационной задачи трех тел, отличающиеся от соответствующей классической задачи тем, что основные тела, обращающиеся по круговым орбитам, являются излучающими.
Найдены многопараметрические решения задачи вблизи треугольных точек либрации, отвечающих точным решениям соответствующей системы дифференциальных уравнений ограниченной фотогравитационной задачи трех тел.
Доказано, что возможные периодические движения являются плоскими, расположенными в плоскости орбитального движения основных тел.
Показано, что траектории движения частиц в окрестности исследуемых треугольных точек будут эллипсами, полуоси которых зависят от параметров фотогравитационного поля.
Как известно, периодические движения вблизи точек либрации классической ограниченной задачи трех тел исследованы многими авторами [1,2]. В работах [5,6] впервые сформулирована и доказана общая теорема о существовании ляпуновских семейств симметричных периодических движений и строго математически обоснован конструктивный метод численного построения и исследования их устойчивости в обратимой системе. Построение траекторий путем численного интегрирования системы уравнений, поиск симметричного периодического решения, а также способ исследования устойчивости орбиты вокруг коллинеарных точек либрации ограниченной фотогравитационной задачи трех тел успешно реализованы в работе [7].
Поставим задачу определения периодических движений вблизи треугольных точек либраци L4 и L5 ограниченной фотогравитационной круговой задачи, дифференциальные которой имеют вид
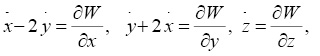
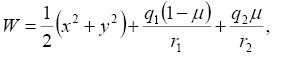
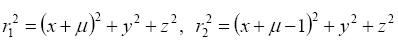(1)
Здесь 
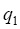и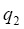 
– коэффициенты редукции, зависящие от мощности излучения основных тел и парусности частицы, определяемой отношением «сечение/масса», 
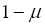и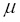 
- безразмерные массы основных тел.
Рассмотрим теперь решения системы уравнений (1), близкие к треугольным точкам. Для этого введем обозначения
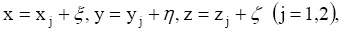
где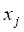 
, 
, 
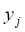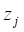- координаты треугольных точек, которые подставляя в (1), получим уравнения возмущенного движения относительно отклонений ξ, η и ζ, решения которых ищем в виде рядов, расположенных по степеням некоторой произвольной постоянной c коэффициентами, представляющими 2π-периодические функции времени. Применяя метод, предложенный А.М. Ляпуновым [1], запишем уравнения, определяющие первые коэффициенты искомых рядов
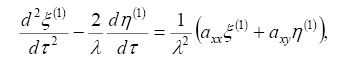
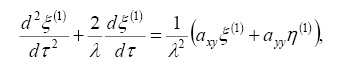
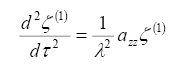(2)
Решение (2) ищем в виде
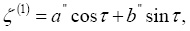
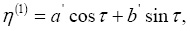
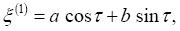
(3)
и для определения в них неизвестных коэффициентов подставим уравнения (3) в систему (2) и имеем
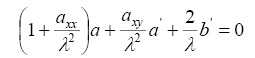
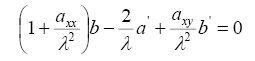
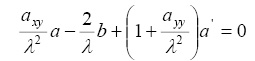
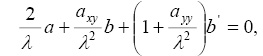
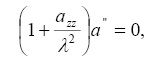
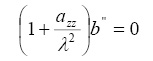. (4)
где
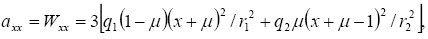
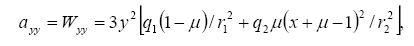
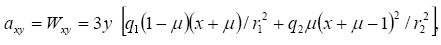
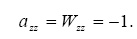
Первые четыре уравнения системы (4) перепишем в виде
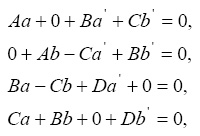(5)
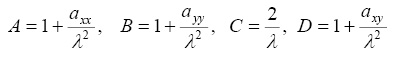
Определители системы (5) и двух последних уравнений (4) имеют вид:
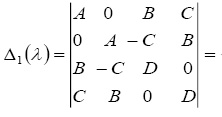
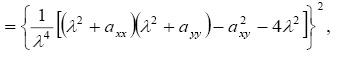(6)
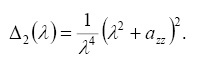
Характеристическое уравнение исследуемой системы распадается на два уравнения:
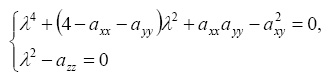(7)
Первое из (7) имеет две пары чисто мнимых корней при выполнении условий
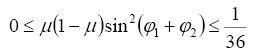,(8)
где 
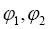и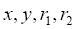 
между собой связаны следующими выражениями [8]:
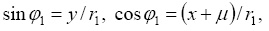
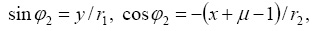
Корни характеристического уравнения, соответствующего первому из (7), могут быть записаны как [4]
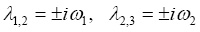, где
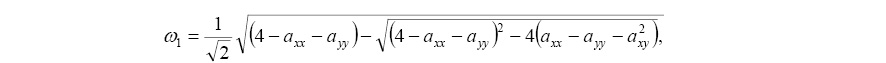
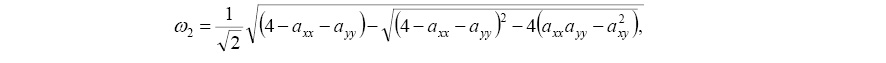
С учетом (7) и (9) нетрудно установить, что определители системы (4) относительно коэффициентов равны
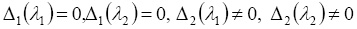(10)
Теперь легко установить, что система первых четырех уравнений системы (4) имеет решения, в которых все искомые величины не равны одновременно нулю, а два её последних уравнения имеют только тривиальное решение. Поэтому функция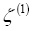 
равна нулю тождественно, а так как всякая функция Z(k) имеет множители 
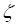, то любая 
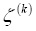равна тождественно нулю, т.е.
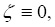(11)
и, следовательно рассматриваемое периодическое решение – плоское.
Таким образом, коэффициенты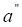 
и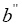 
равны нулю. Чтобы найт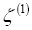и 
и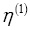 
нужно определить постоянные a, b, a΄, b΄ из системы уравнений (4).
Элементарный анализ этих уравнений позволяет получить, что
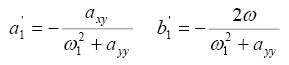
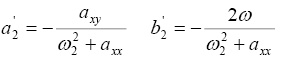(12)
Первые два периодических решения системы определяются формулами
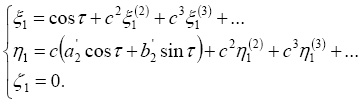(13)
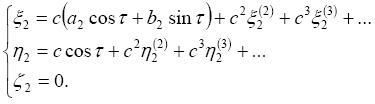(14)
Ограничиваясь только членами первого порядка относительно с в уравнениях (13) и (14), получим
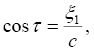
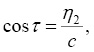
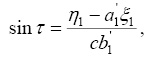
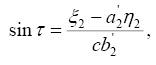
где
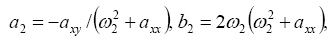
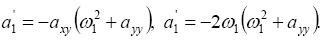
а c – произвольный параметр, в качестве которого может быть принято начальное отклонение, например, величины ξ.
Уравнения орбит, соответствующих каждому из решений (10) и (11), приближенно могут быть записаны в виде
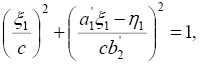
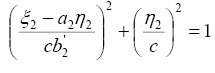(15)
Как видим, каждое из уравнений (15) представляет уравнение эллипса с центром, расположенным в области семейства устойчивых треугольных точек либрации. Следовательно, найденным периодическим решениям соответствует трехпараметрическое семейство замкнутых эллиптических орбит, окружающих треугольные точки и расположенные в плоскости орбитального движения, которые сохраняют свои формы во вращающейся вместе с основными телами системе координат, а их размеры зависят от интенсивности излучения основных тел и парусности частицы. Функции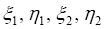 
будут периодическими функциями времени с периодами
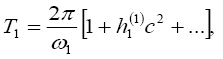
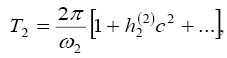
Рассматриваемая задача является наиболее важной с точки зрения приложений в звездной динамике: на её основе можно эффективно строить промежуточные орбиты космических газопылевых облаков в поле двойных звездных систем. Результаты исследования также могут быть использованы и при изучении движения космических аппаратов в системе «Солнце-Планета».
Библиографическая ссылка
Турешбаев А.Т., Омарова У.Ш., Бексейтова А.Б. ПЕРИОДИЧЕСКИЕ ДВИЖЕНИЯ В ОКРЕСТНОСТИ ТРЕУГОЛЬНЫХ ТОЧЕК ЗАДАЧИ ТРЕХ ТЕЛ С ИЗЛУЧАЮЩИМИ МАССАМИ // Современные наукоемкие технологии. 2014. № 3. С. 162-164;URL: https://top-technologies.ru/ru/article/view?id=34142 (дата обращения: 03.04.2025).