Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Зайкин О.А. 1 Шеховцов В.В. 2

---

1 ФГБОУ ВПО «Астраханский государственный технический университет»

2 ФГБОУ ВПО «Волгоградский государственный технический университет»

По анализу результатов теоретических расчетов и экспериментальных исследований моделей, изготовленных по четырем схемам зубчатых дифференциалов, формирующих точную прямолинейную траекторию без направляющей и шатуна, было определено, что, при округления числа зубьев любого колеса в конструкции, прямая траектория вырождается в устойчивую гипоциклоиду. Это ведет к заклиниванию механизма. Поэтому, задача точного проектирования чисел зубьев решалась комплексно. Для замыкающей ступени предложен стандартный метод разложения на сомножители передаточного числа. Для пары сателлит – центральное колесо, разработан табличный метод подбора чисел зубьев по коэффициентам кратности модулю.

Статья в формате PDF

395 KB

дифференциал

гипоциклоида

число зубьев

модуль.

1. Зайкин О.А. Проектирование малогабаритных двигателей и компрессоров с точным поступательным движением поршней без направляющей на основе схем замкнутых дифференциалов // Вестник АГТУ. Сер.: Машиностроение 2005. № 2 (25). – Астрахань: Изд-во АГТУ, 2005. – С.44-50.

2. Зайкин О.А. Синтез дифференциальных зубчатых механизмов с точным прямолинейным движением без направляющей для проектирования малогабаритных поршневых агрегатов и устройств // Проблемы механики современных машин: сб. ст. Пятой междун. конф. (Улан-Уде, 25-30 июн. 2012 г.). – Улан-Уде, 2012. – Т.1. – 276 с. – С.52-55.

Введение

Разработка инженерной методики расчета механизмов с кинематическим принципом организации точного прямолинейного движения имеет сложность в подборе размеров звеньев, связанную с соблюдением точности кинематических условий.

Рассмотрим проблемы проектирования бесшатунных зубчатых замкнутых дифференциалов с точным прямолинейным движением, разработанных автором для приводов транспортно-технологических машин [1].

Передаточное число замыкающей ступени замкнутого дифференциала U2Н =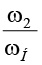

(2 – центральное колесо, Н – водило) обеспечивает необходимую скорость в полюсе зацепления сателлита и центрального колеса, при которой формируются мнимые образующие окружности R = 2e и r = e, обеспечивающие кинематику точного прямолинейного движения в схеме [2]. Кроме того, числа зубьев z1 – сателлита и z2 – центрального колеса образуют радиусы, по которым рассчитывают величину U2Н.

Теоретические исследования по влиянию точности подбора чисел зубьев звеньев дифференциала, и эксперименты с моделями показали, что при округлении чисел зубьев при их подборе в соответствии с модулем, прямая траектория вырождается в гипоциклоиду (рис.1), даже при разнице в один зуб.

По этой причине методика должна обеспечивать расчет чисел зубьев всех колес абсолютно точно без округлений совместно с подбором модуля в нескольких вариантах.

Цель исследования – разработка методики расчета чисел зубьев колес зубчатого бесшатунного дифференциала, формирующего точное прямолинейное движение, в которой обеспечивается стабильность существования прямолинейности траектории.

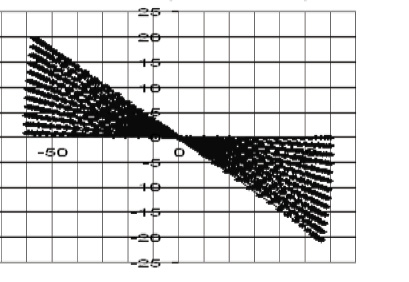
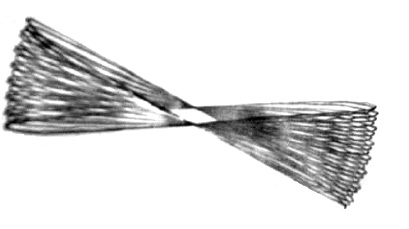
Рис. 1. Расчетная и экспериментальная бабочка гипоциклоиды
за 12 циклов при корректировке на один зуб

Содержание исследования

Для решения задачи точности в замыкающей ступени применяем известный метод разложения передаточного числа на сомножители. В общем случае, для блочной схемы имеем:

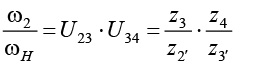
где z2' – число зубьев замыкающего зубчатого венца центрального колеса;

z3’ и z3 – число зубьев промежуточного блока замыкающей ступени;

z4 – число зубьев дополнительного зубчатого колеса на водиле.

Единственное требование – число U2Н не должно быть периодическим.

Более сложной задачей является подбор чисел зубьев колес зацепления (z1 –z2)– сателлита и центрального колеса дифференциала. Основным усложняющим фактором является то, что радиусы колес уже сформированы приращением Δ и эксцентриситетом дифференциала е:

R1 = e + ∆ и R2 = 2e + ∆.

Величина эксцентриситета задается технологическим ходом поступательного движения 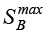и равна – е = 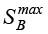/4.

В соответствии с выражением – d = 2R = mz имеем зависимости чисел зубьев:

и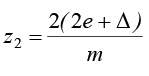  

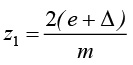
Из выражения для z1 , следует, что целым числом z1 может быть как при целых, так и при дробных е и ∆, но в сумме кратных выбранному модулю. Однако, из выражения для z2 следует, что величины 2е и ∆, каждая должны быть кратными модулю.

Решение поставленной задачи имеет два варианта:

1. Обеспечить сохранность R1 = e + ∆ и R2 = 2e + ∆, применив колеса, нарезанные со смещением. Недостатком этого решения является одновариантность решения и, из-за использования исправленных зубчатых колес, а, следовательно, низкая ремонтопригодность.

2. Обеспечить, чтобы z1 и z2 были целыми числами, при их расчете, без округлений. Решением задачи подбора чисел зубьев z1 и z2 по второму варианту является определение коэффициента кратности модулю. Как уже было отмечено, модуль должен быть кратным и 2е и е и ∆. Но не все стандартные модули являются целыми числами, поэтому для нахождения коэффициентов кратности разложим оба их ряда на сомножители. Так как модуль расположен в знаменателе выражения, то числитель разложенной дроби модуля и будет коэффициентом кратности для расчета числа зубьев (таблицы 1 и 2).

Сгруппируем модули по коэффициентам кратности в таблице 3, а с учетом повторяемости.

Сформируем таблицу 4 по коэффициентам кратности так, чтобы при значении диапазона 40 мм < 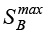< 240 мм (с учетом хода в типовых поршневых агрегатах), по ним можно было выбрать значение 2е, е и ∆ с кратностью по модулю. В строке названий колонок – слева число, а справа – коэффициент кратности для этих чисел.

Таблица 1

I ряд модулей

Таблица 2

II ряд модулей

Таблица 3

Группы модулей по коэффициентам кратности

Методика работы с таблицами следующая:

1. По 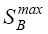рассчитаем 2е, е примем конструктивно требуемый ∆, в диапазоне 0 < ∆ < 2е. Знак у ∆ берется по модулю.

2. По табл. 4 выбираем варианты коэффициентов кратности для 2е, е и ∆.

3. По табл. 3 выбирают варианты модуля для расчета z1 и z2 .

4. Принимают числа зубьев, соблюдая условия: z1 ≥ zмин = 17 и z2 ≥ 28 Окончательно числа зубьев определяет минимизация размеров и условие прочности зуба.

Результаты исследования

Рассмотрим применение таблиц при решении конкретных задач:

Пример: Подберем числа зубьев для среднего хода поршневых машин. Примем поступательный ход – 100мм. Тогда е = 25мм и 2е = 50мм. Из таблицы 4 выбираем варианты коэффициента кратности – k = 5. Варианты приращение ∆ = 10, 15, 20, 25мм. Из таблицы 3 берем варианты модулей при кратности 5 – m = 1,25; 2,5; 5.

Таблица 4

Выбор 2е, е, ∆ и m
по коэффициенту кратности

Числа зубьев соответственно равны:

m = 1,25

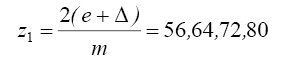
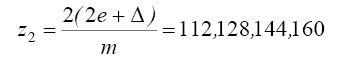
m = 2,5

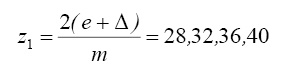
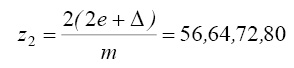
m = 5

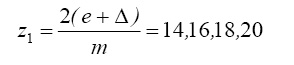
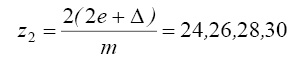
Оптимальными могут быть варианты: z1 = 18 и z2 = 28 при m = 5 мм, или – z1 = 28 и z2 = 56 при m = 2,5 мм, или z1 = 56 и z2 = 112 при m = 1,25 мм.

Безусловно, простым подбором никогда не предугадать этих вариантов. Аналогично можно рассчитать параметры колес при любых исходных данных, а величину ∆ можно принимать разной величины.

При работе с таблицами 4 надо учесть, что в верхнем блоке выбираются только е и ∆, для которых 2е выбирается из второго блока. Если же е и ∆ берутся из второго блока, то 2е принимается из третьего блока.

Выводы

Таким образом, разработана простая методика решения задачи проектирования размеров зубчатых колес замкнутых дифференциалов с точным прямолинейным движением по заданному ходу табличным способом, с возможностью инвариантного принятия решения о конечном наборе. При этом, абсолютно точно сохранена теоретическая прямолинейность движения в проектируемых механизмах.

Библиографическая ссылка