Известно, что автоматический процесс описывается линейным неоднородным дифференциальным уравнением второго порядка:
у”+р(х)у’+q(x)y=f(x) (1)
Частные решения этого дифференциального уравнения: у1=1, у2=х, у3=х2.
Необходимо найти общее решение этого дифференциального уравнения.
При подстановке: у1=1, у2=х, у3=х2 уравнение (1) обращается в тождество. Получаем систему:
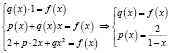
Исходное дифференциальное уравнение с найденными величинами запишется:
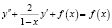 ,
,
у″+у′ =0,
y″+py′=0.
Понизим порядок этого дифференциального уравнения, введя замену у′=V, где V=V(x).
Получим дифференциальное уравнение первого порядка с разделяющимися переменными:
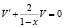 .
.
Его решением является функция: V=C1(x–1)2 или у′=С1(х–1)2.
Окончательно получаем:
y=D1(x–1)3+D2.
Библиографическая ссылка
Светличная В.Б., Мальцев А.В., Рубцов А.А. ПОИСК ОБЩЕГО РЕШЕНИЯ ЛИНЕЙНОГО НЕОДНОРОДНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПО ИЗВЕСТНЫМ ЧАСТНЫМ РЕШЕНИЯМ // Современные наукоемкие технологии. 2014. № 5-2. С. 199-200;URL: https://top-technologies.ru/ru/article/view?id=34071 (дата обращения: 05.03.2026).



