Когда вид связи между параметрами x и y неизвестен, наиболее распространённым случаем, является задание этой связи в виде некоторой таблицы (табл. 1).
Таблица 1
|
x |
x1 |
x2 |
… |
xn |
|
y |
y1 |
y2 |
… |
yn |
Эти значения – либо экспериментальные данные, либо результаты расчётов. На практике могут понадобиться значения величины y и в других точках, отличных от узлов xi. Однако получить эти значения можно лишь путём очень сложных расчётов или проведением дорогостоящих экспериментов.
С точки зрения экономии времени и средств необходимо использовать табличные данные для приближённого вычисления искомого параметра y при любом значении параметра x (из некоторой области), поскольку точная связь не известна. Этой цели служит задача о точечной аппроксимации – интерполяции. Она состоит в нахождении функции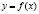 
, проходящей через заданные точки (узлы интерполяции).
На практике, в качестве интерполяционных многочленов часто используются сплайны третьей степени, имеющие на отрезке [a, b] непрерывную, по крайней мере, первую производную. Такие сплайны называются кубическими и обозначаются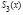 
.
Пусть на отрезке [a, b] заданы значения некоторой функции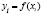 
, 
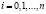. Интерполяционным кубическим сплайном называется сплайн вида:
,
,
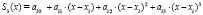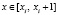удовлетворяющий условиям:
а) функция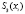 
непрерывна вместе со своими производными до второго порядка включительно;
б)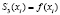 
, 
;
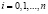в)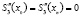 
.
В результате применения метода к данным таблицы, получается системы линейных алгебраических уравнений, имеющая трёхдиагональную матрицу с диагональным преобладанием. Такие матрицы являются неособенными. Поэтому решение системы существует и притом единственное. Для нахождения неизвестных используется метод прогонки.
Решение задачи построения кубического сплайна осуществлялось в системе Mathcad 13.
В качестве примера выбраны данные:
, 
.
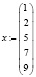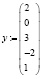В результате реализации получен сплайн, изображённый на рис. 1 вместе с исходными данными. Построенный сплайн проходит через узлы интерполяции.
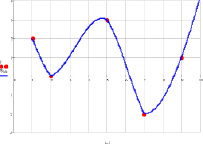
Рис. 1
Кубическая сплайн-функция обладает наименьшей (в некотором смысле) кривизной среди всех дважды непрерывно дифференцируемых функций на данном отрезке [a, b] с заданными значениями в узлах интерполяции.
Библиографическая ссылка
Алешин И.Ю., Сычева А.В, Агишева Д.К., Матвеева Т.А. ИНТЕРПОЛЯЦИЯ НЕИЗВЕСТНЫХ ФУНКЦИЙ КУБИЧЕСКИМИ СПЛАЙНАМИ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 188-189;URL: https://top-technologies.ru/ru/article/view?id=34060 (дата обращения: 22.11.2024).