Является ли разрешимое произведение упорядочиваемых групп упорядочиваемой группой. Оказалось, что разрешимое произведение упорядочиваемых групп вовсе не обязано быть упорядочиваемым. Контрпример строится для случая двуступенно разрешимого произведения упорядочиваемых групп.
Пусть A группа с образующими a,b,c и определяющими отношениями: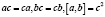 
A является упорядочиваемой группой. Обозначив через 
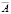фактор – группу 
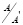группы A по её коммутанту A1, через 
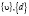бесконечные циклические группы и 
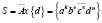, где k,e,n целые числа, e=0 или I. Построим группу 
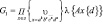со следующими соотношениями:
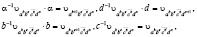
где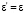 
группа G1 без кручения, причем, подгруппа ее 
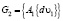является двуступенно разрешимой и 
.
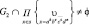В самом деле,
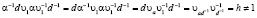
Существенным является то, что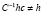 
, так
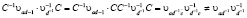
Далее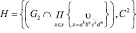 
инвариантная абелева подгруппа группы 
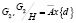абелева группа.
Возьмем группу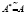 
и бесконечную циклическую группу {d*}. Тогда отображение 
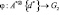при котором 
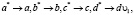где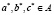 
можно продолжить до гомоморфизма, так как если некоторое слово равно единице в 
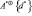, то образ этого слова равен единице в G2. Здесь символ 
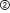обозначает двуступенно разрешимое произведение. Но в силу того, что C действует нетождественно 
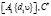действует нетождественно на 
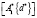Получается, таким образом, что 
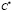индуцирует автоморфизм второго порядка на группе 
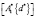и, следовательно, группа 
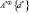не является упорядочиваемой, действительно, полагая 
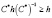получаем:
,
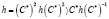а это недопустимо.
Таким образом, класс упорядочиваемых групп незамкнут относительно разрешимых произведений.
Библиографическая ссылка
Мамаев И.И., Светличная Е.Ю. ДВУСТУПЕННО РАЗРЕШИМОЕ ПРОИЗВЕДЕНИЕ УПОРЯДОЧИВАЕМЫХ ГРУПП // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 164-165;URL: https://top-technologies.ru/ru/article/view?id=34044 (дата обращения: 22.11.2024).