Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Иванов В.В. 1 Таланов В.М. 1

---

1 Южно-Российский государственный технический университет

Обсуждается вариант представления основных классов структурных состояний локальной транзитивной области в структурированном 2D пространстве.

Статья в формате PDF

863 KB

модулярная 2D P-ячейка

структурное состояние

локальная транзитивная область

1. Лорд Э.Э., Маккей А.Л., Ранганатан С. Новая геометрия для новых материалов. – М.: ФИЗМАТЛИТ, 2010. – 264 с.

2. Стюарт Я. Концепции современной математики. / Пер. с англ. Н.И. Плужниковой и Г.М. Цукерман – Мн: Выш. школа, 1980. – 384 с.

3. Иванов В.В., Таланов В.М. // Успехи соврем. естествознания, 2013. – № .7 – С. 74-77.

4. Иванов В.В., Таланов В.М. // Успехи соврем. естествознания, 2013. – № .6 – С. 61-63.

5. Иванов В.В., Таланов В.М. // Успехи соврем. естествознания, 2013. – № .7 – С. 78-81.

6. Иванов В.В., Таланов В.М. // Успехи соврем. естествознания, 2013 – № .6 – С. 64-67.

7. Иванов В.В., Таланов В.М. // Успехи соврем. естествознания, 2013. – № .6 – С. 68-72.

8. Иванов В.В., Таланов В.М. // Успехи соврем. естествознания, 2012. – № 8. – С. 75-77.

9. Иванов В.В., Таланов В.М. // Успехи соврем. естествознания, 2012. – № 10. – С. 78-80.

10. Иванов В.В., Таланов В.М. // Успехи соврем. естествознания, 2012. – № 9. – С. 74-77.

11. Иванов В.В., Таланов В.М. // Успехи соврем. естествознания, 2012. – № 3. – С.56-57.

12. Иванов В.В., Демьян В.В., Таланов В.М. // Успехи соврем. естествознания, 2012. – № 4. – С. 230-232.

13. Иванов В.В., Таланов В.М // Успехи соврем. естествознания, 2012. – № 11. – С. 61-62.

14. Иванов В.В., Таланов В.М. // Соврем. наукоемкие технологии, 2012. – № 11. – С. 24-25.

15. Иванов В.В., Таланов В.М. // Успехи соврем. естествознания, 2012. – № 11. – С. 63-65.

16. Иванов В.В., Таланов В.М. // Кристаллография, 2013. – Т. 58. – № 3. – С. 370–379.

17. Иванов В.В. Комбинаторное моделирование вероятных структур неорганических веществ. – Ростов-на-Дону: Изд-во СКНЦ ВШ, 2003. – 204 с.

18. Иванов В.В., Таланов В.М. // Кристаллография, 2010. – Т.55. – № 3. – С.385-398.

19. Иванов В.В., Таланов В.М. // Журн. неорганической химии, 2010. – Т.55. – № 6. – С.980-990.

20. Иванов В.В., Таланов В.М. // Физика и химия стекла, 2008. – Т.34. – № 4. – С.528-567.

21. Иванов В.В., Шабельская Н.П., Таланов В.М., Попов В.П. // Успехи соврем. естествознания, 2012. – № 2. – С.60-63.

22. Иванов В.В., Шабельская Н.П., Таланов В.М. // Соврем. наукоемкие технологии, 2010. – № 10. – С. 176-179.

23. Иванов В.В. // Соврем. наукоемкие технологии. 2013.- № .5. – С. 29-31.

24. Иванов В.В. // Успехи соврем. естествознания, 2013. – № 8. – С. 136-137.

25. Иванов В.В. // Успехи соврем. естествознания, 2013. – № 8. – С. 134-135.

26. Иванов В.В. // Успехи соврем. естествознания, 2013. – № 8. – С. 129-130.

27. Иванов В.В., Таланов В.М. // Наносистемы: Физика, Химия, Математика, 2010. – Т.1. – № 1. – С.72-107.

28. Иванов В.В., Таланов В.М., Гусаров В.В. // Наносистемы: Физика, Химия, Математика, 2012. Т.3. № 4. С.82-100.

29. Иванов В.В., Таланов В.М. / Журн. структурн. химии, 2013. Т.54. № 2. С.354-376.

30. Иванов В.В.. Ерейская Г.П., Люцедарский В.А. // Изв. АН СССР. Неорган. материалы, 1990. – Т.26, № 4. – С. 781-784.

31. Иванов В.В.. Ерейская Г.П, // Изв. АН СССР. Неорган. материалы. – 1991. – Т.27, № 12. – С. 2690-2691.

32. Иванов В.В., Таланов В.М. // Журн. структурн. химии. – 1992. – Т.33, № 3. – С. 137-140.

33. Иванов В.В., Таланов В.М. // Журн. структурн. химии. – 1992. – Т.33, № 5. – С. 96-102.

34. Иванов В.В., Таланов В.М. //Изв. вузов Сев.-Кавк. регион. Естеств. науки. – 1995. – № 2. – С. 38-43.

35. Иванов В.В., Таланов В.М. // Неорган. материалы. – 1995. – Т.31, N2. – С. 258-261.

36. Иванов В.В. // Изв. вузов. Сев.-Кавк. регион. Естеств. науки. – 1996. – № 1. – С. 67-73.

37. Иванов В.В., Щербаков И.Н. Моделирование композиционных никель-фосфорных покрытий с антифрикционными свойствами. – Ростов н/Д: Изд-во журн. «Изв. вузов. Сев.-Кавк. регион», 2006. 112 с.

38. Щербаков И.Н., Иванов В.В., Логинов В.Т. и др. Химическое наноконструирование композиционных материалов и покрытий с антифрикционными свойствами. – Ростов н/Д: Изд-во журн. «Изв. вузов. Сев.-Кавк. регион. Техн. науки», 2011. – 132 с.

39. Иванов В.В., Иванов А.В., Щербаков И.Н., Башкиров О.М. // Изв. вузов. Сев-Кавк. регион. Техн. науки. 2005. № 3. С.46-49.

40. Иванов В.В., Щербаков И.Н., Иванов А.В., Башкиров О.М. // Изв. вузов. Сев-Кавк. регион. Техн. науки. 2005. № 4. С.62-64.

41. Ivanov V.V., Balakai V.I., Ivanov A.V., Arzumanova A.V. // Russian Journal of Applied Chemistry. 2006. Т.79. № 4. С.610-613.

42. Ivanov V.V., Balakai V.I., Kurnakova N.Yu., Arzumanova A.V., Balakai I.V., // Russian Journal of Applied Chemistry. 2008. Т.81. № 12. С. 2169-2171.

43. Balakai V.I., Ivanov V.V., Balakai I.V., Arzumanova A.V. // Russian Journal of Applied Chemistry. 2009. Т.82. № .5. С.851-856.

44. Щербаков И.Н., Иванов В.В. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. 2011. № 5. С.47-50.

45. Дерлугян П.Д., Иванов В.В., Иванова И.В. и др. // Соврем. наукоемкие технологии. 2013. – № .5. – С. 21-24.

46. Ivanov V.V., Talanov V.M., Shabel’skaya N.P. // Inorganic Materials. 2001. Т.37. № 8. С.839-845.

47. Bespalova Zh.I., Ivanov V.V., Smirnitskaya I.V., et al. // Russian Journal of Applied Chemistry. 2010. Т.83. № 2. С. 242-246.

48. Ivanov V.V., Bespalova Zh.I., Smirnitskaya I.V., et al. // Russian Journal of Applied Chemistry. 2010. Т.83. № 5. С. 831-834.

Для решения задачи о представлении основных классов возможных структурных состояний локальной транзитивной области в структурированном 2D пространстве будем исходить из следующих предположений.

1. Транзитивная область 2D пространства – результат локального проявления вполне определенных структурных элементов 2D ячейки одного из подпространств 3D пространства, по аналогии с гипотетическим проявлением структурных элементов гиперпространства в 3D пространстве [1-7].

2. Структурное состояние транзитивной области может быть обусловлено как кристаллическими компонентами r подструктуры R2 структуры R3, так и ее возможными фрактальными компонентами f [8-16].

3. Кристаллическая компонента r модулярной структуры R2 в структурированном (ячеистом) 2D пространстве может быть определена как с помощью дискретной группы трансляций {ti}, так и с помощью непрерывной группы трансляций {τi} (i = 1, 2) [8-10, 17-22].

4. Фрактальная компонента f структуры R2 в структурированном 2D пространстве может быть определена как i-модулярная гибридная структура (в общем случае i = 1, 2) с помощью соответствующих своих генераторов (точечных, линейчатых или их возможных комбинаций) [23-29].

Многообразие вариантов сочетания кристаллической и фрактальной компонент возможных структурных состояний определяется количеством разновидностей определенных подструктур R2 структуры R3.

Число разновидностей 1D подструктур R11r и R11f в соответствующих R3 структурах может быть определено по формулам:

R33r = (Π3i=2 Cii-1) R11r = 6 R11r

R32r1f = 2 (Π2i=1 C2i) R11r + (Π2i=1 C2i) R11f = 4 R11r + 2 R11f

R31r2f = (Π2i=1 C2i) R11r + 2 (Π2i=1 C2i) R11f = 2 R11r + 4 R11f

R33f = (Π3i=2 Cii-1) R11f = 6 R11f

Аналогично, количество разновидностей 2D подструктур в соответствующих R3 структурах может быть определено по следующим формулам:

R33r = (Π3i=2 C3i) R22r = 3 R22r

R32r1f = (Π3i=2 Cii) R22r + 2 (Π3i=2 Cii) R21r1f = R22r + 2 R21r1f

R31r2f = 2 (Π3i=2 Cii) R21r1f + (Π3i=2 Cii) R22f = 2 R21r1f + R22f;

R33f = (Π3i=2 C3i) R22f = 3 R22f.

В соответствии с результатами последнего разложения гипотетической R3 структуры на R2 подструктуры проанализируем их вероятные структурные состояния с учетом кристаллической и фрактальной компонент или их возможных сочетаний (табл. 1).

Таблица 1

Возможные структурные состояния R2 подструктур соответствующей R3 структуры

Примечание. r – кристаллическая, а f – фрактальная компоненты структурного состояния.

С учетом характера элементов группы трансляций ячеистого 3D пространства, а также возможных топологических размерностей модулей фрактальных структур получены основные классы вероятных структурных состояний локальной транзитивной области структурированного 2D пространства (табл. 2).

Таблица 2

Основные классы структурных состояний локальной транзитивной области структурированного 2D пространства

Примечание. r и f – кристаллическая и фрактальная компоненты структурного состояния; t и t – дискретная и непрерывная трансляции как виды реализации генератора кристаллической компоненты.

Условные изображения ячеек для девяти классов структурных состояний локальной транзитивной области структурированного 3D пространства приведены на рисунке.

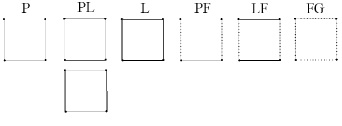
Условные изображения и обозначения квадратных ячеек разных классов структурных состояний локальной транзитивной области структурированного 2D пространства (символы: P – точечный, L – линейчатый, F – фрактальный, G – гибридный)

Необходимо отметить, что класс фрактальных гибридных структурных состояний FG в зависимости от вида генератора фрактала в свою очередь состоит из следующих подклассов: фрактальный точечный гибридный (FGр), фрактальный точечно-линейчатый гибридный (FGpl) и фрактальный линейчатый гибридный (FGl).

По своим индивидуальным геометрико-топологическим характеристикам и размерности транзитивные области разных классов существенно отличаются между собой. Очевидным образом это проявляется в локальных размерностях транзитивной области 2D пространства с разными классами структурными состояниями и разновидностями R2 структур. Если принять во внимание следующее: DimL R22r = Σ2i DimL R1ri , DimL R1t = 0, DimL R1t = 1, DimL R1f = DimL Gen R1f , то локальные размерности транзитивных областей 2D пространства со всеми возможными структурными состояниями могут быть определены (табл. 3).

Таблица 3

Локальные размерности транзитивных областей ячеистого 2D пространства

Следует отметить, что глобальная размерность структур только с кристаллической компонентой состояния DimG R22r = 2. Однако, если присутствует хотя бы одна фрактальная компонента состояния структуры, то тогда глобальная размерность ее DimG R22r < 2.

Таким образом, проанализированы основные классы структурных состояний локальной транзитивной области в структурированном 2D пространстве, представлено символьное описание состояний структур R2 и определены их локальные и глобальные размерности. Полученные данные о вероятных структурных состояниях без фрактальной составляющей использованы при интерпретации некоторых особенностей строения модулярных полигональных и полиэдрических R22r структур (как фрагментов R33r модулярных структур) [30-36]. Данные о структурных состояниях с фрактальной составляющей в 2D пространстве рассматривались как возможные аппроксиманты конфигураций межфазных границ и распределения фаз на поверхности антифрикционных композиционных материалов и покрытий в процессе их формирования и последующего трибовоздейстия [37-45], химически активных материалов и анодных покрытий [46-48].

Результаты работы получены при поддержке Минобрнауки РФ в рамках государственного задания на проведение НИОКР, шифр заявки N6.8604.2013.

Библиографическая ссылка