Проблема прогноза напряжений при нанесении защитных покрытий представляет собой практический интерес с точки зрения оптимизации их свойств [2, 3]. Настоящая работа посвящена математической формализации этого процесса.
Современные представления о физике нанесения плазменных газотермических покрытий можно сформулировать следующим образом. Поток расплавленных частиц напыляемого материала с некоторой скоростью сталкиваются с подложкой, и вступает с ней в физико-химическое взаимодействие. При этом происходит их быстрое охлаждение, сопровождающееся фазовыми превращениями. Это приводит к изменению линейных размеров и объема частиц.
В результате теплообмена основного изделия с окружающей средой, струей разогретого газа (плазмы) и частицами напыляемого материала происходит изменение объема и линейных размеров уже напыленного покрытия и подложки. В результате в слоях покрытия и подложке возникает система напряжений, которая может привести к тому, что при достижении некоторой критической комбинации произойдет либо отслоение, либо растрескивание покрытия [1, 4, 5].
При математической формализации процесса плазменного напыления нами были приняты следующие допущения:
– каждый напыленный слой покрытия рассматривается как квазиоднофазная среда, характеризующаяся некоторым уравнением состояния;
– между покрытием и подложкой, а также между соседними слоями напыляемого материала известны условия термомеханического контакта;
– плазмотрон (горелка) перемещается дискретно, при этом происходит практически мгновенное отверждение напыляемого материала;
– известны условия теплообмена основного изделия с окружающей средой и струей плазмотрона (горелки).
Таким образом, принятые допущения приводят к рассмотрению задачи сращивания в некоторый момент времени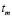 
двух тел, характеризующихся, в принципе, различными уравнениями состояния, температурой, напряжениями и деформациями.
Задача формируется следующим образом. Имеются два тела, занимающие области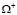 
(основное изделие с напыленным покрытием при 
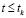) и 
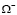(участок покрытия, напыленный при 
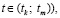которые при 
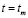вступают во взаимодействие. При этом предполагается, что при t < tk имеем на некотором участке тела 
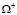свободную от воздействий границу 
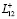(рис. 1). При tk ≤ t < tm эта граница подвергается нагреву и, наконец, при t = tm на участке 
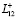тела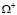 
происходит его сращивание с нагретым до некоторой температуры телом 
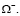При этом тело 
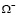сращивается по участку его границы 
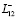(см. рисунок).
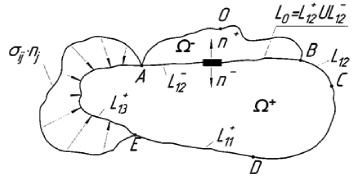
Расчетная схема: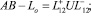 
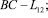
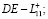
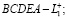
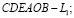
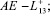
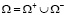
При t = tm происходит перемещение плазмотрона в соседнюю точку и процесс повторяется. Обозначим вектор перемещений, тензоры деформаций, напряжений и температурное поле соответственно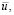 
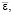
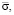
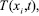их компоненты –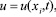 
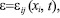
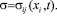
При t < tk состояние тела известно и определяется предыдущей историей обработки изделия, т.е.
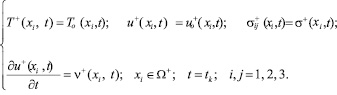(1)
При tk ≤ t < tm к участку границы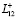 
тела W осуществляется подвод тепла, происходит его разогрев, возникает некоторая система температурных деформаций и напряжений. В этом случае придем к следующей системе уравнений и граничным условиям:
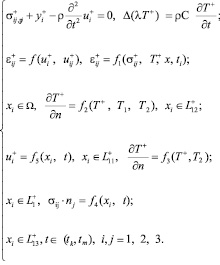(2)
где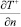 
– производная от температуры по нормали к границе 
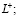T2 – то же на свободной от нности; 
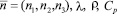– теплофизические параметры области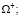 
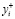– плотность объемной силы.
В качестве начальных условий (2) следует использовать соотношение (1). При t = tm производится сращивание основного изделия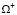 
и участка покрытия 
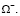При этом их границы 
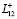и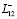 
трансформируются в общую границу Lo После сращивания теплообмен с окружающей средой происходит уже на границе L вновь образованного тела Ω
В этом случае состояние изделия описывается такой системой уравнений, граничными и начальными условиями:
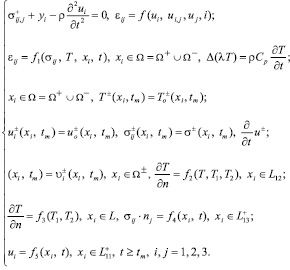(3)
При выполнении следующих условий на границе взаимодействия вновь напыленного участка покрытия с изделием:
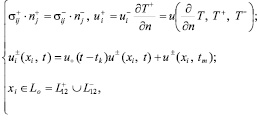(4)
где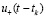 
– ассиметричная функция Хевиссайда; l, r, Cp – теплофизические параметры области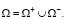 
Полученные соотношения могут быть использованы в численном моделировании для предварительного выбора диапазона технологических параметров режима напыления, при которых обеспечиваются условия формирования плазменных газотермических покрытий с экстремальным комплексом эксплуатационных свойств. При этом окончательный выбор режимов напыления обеспечивается экспериментальным исследованием свойств покрытий в выбранных диапазонах.
Заключение
Процесс формирования плазменных покрытий может быть формализован с использованием систем уравнений (1)…(4). При этом вопросы сходимости, существования, единственности и устойчивости могут быть решены на основе конкретных граничных условий и уравнений состояния. Проведенные исследования позволили установить новые закономерности, обеспечивающие условия для получения плазменных покрытий с заданным комплексом эксплуатационных свойств.
Библиографическая ссылка
Кравченко И.Н., Сельдяков В.В., Бобряшов Е.М., Пузряков А.Ф. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА РАЗВИТИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ ПРИ ФОРМИРОВАНИИ ПЛАЗМЕННЫХ ПОКРЫТИЙ // Современные наукоемкие технологии. – 2013. – № 11. – С. 77-80;URL: https://top-technologies.ru/ru/article/view?id=33525 (дата обращения: 21.11.2024).