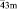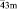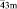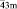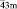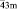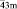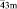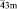Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Дерлугян П.Д. 1, 2 Иванов В.В. 1, 2 Иванова И.В. 1 Логинов В.Т. 1, 2 Торопков И.А. 2

---

1 ФГУП ОКТБ «ОРИОН»

2 Южно-Российский государственный технический университет

Проанализированы вероятные изосимметрийные и деформационные модификации некоторых наноструктур с атомными оболочками тетраэдрической ветви классификации фуллеренов и их возможное влияние на трибологические свойства покрытий.

Статья в формате PDF

395 KB

структурно-фазовая разупорядоченность

композиционные покрытия

наноалмаз

наноструктуры

атомные оболочки фуллеренов

1. Урусов В.С. Теоретическая кристаллохимия. – М.: Изд-во МГУ, 1987. – 275 с.

2. Иванов В.В. Комбинаторное моделирование вероятных структур неорганических веществ. – Ростов-на-Дону: Изд-во СКНЦ ВШ, 2003. – 204 с.

3. Ivanov V.V., Talanov V.M. // Crystallography Reports. – 2010. – Т. 55, № 3. – С. 362–376.

4. Ivanov V.V., Talanov V.M. //Russian Journal of Inorganic Chemistry. – 2010. – Т.55, № 6. – С. 915–924.

5. Ivanov V.V., Talanov V.M. // Glass Physics and Chemistry. – 2008. – Т. 34. № 4. – С. 401–435.

6. Bespalova Zh.I., Ivanov V.V., Smirnitskaya I.V., et al. // Russian Journal of Applied Chemistry. – 2010. – Т.83. – № 2. – С. 242–246.

7. Ivanov V.V., Bespalova Zh.I., Smirnitskaya I.V., et al. // Russian Journal of Applied Chemistry. – 2010. – Т. 83. – № 5. – С. 831–834.

8. Ivanov V.V., Talanov V.M., Shabel’skaya N.P. // Inorganic Materials. – 2001. – Т. 37. – № 8. – С. 839–845.

9. Ivanov V.V., Talanov V.M. // Physica Status. Solidi (A) Applied Research. – 1990. – T. 122. – № 2. – K109.

10. Иванов В.В., Таланов В.М. // Журнал структурной химии. – 1992. – Т. 33. – № 5. – С. 96–102.

11. Иванов В.В., Таланов В.М. // Неорганические материалы. – 1992. – Т.28. – № 8. – С. 1720–1725.

12. Иванов В.В., Таланов В.М. // Неорганические материалы. – 1995. – Т.31. – № 2. – С. 258–261.

13. Иванов В.В. // Изв. вузов. Сев.-Кавк. регион. Естеств. науки. – 1996. – №1. – С. 67–73.

14. Ivanov V.V., Talanov V.M., Shirokov V.B., Talanov M.V. // Inorganic Materials. – 2011. – Т.47. – № 9. – С. 990–998.

15. Таланов В.М., Широков В.Б., Иванов В.В., Таланов М.В. // Междунар. журн. эксп. образования. – 2011. – № 4. – С. 89–90.

16. Таланов В.М., Широков В.Б., Иванов В.В., Таланов М.В. // Междунар. журн. эксп. образования. – 2011. – № 4. – С. 90–92.

17. Talanov V.M., Shirokov V.B., Ivanov V.V., Talanov M.V. // Acta Crystallographica. A. – 2011. – Vol. 67. – P. 805.

18. Таланов В.М., Широков В.Б., Иванов В.В., Таланов М.В. // Кристаллография. – 2013. – Т. 58. – № 1. – С. 101–112.

19. Иванов В.В. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2001. – № 3. – С. 60–61.

20. Иванов В.В. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. Спецвыпуск. Проблемы трибоэлектрохимии. – 2005. – С. 124–126.

21. Balakai V.I., Ivanov V.V., Balakai I.V., Arzumanova A.V. // Russian Journal of Applied Chemistry. – 2009. – Т.82. – № 5. – С. 851–856.

22. Иванов В.В., Щербаков И.Н. Моделирование композиционных никель-фосфорных покрытий с антифрикционными свойствами. – Ростов н/Д: Изд-во журн. «Изв. вузов. Сев.-Кавк. регион», 2008. – 112 с.

23. Щербаков И.Н., Иванов В.В., Логинов В.Т. и др. Химическое наноконструирование композиционных материалов и покрытий с антифрикционными свойствами. – Ростов н/Д: Изд-во журн. «Изв. вузов. Сев.-Кавк. регион. Техн. науки», 2011. – 152 с.

24. Иванов В.В., Иванов А.В., Щербаков И.Н., Башкиров О.М. // Изв. вузов. Сев-Кавк. регион. Техн. науки. – 2005. – № 3. – С. 46–49.

25. Иванов В.В., Щербаков И.Н., Иванов А.В., Башкиров О.М. // Изв. вузов. Сев-Кавк. регион. Техн. науки. – 2005. – № 4. – С. 62–64.

26. Ivanov V.V., Balakai V.I., Ivanov A.V., Arzumanova A.V. // Russian Journal of Applied Chemistry. – 2006. – Т. 79. – № 4. – С. 610–613.

27. Ivanov V.V., Balakai V.I., Kurnakova N.Yu., Arzumanova A.V., Balakai I.V., // Russian Journal of Applied Chemistry. – 2008. – Т. 81. – № 12. – С. 2169–2171.

28. Щербаков И.Н., Иванов В.В. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2011. – № 5. – С. 47–50.

29. Кустов Е.Ф., Нефедов В.И., Карелина М.С. и др. // Журн. неорганической химии. – 2006. – Т.51, – № 11. – С. 1906–1915.

30. Talanov V.M., Fedorova N.V. // In: Handbook on Fullerene. Synthesis, Properties and Applications. – N-Y: Nova Science Publishers, Inc., 2012. – P. 151–195.

31. Иванов В.В., Таланов В.М. // Наносистемы: Физика, Химия, Математика. – 2010. – Т.1. – № 1. – С. 72–107.

32. Иванов В.В., Таланов В.М., Гусаров В.В. // Наносистемы: Физика, Химия, Математика. –2011. – Т.2. – № 3. – С. 121–134.

33. Иванов В.В., Таланов В.М., Гусаров В.В. // Наносистемы: Физика, Химия, Математика. – 2012. – Т.3. – № 4. – С. 82–100.

34. Патент № 2473711 РФ / Трофимов Г.Е., Щербаков И.Н., Шевченко М.Ю., Логинов В.Т., Дерлугян П.Д., Дерлугян Ф.П., Иванов В.В. – Опубл. 27.01.2013. – Бюл. № 3.

Тетраэдр Т и его усеченная форма – лавесовский тетраэдр L’T – обладают симметрией группы Td (`43m) и являются достаточно компактными полиэдрами. Как устойчивые структурные фрагменты они зарекомендовали себя, в частности, в тетраэдрических и октатетраэдрических структурах различных классов неорганических соединений (фазы Лавеса в интерметаллидах [1], многочисленные твердые растворы со структурой шпинели [2–13] и др.). Отметим, что наличие в структурах веществ фрагмента в виде лавесовского тетраэдра или комплекса из пяти соединенных вершинами тетраэдров могут обусловить чрезвычайно низкие величины межатомных расстояний типа Ме-Ме, необычные орбитальные или магнитные упорядоченные состояния и другие структурные особенности [14–18].

В соответствии с [19–23] трибологические свойства поверхности композиционных покрытий (КП) существенно зависят от эффекта синергизма, который определяется, в частности, наноструктурным параметром, характеризующим объемную долю наночастиц фаз твердых компонент трибосопряженных поверхностей. В зависимости от фазового состава КП величина этого параметра составляет 0,03–0,17 [24–28]. При использовании наноалмаза в качестве модификатора поверхности покрытия в процессе трения возможно образование различных фуллеренов, в том числе и с тетраэдрическими оболочками. Проанализируем их вероятные изосимметрийные и деформационные модификации.

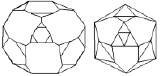
Топологические преобразования тетраэдра за счет сплиттинг-преобразования его вершин могут быть представлены следующим образом (рис. 1):

тетраэдр Т{333} → усеченный тетраэдр tT (L’T){366} → октаэдр O{3333} → дуальный тетраэдр Тd{333} → дуальный усеченный тетраэдр tTd(L’Td){366};

усеченный тетраэдр tT (L’T){366} → усеченный тетраэдр Лавеса tL’T (2{36.12} + {3.12.12}) → 20-гранник (2{336} + {3636}).

Характеристики всех полученных выше полиэдров с кубической симметрией тетраэдра или октаэдра, в том числе расчетные значения диаметра соответствующих им фуллеренов и возможные составы оболочек углеродсодержащих наноструктур в соответствии с [29], представлены в табл. 1.

          а                   б                    в                   г                    д                   е                   ж

Рис. 1. Проекции оболочек для тетраэдра Т{333} (а) и его топологических производных из основной ветви сплиттинг-преобразования вершин:tT (L’T){366} (б); O{3333} (в); tTd (L’Td){366} (г); Тd{333} (д) tL’T 2{36.12} + {3.12.12} (е); 20-гранник 2{336} + {3636} (ж)

Таблица 1

Характеристика полиэдров

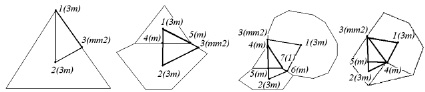
Аналогичные данные для указанных выше полиэдров с кубической симметрией могут быть получены при анализе фундаментальной области точечной группы Td. Симметрический комплекс группы содержит центр симметрии, 6 поворотных осей симметрии 2-го порядка, 4 поворотные оси симметрии 3-го порядка, 3 инверсионные оси симметрии 4-го порядка и 6 плоскостей симметрии m. Фундаментальная область группы – неправильная трехгранная пирамида, ребрами которой являются ближайшие друг к другу оси симметрии 2-го и 3-го порядка (рис. 2). В [30] методом анализа фундаментальных областей точечной группы перечислены группы симметрии всех возможных симметрийно неэквивалентных разновидностей молекул фуллеренов, которые могут возникнуть в результате ее непрерывных деформаций. В соответствии с этим методом для молекул фуллеренов С12, С18 и С36 выделены различные типы структурных элементов, которым соответствуют симметрийно неэквивалентные разновидности (табл. 2). В таблице используются обозначения структурных элементов, приведенные на рис. 2, б-г.

Таким образом вероятно, что при модифицировании КП наноалмазом фазовая и структурная разупорядоченность углеродсодержащих наночастиц на их поверхности после трибовоздействия может быть обусловлена наличием как слоистых фрагментов графитоподобных структур, так и фуллереноподобных наночастиц с симметрией группы Td и ее возможных деформационных модификаций. Все эти наночастицы могут рассматриваться как частицы твердой компоненты покрытия, проявляющие свойства твердых смазочных материалов. В частности, это косвенно подтверждается результатами трибологических испытаний соответствующих твердосмазочных антифрикционных покрытий, полученных с использованием наночастиц алмаза [34].

             а                        б                          в                           г

Рис. 2. Структурные элементы и их локальная симметрия в фундаментальной области точечной группы Td:а – Т{333}; б – tT (L’T){366}; в – (2{36.12} + {3.12.12}); г – 20-гранник (2{336} + {3636})

Таблица 2

Структурные состояния молекул фуллеренов С12, С18 и С36.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ, соглашение № 14.U01.21.1078.

Библиографическая ссылка