Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ильяшева Г.И. 1 Саябаева А.Р. 1

---

1 Кокшетауский государственный университет им. Ш. Уалиханова

Эта работа показывает соотношение между стационарной задачей Шредингера и нестационарной задачей для одномерного волнового уравнения с нелокальным потенциалом. Эта связь выражается в определении дискретного спектра стационарной задачи по данным нестационарной задачи.

Статья в формате PDF

603 KB

дискретный спектр

стационарная задача

нестационарная задача

1. Владимиров В.С. Уравнения математической физики. – М.: Наука, 1971. – 512 с.

2. Романов В.Г. Некоторые обратные задачи для уравнений гиперболического типа. – Новосибирск: Наука, 1972. – 301 с.

3. Фаддеев Л.Д. Обратная задача квантовой теории рассеяния II // Современные проблемы математики. – М.:ВИНИТИ, 1974. – С. 93–180.

4. Шадан К., Сабатье П. Обратные задачи в квантовой теории рассеяния. – М.: Мир, 1980. – 408 с.

Большой практический интерес представляет определение собственных значений сложных дифференциальных операторов.

Рассмотрим в пространстве функций одной переменной уравнение Шредингера [4]

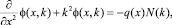(1)

где x, y ∈ R, k > 0 и

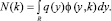
Пусть q – вещественная локально-интегрируемая функция, удовлетворяющая условиям:

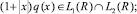(2)

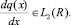(3)

Обозначим множество всех функций q, удовлетворяющих условиям (2) и (3) через М.

Среди множества решений уравнения (1) будут интересовать те решения, которые на бесконечности 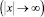удовлетворяют условиям излучения Зоммерфельда [1].

Рассмотрим оператор Шредингера

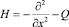
где Q – оператор, действующий по правилу

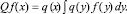
Основным результатом теории рассеяния [3] является утверждение о том, для оператора H существует инвариантное относительно H разложение пространства L2(R) в ортогональную сумму

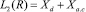
собственных подпространств, соответствующих дискретному и абсолютно-непрерывному спектру этого оператора.

Оператор Н имеет конечное число собственных значений, причем эти значения действительные положительные. Обозначим их через 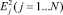, а соответствующие им собственные функции – через ψj, через qj– коэффициенты Фурье в разложении функции q по собственным функциям ψj

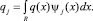
В данной работе предлагается метод определения собственных значений оператора Н из данных обратной нестационарной задачи. Дадим ее постановку.

Известно [2], что постановка обратной задачи неразрывно связана с постановкой прямой задачи, которая имеет следующий вид: в пространстве функций одной переменной для уравнения

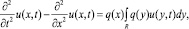(4)

в области 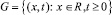найти функцию 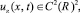удовлетворяющую уравнению (4) и начальным условиям

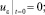(5)

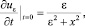(6)

где ε – некоторая константа, ε > 0.

Сразу оговорим, что функция q(x) должна удовлетворять условиям (2)и (3).

Введем обозначение

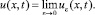(7)

Положим, что при t < 0 функция u(x, t) продолжается нулем.

Поставим для уравнения (4) следующую обратную задачу: найти функцию q(x) ∈ C(R), если задано дополнительное условие

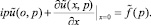
В процессе исследования прямой нестационарной задачи получено ее свойство, выраженное в следующей теореме.

Теорема 1. Для функции (7) имеет место соотношение

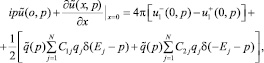(8)

где 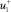, 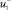– собственные функции непрерывного оператора Шредингера; C1j, C2j – некоторые коэффициенты.

Так как, согласно постановке обратной нестационарной задачи, функция

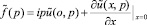
считается известной, то из соотношения (8) следует, что для функции 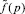имеет место также следующее представление

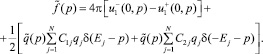(9)

Равенство (9) выражает связь данных обратной нестационарной и стационарной задач.

Имеет место

Утверждение. Для собственных значений 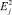оператора Шредингера справедливо равенство

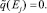
Тогда в силу утверждения 1 два члена во вторых квадратных скобках выражения (9) в обобщенном смысле равны нулю. Следовательно,

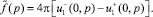
Доказана

Теорема 2. При p = Ej функция 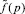равна нулю, т.е.

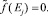
Библиографическая ссылка