Рассмотрим следующую краевую задачу:
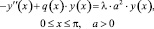 (1)
(1)
с граничными условиями
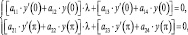 (2)
(2)
где λ – спектральный параметр,
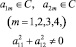
либо 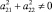 (λ входит в граничные условия),
(λ входит в граничные условия), 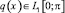 .
.
Теорема 1. Асимптотика собственных значений дифференциального оператора (1)–(2) в случае 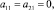
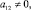
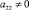 имеет следующий вид:
имеет следующий вид:
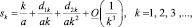 (3)
(3)
где
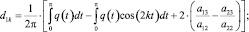 (4)
(4)
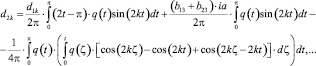 (5)
(5)
Теорема 2. Асимптотика собственных функций yk(x, s) дифференциального оператора (1)–(2), нормированных условием
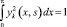
в случае 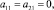
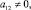
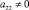 имеет вид:
имеет вид:
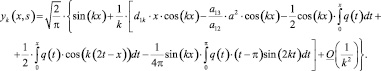 (6)
(6)
Теоремы 1 и 2 доказываются методами главы 5 монографии [1].
Библиографическая ссылка
Митрохин С.И. О краевой задаче со спектральным параметром в граничных условиях // Современные наукоемкие технологии. 2013. № 1. С. 99-99;URL: https://top-technologies.ru/ru/article/view?id=31244 (дата обращения: 13.03.2026).



