Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Аристархова А.В.

Статья в формате PDF

169 KB

Конформно полуплоские, то есть автодуаль­ные и антиавтодуальные, 4-мерные многообразия (например, [1]-[7]) играют достаточно значимую роль в современной науке в силу связи их геомет­рии с геометрией эйнштейновых многообразий [8] и с твисторной геометрией [9]. В настоящей работе построен 5-мерный контактный аналог автодуаль­ной геометрии. А именно, введено понятие кон­формно полуплоских (контактно-автодуальных или контактно-антиавтодуальных) 5-мерных почти кон­тактных метрических многообразий и рассмотрена контактно-автодуальная геометрия 5-мерных мно­гообразий Кенмоцу.

Рассмотрим модуль X(М) гладких векторных полей и алгебру С^∞(М) гладких функций на глад­ком 5-мерном многообразии М.

Напомним [10], что почти контактной мет­рической структурой (короче, АС- структурой) на М называется четверка (Ф,ξ,ц,д = {.,.}) тензор­ных полей на М, где Ф - эндоморфизм С^∞(М) - модуля X (М) , называемый структурным эндо­морфизмом, ξ и п - векторное и ковекторное по­ля, называемые характеристическим вектором и контактной формой соответственно, g - билинейная симметричная положительно определенная форма на X (М) , называемая римановой структурой. При этом

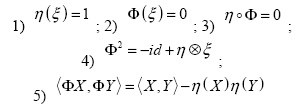
для любых X,Y e X(M).

Многообразие, на котором фиксирована АС - структура, называется почти контактным метриче­ским многообразием (короче, АС - многообразием).

В 1971 году Кенмоцу [11] ввел в рассмотрение новый класс АС -структур, характеризуемых для любых гладких векторных полей Х и Y тождеством

-риманова связность метрики

Такие АС - структуры называются структурами Кенмоцу. Многообразие, на котором фиксирована структура Кенмоцу, называется многообразием Кенмоцу.

Пусть 5-мерное ориентированное АС -многообразие. В этом случае классический тензор С Вейля можно рассматривать как эндоморфизм модуля Λ₂(М), который внутренним образом определяет эндо­морфизм С модуля Λ₂(L), задаваемый одной из трех эквивалентных формул:

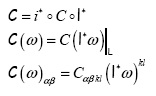
где j - вложение на L с X(M), I = -Ф² - естествен­ный проектор на 4-мерное контактное распределе­ние L, 2-форма I (ω)єЛ₂(М) - антиувлечение 2- формы ωєΛ₂) при отображении I, а C(I*ω)|_L - сужение 2-формы C(I* ω) єΛ₂(М) на L. Кроме то­го, Λ₂(Ц) = Λ+(Ц)©Λ^-(Ц), где Λ⁺(L) , Λ^-(Ц) - собственные подмодули эндоморфизма *;Λ₂(L)→Λ₂(L), соответствующие собственным значениям 1 и -1. Заметим, что индексы k, l пробегают значения 0,1,2,1^€,2^€, а индексы а, в - значения 1,2,1^€,2^€, где a^€ = a + 2.

Таким образом, 5-мерное AC -многообразие будем называть контактно - автодуальным (короче, С-автодуальным) многообразием, если С(ω) = 0 для любых 2-форм ω€Λ⁺(L). Аналогич­но, 5-мерное AC -многообразие будем называть контактно-антиавтодуальным (короче, С-антиавтодуальным) многообразием, если С(ω) = 0 для любых 2-форм ω <Λ⁺(L). При этом, 5-мерное AC - многообразие называется контактно конформно полуплоским (короче, С-конформно полуплоским), если оно является контактно-автодуальным или контактно-антиавтодуальным.

С учетом введенного определения был уста­новлен критерий контактной автодуальности 5- мерных многообразий Кенмоцу и доказано необходимое условие их контактной антиавтодуальности. А именно:

Теорема 1. 5-мерное многообразие Кенмоцу является контактно-автодуальным многообразием тогда и только тогда, когда

где

Теорема 2. Если 5-мерное многообразие Кенмоцу является контактно-антиавтодуальным мно­гообразием, то его скалярная кривизна к = -20.

В силу справедливости теоремы 1, была дока­зана следующая теорема:

Теорема 3. 5-мерное многообразие Кенмоцу контактно-автодуально тогда и только тогда, ко­гда оно является многообразием точечно постоян­ной Ф- голоморфной секционной кривизны с.

Учитывая указанные результаты и результаты [12], получаем:

Теорема 4. 5-мерное многообразие Кенмоцу М является контактно-автодуальным многообра­зием тогда и только тогда, когда оно канонически конциркулярно одному из следующих многообра­зий, снабженному канонической косимплектической структурой:

где С², СР², СН² - комплексное евклидово, ком­плексное проективное и комплексное гиперболи­ческое двумерные пространства, соответственно. В силу справедливости теоремы 2, была доказана следующая теорема:

Теорема 5. 5-мерное многообразие Кенмоцу контактно-антиавтодуально тогда и только тогда, когда оно является многообразием Эйнштейна с космологической константой ξ = -4.

Таким образом, полученные результаты вскрыли интересные связи между такими характе­ристиками многообразий Кенмоцу, как контактная автодуальность и постоянство голоморфной сек­ционной кривизны, как контактная антиавтодуальность и эйнштейновость, и др.

СПИСОК ЛИТЕРАТУРЫ:

1.     Atiyah M. F., Hitchin N. J., Singer I. M. Self- duality in four-dimensional Riemannian geometry. Proc. Roy. Soc. London. Ser. A. 1978. V. 362. P. 425-461.

2.     Chen B. Y. Some topological obstructions to Bochner-Kaehler metrics and their applications. J. Differential Geom. 1978. V. 13. P. 547-558.

3.     Bourguignon J.-P. Les varietes de dimension 4 a signature non nulle dont la courbure est har- monique sont d´Einstein. Invent. Math. 1981. V. 63. P. 263-286.

4.     Derdzinski A. Self-duality of Kahler mani­folds and Einstein manifolds of dimensional four. Compos. Math. 1983. V. 49. P. 405-433.

5.    Itoh M. Self-duality of Kahler surfaces. Compos. Math. 1984. V. 51. P. 265-273.

6.     Арсеньева О.Е. Автодуальная геометрия келеровых многообразий. Математический сбор­ник. 1993. Т. 184. №8. С. 137-148.

7.    Арсеньева О.Е., Кириченко В.Ф. Автоду­альная геометрия эрмитовых поверхностей. Мате­матический сборник. 1998. Т. 189. №1. С. 21-44.

8.   Бессе А. Многообразия Эйнштейна. Моск­ва. Мир. 1990. Т. 1, 2.

9.    Penrose R. The twistor programme. Math. Phis. Repts. 1977. V. 12. P. 65-76.

10.    Blair D.E. Riemannian geometry of contact and symplectic manifolds. Progr. in Math. 2003. Birk- hauser Boston, Basil, Berlin. 2003.

11.    Kenmotsu K. A class of almost contact Rie- mannian manifolds. Tohoku Math. J. 1972. V. 24. P. 93-103.

12.    Кириченко В.Ф. О геометрии многообра­зий Кенмоцу. Доклады Академии Наук. 2001. Т. 380. №5. С. 585-587.

Библиографическая ссылка