Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Глотов А.В. Гольтяпин В.В. Ложников Е.В.

Статья в формате PDF

372 KB

1. Введение

Развитие современной медицины обу­словлено появлением различных электронных приборов и устройств, которые позволяют по­лучать большой объем информации, количе­ственных и качественных показателей. В связи с этим появилось большое число методов, с помощью которых обрабатывается информа­тивный массив данных. Наибольший интерес представляют методы многомерного факторно­го анализа, являющиеся аналитическими мето­дами обработки биологических и медицинских результатов.

Использование в исследованиях понятия факторных нагрузок представляется актуаль­ным для анализа многочисленных параметров, характеризующих состояние больных с гене­тически детерминированными заболеваниями, обусловленными дисплазией соединительной ткани (ДСТ) [1].

Дисплазия соединительной ткани  группа генетически гетерогенных и клинически поли­морфных патологических состояний, объеди­ненных нарушением формирования соедини­тельной ткани в эмбриональном и постнатальном периодах [2].

Актуальность проведенной работы состоит в том, что проблемы диагностики дисплазии со­единительной ткани (ДСТ) обусловлены труд­ностями правильной оценки типичных наруше­ний метаболизма компонентов соединительной ткани, липидного обмена, иммунитета и эндотелиальной функции, сопутствующих этому син­дрому, а также необходимостью дифференциро­вать эти нарушения с использованием понятия факторной структуры.

Целью исследования является создание мо­дели группового факторного анализа, которая способна обнаружить основные скрытые зако­номерности, характеризующие состояния боль­ных дисплазией соединительной ткани, а также позволяющей выявить нарушение метаболизма и эндотелиальной дисфункции при дисплазии соединительной ткани.

Для реализации данной цели были постав­лены следующие задачи: формирование базы исходных показателей, характеризующих ДСТ, освоение математического аппарата, используе­мого для построения факторных моделей, разра­ботка алгоритма построения групповой фактор­ной модели, реализация полученного алгоритма в диагностике ДСТ, получение научно значимых результатов работы алгоритма и их адекватная интерпретация.

2. Материалы и методы

Для построения математической модели ис­пользованы биохимические, гематологические параметры, полученные при обследовании па­циентов с ДСТ. Проведено исследование гема­тологических показателей, характеризующих тромбоцитарноэндотелиальную дисфункцию (понтанная агрегация тромбоцитов (САТ), инду­цированная аденозиндифосфата и коллаген на агрегометре «Биола0 231LA» по методу J. Born в модификации З.А. Габбасова).

Непрямой иммунофлюоресцентный ана­лиз использовался для определения адгезивных макромолекул  рецептора CD44 лимфоцитов. Свободный оксипролин определялся по мето­дике R.E. Neuman и M.A. Logan в модификации П.Н. Шараева (2003 г.) [3]. Уровень фибронектина определялся в плазме с помощью стандарт­ной иммуноферментной тестсистемы (ЦНИВС им. И. И. Мечникова, Россия), проколлаген III типа  с помощью иммуноферментной тестсистемы «Labsystems» (Финляндия), холестерин липопротеидов различной плотности и триглицериды  иммуноферметным методом с помо­щью стандартных тестсистем.

3. Теоретические основы построения групповой факторной модели и алгоритм реализации

Основная цель факторного анализа состоит в выявлении гипотетических величин, или фак­торов, по большому числу экспериментальных данных, а задачей факторного анализа является нахождение простой структуры, которая бы до­статочно точно отражала и воспроизводила ре­альные, существующие в природе зависимости.

Пусть данные распределены по нормаль­ному закону распределения и записаны в виде матрицы X = (x_ij, где индекс i = 1, 2, m отно­сится к переменным, а j = 1, 2, ... , n к индивиду­умам. Для приведения такого типа переменных к одному масштабу применяют классическую стандартизацию. Матрицу стандартизованных данных будем обозначать за Z = (z_ij, тогда все средние значения переменных Z равны нулю, а дует, что для корреляционной и ковариационной все дисперсии равны единице [4]. Из этого следует, что для корреляционной и ковариационной матриц R и S имеет место соотношение:

 

Групповой метод отличается от всех других методов выделения факторов тем, что одновре­менно на одном шаге получают сразу несколько факторов. Основная отличительная особенность метода состоит в том, что вначале определяются группы переменных, которые тесно коррелиру­ют между собой, и затем выделяется ряд фак­торов, из которых каждый соответствует такой группе. В данном методе каждый раз перед вы­делением факторов необходима априорная груп­пировка переменных. Кроме этого, необходимо оценить диагональные элементы корреляцион­ной матрицы  общности, которые представ­ляют собой части единичных дисперсий пере­менных, которые обозначим за вектор столбец размерностью m. Один из самых распространенных методов оценки общностей является усреднение коэффициентов корреля­ции данного параметра:

При необходимости, можно получить точ­ные общности, используя метод минимальных остатков [5].

Для получения корреляционной групповой матрицы нужно сгруппировать элементы матри­цы с общностями на главной диагонали. Груп­пировку проводим априорно, группируем m па­раметров по r группам G_p (p = 1,...r).

Для вычисления дисперсии факторов и ко­эффициента ковариации между ними удобно посчитать сначала некоторые суммы коэффици­ентов корреляции:

где p и q - номера соответствующих выделенных групп.

С помощью этих сумм легко получить корреляционную групповую матрицу Ф = (ф). Для этого воспользуемся формулой:

Далее выразим через суммы исходных ко­эффициентов корреляции значения коэффици­ентов корреляции между параметрами и факто­рами, то есть элементы косоугольной факторной структуры. Эти элементы будут выражаться сле­дующим образом:

В итоге получаем матрицу V = (v_pp) косоу­гольной факторной структуры, которая имеет размерность mxr [6].

4. Алгоритм построения групповой факторной модели

1.    Стандартизация  входных  параметров

2.  Нахождение корреляционной матрицы по формуле (1) и оценка общностей по формуле (2).

3.  Вычисление суммы коэффициентов кор­реляции каждого параметра со всеми параме­трами каждой из групп по формуле (3) и расчет матрицы суммы коэффициентов корреляции между всеми параметрами группы G_p и всеми параметрами группы G_q по формуле (4).

4.  Получение групповой корреляционной матрицы , используя формулу (5).

5.  Расчет матрицы V = (v._p) косоугольной факторной структуры, используя (6).

6. Результаты и выводы

В результате исследовательской работы по­лучена следующая факторная структура, пред­ставленная на таблице.

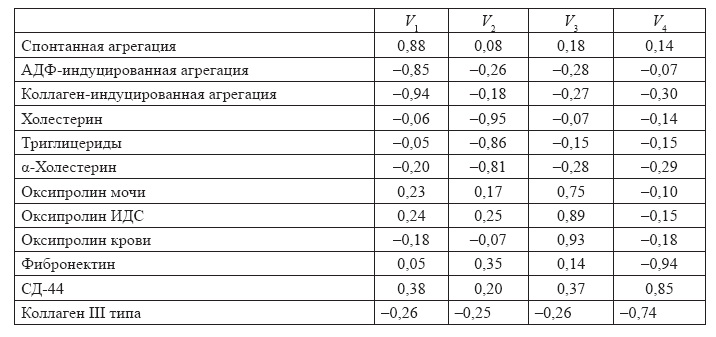
Анализ полученной факторной структуры позволяет сделать вывод:

Первая группа параметров относится к агре­гациям. Коллагениндуцированная агрегация обусловлена повреждением сосудистой стенки, АДФиндуцированная агрегация показывает по­явление факторов в сосудистом русле, спонтан­ная агрегация  это самоиндуцированная агрега­ция тромбоцитов.

Вторая группа параметров (холестерин, триглицериды, аХолестерин) относится к фак­тору нарушения липидного обмена, то есть на­копления липидов в плазме и снижение их со­единений в мембране клетки. Таким образом, мембрана тромбоцитов теряет способность к текучести, становится ломкой. Тромбоцитарные дисфункции связаны с нарушением адгезии к коллагену, транспорта внутриклеточного каль­ция и реакции высвобождения.

Третья группа параметров отвечает за фак­тор разрушения стенки сосуда, поскольку избы­ток оксипролина, входящего в состав коллагена, указывает на то, что средняя стенка сосуда де­фективная.

Четвертая группа параметров образует фак­тор, который характеризует степень разрушения волокон соединительной ткани. Фибронектин указывает на степень склеивания клеток. Клю­чевым в миграции клеточных элементов крови при ДСТ являются СД44  глюкоронат хряща. Процессы миграции клеточных элементов при ДСТ нарушены, что существенно влияет на со­стояние адаптивного иммунитета. Коллаген по­казывает на фактор поражения стенки сосудов. Чем выше содержание коллагена, тем больше поражения сосудистой стенки.

Полученная матрица косоугольной фактор­ной структуры позволяет выявить существен­ные взаимосвязи между биохимическими и ге­матологическими параметрами у больных ДСТ. Разработанная методика может применяться в диагностике и выявлении гематологических, биохимических и иммунологических отклоне­ний у пациентов с ДСТ.

СПИСОК ЛИТЕРАТУРЫ

1.  Яковлев В.М., Нечаева Г.И., Глотов А.В. Терминология, определение с позиции, клас­сификация врожденной дисплазии соедини­тельной ткани // Врожденная дисплазия со­единительной ткани: тезисы регионального симпозиума.  Омск, 1990.  С. 35.

2.  Яковлев В.М., Глотов А.В., Ягода А.В. Иммунопатологические синдромы при наслед­ственной дисплазии соединительной ткани. Ставрополь, 2005.

3.  Шараев П.Н., Иванов В.Г., Гаврилов А.Л. Методы лабораторного исследования показате­лей обмена коллагена в биологических жидко­стях: Информационное письмо для врачей кли­нической лабораторной диагностики.  Ижевск, 2003.  С. 19.

4.  Иберла К. Факторный анализ.  М.: Ста­тистика, 1980.

5.  Гольтяпин В. В. Вычислительные аспек­ты метода минимальных остатков при разре­шении варианта Хейвуда. // Сибирский журнал индустриальной математики.  2005.  Том VIII, №3(23).  С. 145151.

6.  Харман Г. Современный факторный ана­лиз.  М.: Статистика, 1972.

Библиографическая ссылка