Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Ермолаева Л.В.

Статья в формате PDF

124 KB

Система GERT-моделей позволяет включать случайные отклонения и неопределенность, возникающие непосредственно во время выполнения каждой отдельной задачи алгоритма. Следовательно, в полученный результат уже включены все случайные колебания и нет необходимости  вносить в него дополнительные поправки, не считая тех, которые соответствуют аварийным  ситуациям при завершении процессов. В сущности, эти поправки характеризуют реальную ситуацию в рамках существующей технологии управления процессами.

Рассмотрим подход к минимизации затрат и времени при формировании распределенных процессов с учетом стохастической реализации процесса. В качестве базовой модели рассмотрим простую ациклическую детерминированную модель, которая имеет "GERT-подобную узловую логику" [1]. Такую модель будем называть сетью для формирования, подчеркивая этим термином, что план реализации производственного процесса выбирается в процессе формирования, т.е. принимается решение о том, какие операции процесса должны быть выполнены для минимизации некоторой целевой функции.

Пусть N - ациклическая сетевая модель распределенного процесса с источниками и стоками, где множество узлов обозначается V, а множество дуг -  E. Предположим, что N имеет только один исток, который обозначается через r и соответствует началу формируемого процесса. Предполагается также, что один из стоков  N представляет собой успешное завершение всех операций процесса и обозначается s. Оставшиеся стоки, если они есть, могут представлять собой различные виды неудачного завершения или прерывания процесса.

Ациклическую сетевую модель N(V,E) только с одним истоком и со стоками назовем сетью для формирования распределенного процесса, если каждый узел i из N определен через  входную характеристику   и  выходную характеристику , где множество узлов обозначается V, а множество дуг - E;  - мощность множества предшественников и последователей узлов I соответственно.  

Характеристики, формирующие GERT-подобную узловую логику, имеют следующие значения.

(а) Узел активируется сразу же, как только входные действия  завершаются.

(б) Как только узел i активирован, то не более  выходных действий начинает выполняться. Если узел i не активируется, то ни одно выходное действие не выполняется.

Для источника r полагаем , т.е. он всегда активирован. Кроме того,  для , где S -  множество стоков  N.

Нужно отметить, что, во-первых, если =1, тогда узел i имеет OR-вход, и, если , то тогда i имеет AND-вход. И если "не более" заменяется на "точно" в (б), то =1 соответствует вероятностному выходу, а  соответствует детерминированному выходу. Во-вторых, если данная сеть N для формирования процессов имеет множество источников R (|R|>1) и множество R´ ⊂ R, R´  ≠0 активизируется в начале выполнения набора операций, то можно формально перевести N в соответствующую одно-истоковую сеть следующим образом.

Введем новый единый источник r₀ и для каждого  введем вспомогательную дугу ry < r₀, i >0.

Кроме того, установим  и определим

Для формализации условий узловой логики введем дуговые переменные (<i,j> ):

и узловые переменные

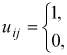
где  u_r =1, т.е. источник всегда активируется.

Тогда условия узловой логики (а) и (б) могут быть переписаны в следующем виде:

            (2.2.1)

  где                    (2.2.2)

                                       (2.2.3)

Если u_i =1 в (2.2.1), то это значит, что в результате активации узла i выполняется, по крайней мере,  входящих воздействий. Если u_i =0 в (2.2.2), то это значит, что узел i не активирован, т.к. менее чем  входящих действий выполнено. Таким образом, оба эти неравенства вместе соответствуют (а). Полагая  u_i =1 и u_i =0 в (2.2.3), обеспечиваем выполнение (б).

Так как сетевая модель для формирования распределенных процессов ациклична, то каждая операция соответствующего процесса либо выполняется только один раз, либо не выполняется вообще.

СПИСОК ЛИТЕРАТУРЫ:

1. Pritsker A.A. GERT: Graphical Evaluation and Review Technique. Part.1, Fundamentals. The Journal of Industrial Engineering (May 1966), pp. 67-101.

Библиографическая ссылка