Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Саитова Я.А.

Статья в формате PDF

263 KB

M_k = M.                               (1)

Толщина стенки  мала по сравнению с размерами поперечного сечения цилиндра. Вследствие малости h можно полагать, что касательные напряжения  постоянны по радиусу. Уравнение равновесия в этом случае можно проинтегрировать. В результате получим

• 2 πR²h = M,                                 (2)

где R =  - радиус срединной поверхности рассматриваемой цилиндрической оболочки.

Принимаем гипотезу плоских сечений, в соответствии с которой поперечные сечения, как в пределах упругости, так и за пределами упругости остаются плоскими, а радиусы прямолинейными.

В поперечных сечениях бруса возникают касательные напряжения =(r) . Парные им напряжения возникают в продольных сечениях бруса. В упругой стадии работы бруса напряжения  распределяются вдоль радиуса по линейному закону, [1]. За пределами упругости линейный закон нарушается.

Уравнение равновесия отсеченной части бруса

• 2 πR²h  = M                 (3)

При построении математической модели кинетики процесса упругопластического деформирования материалов на основе теории неизотермического течения вводим параметр τau , определяющий развитие процесса нагружения изделия (обобщенное время). Полагаем, что программа нагружения, определяемая функциями M = M(τau ), T = T (τau), задана. Определены также физико-механические характеристики конструкционного материала, которые меняются во времени в зависимости от параметров нагружения.

Программу нагружения разбиваем на ряд малых этапов, расчет которых выполняем последовательно. Каждой узловой точке ставим в соответствие параметр plast (признак пластичности), который принимает значение 0, если в рассматриваемой точке материал деформируется упруго, или 1, если имеет место пластическое течение.

Вводим в рассмотрение вектор состояния

{Z} = ,

который полностью характеризует напряженно-деформированное состояние исследуемой конструкции. Начальный вектор состояния {Z₀} полагаем заданным.

Алгоритм расчета конструкции шаговым методом включает две основных процедуры.

Первая процедура связана с определением приращений напряжений на шаге нагружения.Приращения термомеханической нагрузки на шаге составляют ΔM и ΔT.

Первая группа уравнений, определяющая статическую сторону задачи, определяется уравнением (3). Геометрическую сторону задачи определяет уравнение . (5)

Связь между напряжениями и деформациями в упругой стадии определяется законом Гука для сдвига:

.               (6)

Уравнения (3), (5), (6) полностью решают задачу.

Решим задачу в главных напряжениях, т.е.:

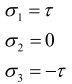
Далее последовательно вычисляем: ε₁, ε_2, ε₃ завершая тем самым решение задачи.

Вторая процедура связана с анализом параметров состояния в узловых точках конструкции в конце n-ro этапа нагружения. В упругих точках (plast = 0) проверяем условие пластичности

,

где δ - заданная величина допустимой погрешности.

Если условие   выполняется, точка остается упругой. Для точек, где выполняется условие H_e - δ < A_i < H_e + δ, полагаем plast = 1 и повторно решаем краевую задачу с учетом внесенных изменений.

Если в некоторых точках A_i > H_e + δ, это свидетельствует о несогласованности заданной величины этапа нагружения и величины допустимой погрешности. В этом случае необходимо изменить соответствующим образом их значения и повторно решить задачу.

СПИСОК ЛИТЕРАТУРЫ:

1. Феодосьев В.И. Сопротивление материалов. - М., Наука, 1970, 544 с, ил.
2. Термопрочность деталей машин. Под ред. И.А.Биргера и Б.Ф.Шорра. М., "Машиностроение". 1975. 455 с., ил.

Библиографическая ссылка