Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Потетюнко Э.Н.

Статья в формате PDF

360 KB

1.  Постановка задачи. Рассмотрим плоское стационарное турбулентное движение тяжёлой [1] вязкой жидкости по наклонной плоскости под действием силы тяжести (1).

Здесь ,  - проекции средней скорости частиц жидкости на оси Ox, Oz ; , = ,  - составляющие тензора напряжений в осредненном движении жидкости (2).

, , ,

, .   (1)

, , ,                                     (2)

где p¯ - осредненное гидродинамическое давление.

Функции R_xx, R_xz, R_zz  - добавочные напряжения Рейнольдса, представляющие суммарный эффект всех беспорядочных отклонений скоростей u´_x, u ´_z  от их средних значений u¯_x, u¯_z : , .

Функции ,   - сглаженные нелинейные слагаемые, порожденные отклонениями скоростей u´_x, u´_z  от их средних значений u¯_x, u¯_z . Постоянная ρ - плотность жидкости, g - ускорение свободного падения, μ - коэффициент внутреннего трения (коэффициент вязкости), μ =pv, v  - кинематический коэффициент вязкости. Начало координат взято на неподвижной наклонной плоскости Oxy. Ось Oy - горизонтальна, ось Oz направлена перпендикулярно к плоскости вверх, ось  лежит в наклонной плоскости и направлена вниз по направлению потока. Из всех массовых сил действует только сила тяжести (жидкость тяжёлая [1]): F_x =0 ,F_z = -g.

Считаем, что турбулентное движение жидкости в среднем происходит в направлении оси Ox и, что средняя скорость этого плоского движения существенным образом зависит лишь от координаты z: , , . В этом случае наиболее существенным из добавочных напряжений является лишь  [2]. То есть, полагаем R_xx = 0, Rz_z = 0 . Во многих источниках указывается, что турбулентное трение намного больше внутреннего трения. Поэтому во всём потоке , кроме тонкого вязкого подслоя , вблизи дна, полагаем , , , то есть, фактически в области  рассматриваем турбулентное движение идеальной жидкости без учета внутреннего трения, кроме тонкого вязкого подслоя вблизи дна, в котором рассматривается ламинарное движение вязкой жидкости [2].

Уравнение неразрывности для средних скоростей u¯_x, u¯_z  и их пульсаций u´_x, u´_z  имеют вид:

,  . (3)

Из первого уравнения (3) при u¯_z = 0 выводим, что . С учетом всех допущений, предположений и выводов из (1) следует:  

,  .  (4)

Эти уравнения выполняется в области , где h - толщина потока, δ  -  толщина ламинарного подслоя. Согласно [2] имеем:

,  . (5)

Постоянная k определяется из эмпирических данных [2].

Считаем, что сверху при z=h (h - толщина потока) поток ограничен свободной поверхностью, на которой выполняется динамическое условие равенства нормального напряжения в жидкости атмосферному давлению p₀=const. Условие равенства нулю касательного напряжения на свободной поверхности выполняется тождественно, так как турбулентный поток рассматривается без учёта внутреннего трения (μ =0 ). Кинематическое условие на свободной поверхности выполняется автоматически, так как мы полагаем . Зададим значение скорости u¯_x на свободной поверхности:  

На границе раздела вязкого подслоя и турбулентного потока ставятся условия равенства скоростей и напряжений. На неподвижной наклонной плоскости ставится условие равенства нулю скорости (условие прилипания). Итак, к системе (4), (5) формулируем следующие граничные условия:

, , ,
,  ; , .                                (6)

Здесь  - скорость стекания вязкой жидкости в ламинарном подслое,  - добавочное напряжение на границе ламинарного пограничного слоя (вязкого подслоя), δ - толщина ламинарного подслоя.

Введём ещё в рассмотрение расход жидкости Q через поперечное сечение потока:

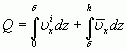 (7)

2.  Решение задачи (4)-(6). Из второго уравнения в (4) с учетом первого условия в (6) находим.

 (8)

Подставляя (8) в первое уравнение в (4), выводим:

,  , .  (9)

Из (5), (9) находим:

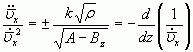   (10)

Считая кривизну функции  положительной, в (10) выбираем знак плюс.

Интегрируя (10) в пределах от δ до z, получаем представление для :

, .  (11)

Интегральное соотношение Кармана [2] приводит к равенству:

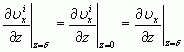.  (12)

То есть, на границе ламинарного подслоя «сшиваются» не только скорости, но и их первые производные. Для ламинарного вязкого подслоя имеем [2]:

,  , ,  .  (13)

Теперь из (11) и (13) выводим:

,

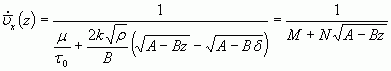.   (14)

Интегрируя (14), находим u¯_x:

, .  (15)

Два уравнения в (15) связывают две величины τ₀ и δ.

В настоящее время существуют приборы, позволяющие определять касательные напряжения на поверхностях, по которым движется вязкая жидкость [3, 4]. Поэтому в уравнениях (15) касательное напряжение на дне τ₀ можно считать известным. Полагая в (15) z=δ и используя (13), выводим уравнение:

  . (16)

Из уравнения (16) определяется δ по итерационному процессу, который сходится при значениях  много меньших единицы:

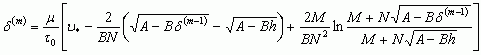, .  (17)

Теперь можно вычислить расход Q по формуле (7).Формулы (7), (8), (13), (15) и (17) дают решение задачи о турбулентном движении вязкой жидкости по наклонной плоскости с учётом вязкого подслоя.

Если касательное напряжение  на дне неизвестно, но известен расход Q, то равенство (7), с учётом формул (13), (15) и (17) представляет собой уравнение для τ₀, которое должно быть решено численно.

Список литературы

1. Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика, ч. I, М., физматгиз 1963 г., 584 с.
2. Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика, ч. II, М., физматгиз 1963 г., 728 с.
3. Рябинин А.Н. Моделирование пограничного слоя вблизи морского дна с переносимыми твёрдыми частицами. // Труды X Всероссийской конференции «Прикладные технологии гидроакустики и гидрофизики».- СПб.: Наука, 2010, С. 264-266.
4. Компаниец Л.А., Якубайлик Т.В., Питальская О.С. Опыт использования современных измерительных приборов для определения гидродинамических режимов водоёма. // Труды X Всероссийской конференции «Прикладные технологии гидроакустики и гидрофизики».- СПб.: Наука, 2010, С. 310-312.

Библиографическая ссылка