Игра двух лиц в условиях неопределённости задаётся набором
![]() .
.
Здесь ![]() - номера игроков,
- номера игроков, ![]() (
(![]() ) - множество ситуаций
) - множество ситуаций ![]() игры, каждая из которых образуется соответствующими стратегиями игроков:
игры, каждая из которых образуется соответствующими стратегиями игроков: ![]() - стратегия игрока верхнего уровня (1-й игрок, Центр),
- стратегия игрока верхнего уровня (1-й игрок, Центр), 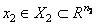 - стратегия игрока нижнего уровня (2-й игрок), Xi - подмножество в
- стратегия игрока нижнего уровня (2-й игрок), Xi - подмножество в 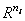 ,
, ![]() - множество неопределённостей,
- множество неопределённостей, ![]() - неопределённость, функция выигрыша i-го игрока задана непрерывной на
- неопределённость, функция выигрыша i-го игрока задана непрерывной на ![]() скалярной функцией
скалярной функцией ![]() , вектор
, вектор 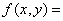
![]() .
.
Цель i-го игрока - выбор такой стратегии, чтобы в ситуации ![]() его выигрыш
его выигрыш ![]() принял возможно большее значение. При этом каждый игрок при выборе своей стратегии ориентируется на возможность реализации наименее благоприятных для него значений неопределённости
принял возможно большее значение. При этом каждый игрок при выборе своей стратегии ориентируется на возможность реализации наименее благоприятных для него значений неопределённости ![]() .
.
На множестве ![]() определим функции риска игроков
определим функции риска игроков
![]() .
.
Определение. Тройку 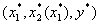
![]() назовём гарантированным равновесием с риском в исходной игре, если ситуация
назовём гарантированным равновесием с риском в исходной игре, если ситуация ![]() максимальна по Парето, т.е. для любых
максимальна по Парето, т.е. для любых ![]() несовместна система неравенств
несовместна система неравенств ![]() , причём по крайней мере одно из них строгое, а неопределённость y* максимальна по Парето в многокритериальной задаче
, причём по крайней мере одно из них строгое, а неопределённость y* максимальна по Парето в многокритериальной задаче ![]() , то есть для всех
, то есть для всех ![]() несовместна система неравенств
несовместна система неравенств
![]() ,
,
из которых хотя бы одно строгое.
Установлены неулучшаемость и внутренняя устойчивость гарантированного равновесия, его связь с седловой точкой, свойства функции риска.
Библиографическая ссылка
Родюков А.В. ПАРЕТОВСКОЕ РАВНОВЕСИЕ В ИЕРАРХИЧЕСКОЙ ИГРЕ С ФУНКЦИЯМИ РИСКА ИГРОКОВ // Современные наукоемкие технологии. 2007. № 5. С. 88-89;URL: https://top-technologies.ru/ru/article/view?id=24951 (дата обращения: 05.03.2026).



