Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы

Родюков А.В. Тараканов А.Ф.

В работе исследована двухуровневая иерархическая игра в условиях неопределённости с функциями риска при ограниченных стратегиях игроков. Между игроками уровней строится равновесие Нэша, а с помощью функций риска игроков воздействие неопределённости учитывается по Слейтеру. Показано, что предлагаемое гарантированное равновесие Нэша-Слейтера такой игре частично взаимозаменяемо и неулучшаемо. Выявлены свойства равновесия и функции риска. Сформулирован алгоритм решения.

Статья в формате PDF

132 KB

Игра двух лиц в условиях неопределённости задаётся набором

.           (1)

Здесь множество  - номера игроков,  ( ) - множество ситуаций  игры, каждая из которых образуется соответствующими стратегиями игроков: - стратегия игрока верхнего уровня (1-й игрок),  - стратегия игрока нижнего уровня (2-й игрок),  - неопределённость, функция выигрыша i-го игрока задана непрерывной на  скалярной функцией , вектор .

Цель i-го игрока - выбор такой стратегии, чтобы в ситуации  его выигрыш  принял возможно большее значение. При этом каждый игрок при выборе своей стратегии ориентируется на возможность реализации наименее благоприятных для него значений неопределённости . Предполагается, что игроки обладают достоверной информацией о стратегиях и множестве неопределённостей, игрокам известны функции выигрыша друг друга.

Игра протекает следующим образом. Первый игрок формирует подмножество стратегий

и информирует о нем игрока нижнего уровня (2-го). В ответ 2-й игрок формирует подмножество стратегий

,

выбирает стратегию  и информирует о ней 1-го игрока. Стратегия 2-го игрока явно зависит от стратегии Центра, который принимает окончательное решение. Затем вычисляются значения функций выигрыша игроков.

На множестве   определим функции риска игроков

, .

2. Определение равновесия и его свойства

Определение 1. Тройку  назовём гарантированным равновесием Нэша-Слейтера в игре (1), если существует такая неопределённость y*, что выполняются следующие условия:

1) ситуация  является равновесной по Нэшу, то есть

,              (2)

,            (3)

2) неопределённость y* максимальна по Слейтеру, то есть для всех  несовместна система неравенств

.          (4)

Множество гарантирующих равновесий 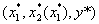 игры (1) обозначим N_s. Решением игры назовём совокупность 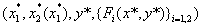, i =1,2.

Определение 2. Ситуации равновесия из множества N_s в игре (1) назовём частично взаимозаменяемыми, если для любых  и  выполняются равенства

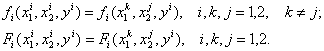                           (5)

Свойство 1. Ситуации равновесия из множества N_s в игре (1) частично взаимозаменяемы.

Доказательство. Возьмём произвольные  и . Согласно (2) и (3), имеем , i = 1,2, и поэтому

, , .                              (6)

Отсюда . Полагая здесь , , получим справедливость первого равенства в (5) при i = 1:

, .

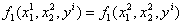Аналогично равенство доказывается для f₂.

Далее, подставляя в функцию  значения  и , получим

а с учётом (6) будет . Это равенство выполняется для любых i = 1,2 и . Поэтому при , k = 1,2, получим справедливость второго равенства в (5) при i = 1. Доказывается для F₂ аналогично. Свойство 1 доказано.

Таким образом, в отличие от обычных игр с равновесием Нэша (в которых взаимозаменяемости стратегий нет), в иерархической игре выполняется свойство частичной взаимозаменяемости ситуаций равновесия. Отметим, что для функции риска второе равенство в (5) означает полную взаимозаменяемость ситуаций равновесия.

Определение 3. Тройку  назовём неулучшаемым гарантирующим равновесием Нэша-Слейтера в игре (1), если для любых  выполняются неравенства

.

Свойство 2. Пусть  при любых ,  при любых . Тогда любая тройка  в игре (1) является неулучшаемым гарантирующим равновесием Нэша-Слейтера.

Доказательство. Пусть . Из определения множества 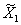 при  и из (2) соответственно следует, что

, , .

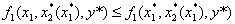Так как при любых  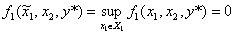 , то, полагая во втором неравенстве , получим

,

то есть  - неулучшаемое гарантирующее равновесие Нэша-Слейтера. Для функции f₂ доказательство аналогично. Свойство 2 доказано.

Рассмотрим иерархическую игру (1) как игру 1-го игрока со стратегией  и 2-го игрока (неопределённости) со стратегией , то есть

,                       (7)

где . Первый игрок стремится за счёт выбора  минимизировать , а 2-ой за счёт выбора  - максимизировать её.

Свойство 3. Решение Нэша-Слейтера (x*,y*) игры (1) является седловой точкой игры (7), то есть  для любых , .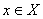

Доказательство. Так как y* максимально по Слейтеру, то несовместна система неравенств . Суммируя, получаем невозможность неравенства

.

Значит, . Далее, так как  - ситуация равновесия по Нэшу, то

,

.

Отсюда

,

.

В то же время

,

.

Очевидно, что  или , что и требуется. Свойство 3 доказано.

Пусть y^S- минимальная по Слейтеру неопределённость в задаче ,  - тройка из определения 1.

Свойство 4. Пусть , , . Тогда риск игрока в ситуации x* оценивается снизу неравенством .

Доказательство. Так как y* - максимальная по Слейтеру неопределённость, то для любых  найдётся индекс  такой, что

 или

.

Для всех  справедливо , поэтому при  будет . В силу , , получим 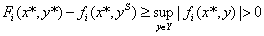. Свойство 4 доказано.

Содержательный смысл свойства 4 в том, что для получения большего гарантированного выигрыша при использовании функции риска, чем при использовании простых функций выигрыша , требуется больший риск.

Свойство 5. Пусть функции 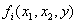, , удовлетворяют условию Липшица по совокупности переменных  с константами L_i. Риск игрока в ситуации x* оценивается сверху неравенством ( )

.

Доказательство. Как и при доказательстве свойства 4, имеем

  или

,

,

.

При y = y* получаем 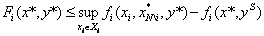. С использованием условия Липшица приходим к требуемой оценке. Свойство 5 доказано.

Полученная оценка говорит о том, что величина риска игрока зависит в целом только от его стратегии и размеров множества неопределённостей. Воздействие других игроков косвенно учитывается в константе Липшица. Если игроки не отступают от своих оптимальных стратегий , то оценкой риска сверху является .

Свойства 1-5 в достаточной степени раскрывают свойства предлагаемого равновесия и содержательный смысл функции риска игрока и дополняют тем самым результаты [1].

3. Алгоритм решения игры

1. Найти , удовлетворяющие равенствам

, .

2. Подставить  в функции  и получить функции  и . Эти функции выпуклы по обоим аргументам.

3. Вычислить величины

, ,

где  - граница множества M (вообще говоря, после 3 шага вместо 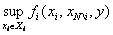 вычислены значения , i = 1,2, которые означают выигрыши игроков при наилучших для них действиях партнеров по иерархии и наилучшей неопределённости; однако легко показать, что стратегии и выигрыши игроков в этом случае не изменяются).

4. Составить функции риска игроков

,

и функцию .

5. Найти гарантированную неопределенность y* как решение задачи  и найти стратегии игроков , .

6. Вычислить риски игроков , i = 1,2.

Работа выполнена при финансовой поддержке Федерального агентства по образованию РФ.

СПИСОК ЛИТЕРАТУРЫ:

1. Жуковский В.И., Жуковская Л.В. Риск в многокритериальных и конфликтных системах при неопределенности. - М.: Едиториал УРСС, 2004.

Библиографическая ссылка