Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Резеньков Д.Н.

Статья в формате PDF

125 KB

В настоящее время известны два основных способа перевода непозиционного кода классов вычетов в позиционную систему счисления (ПСС) [1,2,3,6].

Задачей этих методов является восстановление заданного полинома А(z)∈GF(p^v) по совокупности его остатков ( а₁(z), а₂(z),..., а_n(z)).

Один из методов основывается на китайской теореме об остатках (КТО). Применение КТО обеспечивает однозначное отображение одномерных величин в многомерные и позволяет осуществлять восстановление полученного результата из непозиционной системы  счисления к двоичному позиционному виду[1,4,5,8].

Задача перевода n-мерного представления полинома A(z)∈GF(p^ν) представляется следующим образом: для заданного набора модулей р_i(Z),  i=1,2...,n, необходимо осуществить преобразование n-мерного образа A(z)=(a₁(z),a₂(z),...,a_n(z)) в систему с основанием  так, чтобы выполнилось условие

A(z)= a₁(z) ·B₁(z)+ a₂(z) · B₂(z) +...+ a_n(z) · B_n(z) (1)

где B_i(Z) - базисы системы;  i=1,2...,n.

В общем виде любой базис можно представить в непозиционном виде как

                (2)

где ; i, j=1,2...,n

С другой стороны известно, что любой элемент A(z)∈ Р(Z) можно представить как сумму ортогональных полиномов А₁(z),А₂(z),...,А_n(z), т.е.

A(z)=(a₁(z),a₂(z),...,a_n(z)) =А₁(z)+А₂(z)+... ...+А_n(z)=(a₁(z),0,..,0)+(0, a₂(z),0,..,0)+...          (3)

...+(0,0,... a_n(z))                

Под ортогональным полиномом понимается элемент расширенного поля GF(p^ν) заданного основаниями р₁(z),...,p_n(z) таких, что  , у которого все остатки равны нулю, за исключением цифры по модулю р_i (z)

А_i(z)=(0,0,...,0, а_i (z),0,...0), где  i=1,2...,n.

Приравнивая выражения (1) и (3) и учитывая независимость выполнения арифметических операций по модулям полиномиальной системы классов вычетов (ПСКВ), получаем, что

а_i (z) · B_i(z) =(0,0,...,0, а_i (z),0,...0).                                (4)

Исходя из условия представления базисов системы согласно (2)

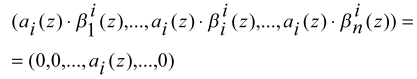(5)

Следовательно, ортогональные базисы B_i(z), i=1,2...,n системы ПСКВ расширенного поля Галуа GF(p^ν) можно представить в следующем виде

B₁(z) = ( 1,0,...,0,...,0);       

: 

   B_i(z) = ( 0,0,...,1,...,0);      (6)

:    

   B_n(z) = ( 0,0,...,0,...,1);  

Таким образом, выражение (1) можно записать как:

    (7)

Для получения значений ортогональных базисов ПСКВ воспользуемся КТО и равенствами (6), согласно которым

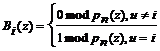         (8)

где

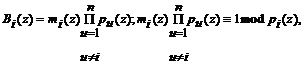
Преобразуя выражение (8), получаем формулу для вычисления ортогонального базиса по i-ому основанию

B_i(z) = m_i (z)×P(z)/ p_i(z),                     (9)

где - m_i (z) - вес ортогонального базиса.

Вес ортогонального базиса выбирается из условия B_i(z) mod p_i(z) ≡ 1.

Устройство обратного преобразования из ПСКВ, обладает высоким быстродействием - процедура перевода осуществляется за одну итерациюна основе нейронных сетей (НС) прямого распространения. Кроме того, данная структура характеризуется отсутствием выходного сумматора по модулю , а, следовательно, и обратных связей, что в значительной степени приведет к повышению быстродействия вычислительной структуры в целом [7,8].

СПИСОК ЛИТЕРАТУРЫ

1. Акушский И.Я., Юдицкий Д.М. Машинная арифметика в остаточных классах. - М.: Сов. Радио, 1968. - 440с
2. Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа. /Нейрокомпьютеры: разработка, применение. №6, 2003, с.61-68.
3. Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Архитектура отказоустойчивой нейронной сети для цифровой обработки сигналов /Нейрокомпьютеры: разработка, применение.№12, 2004, с.51-60.
4. Калмыков И.А. Лободин М.В., Гахов В.Р., Владимиров А.А. Высокоскоростной нейросетевой преобразователь из полиномиальной системы классов вычетов в позиционный код /Труды международного форума по проблемам науки, техники и образования. Том1. /Под ред. В.П. Савиных, В.В, Вишневского. - М.: Академия наук, 2004. - с.151-152.
5. Червяков Н.И. Преобразование цифровых позиционных и непозиционных кодов в системах управления и связи.- Ставрополь, СВВИУС, 1985. - 63 с.
6. Червяков Н.И., Сахнюк П.А., Шапошников А.В., Ряднов С.А.Модулярные параллельные вычислительные структуры нейропроцессорных систем. М.: ФИЗМАТЛИТ, 2003. - 288 с.
7. Элементы применения компьютерной математики и нейроинформатики/ Н.И. Червяков, И.А. Калмыков, В.А. Галкина, Ю.О. Щелкунова, А.АШилов; под редакцией Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216 с.
8. Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе класса вычетов. - М.: ФИЗМАТЛИТ, 2005. - 274 с.

Библиографическая ссылка