Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы

Иванов Е.М.

Показано, что работа растяжения пружины A>kx_m² , где k - жесткость пружины, x_m - максимальное растяжение. При вычислении работы  надо использовать значения x и dx, полученные из решения уравнения движения.

Статья в формате PDF

159 KB

Показано, что работа растяжения пружины A>kx_m² , где k - жесткость пружины, x_m - максимальное растяжение. При вычислении работы  надо использовать значения x и dx, полученные из решения уравнения движения.

It is shown, that work of a stretching of a spring A>kx_m²  , where k - rigidity of a spring, x_m - the maximal stretching. At calculation of work  it is necessary to use values x and dx, the equations of movement received from the decision.

Рассмотрим спиральную пружину, один конец которой закреплен (рис. 1а), а к другому прикреплен груз массой m. Если пружину растянуть или сжать, то возникает сила F, стремящаяся вернуть тело в положение равновесия. При небольших растяжениях x справедлив закон Гука - сила пропорциональна растяжению пружины: F = -kx. Постоянная k называется коэффициентом упругости, или жесткостью пружины. Знак минус означает, что сила F направлена в сторону, противоположную смещению x, т.е. к положению равновесия x = 0. Геометрически (рис. 1b) , k = tgβ, x_m - максимальное (амплитудное) растяжение пружины.

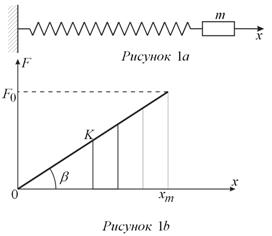
В курсах физики утверждается, что работа при растяжении от x = 0 до x_m будет равна

                  (1)

и эта работа равна потенциальной энергии пружины, растянутой (или сжатой) на величину x_m и обладающей жесткостью k. Однако это одно из заблуждений классической механики. Растягивающей силой, равной F = kx, нельзя растянуть пружину даже на долю микрона. Чтобы растянуть пружину, надо приложить растягивающую силу в виде (F₁ + k₁x ), где F₁ >0 (рис. 2а). Уравнение движения (II закон Ньютона) запишем в следующем виде:

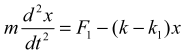                       (2)

Решение при нулевых начальных условиях (при t = 0, x =0 и V =0) имеет вид

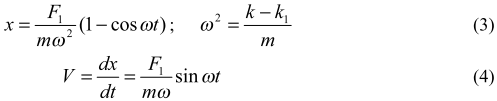
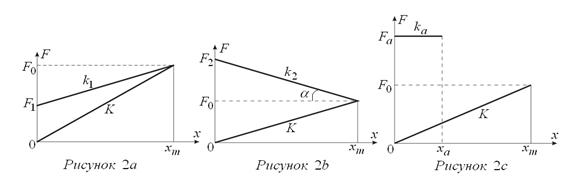
Из решения следует, что если F₁ =0, то растяжения пружины не происходит. Амплитудные значения (при x = x_m):

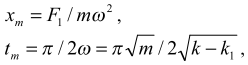
Работу вычисляем по формуле , где F = F₁ - (k - k₁)x, а x и dx определяются из выражений (3) и (4). Работа, совершаемая растягивающей силой

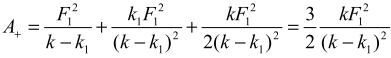      (5)

Работа, совершаемая силой упругости пружины

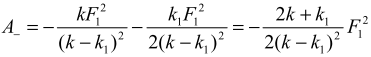            (6)

Из соотношения (5) следует, что работа, совершаемая растягивающей силой, не зависит от величин F₁ и k₁ и равна работе

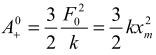          (5а)

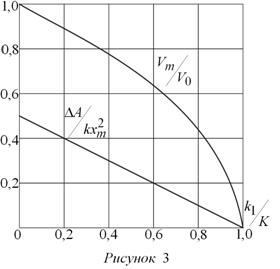
совершаемой постоянной силой F₀, при этом работа, совершаемая силой упругости пружины A_-⁰ = -kx_m² разность работ ΔA₀ = kx_m² / 2 , конечная скорость при  x = x_m На рис. 3 даны графики зависимостей V_m / V₀ и ΔA = kx_m² от величины отношения K₁ / K. ΔA - кинетическая энергия груза.

Рассмотрим случай растягивающей силы F_P > F₀ (рис.2b) F_P = F₂ + k₂x  = F₂ - b²x , где b² = -k₂ = tgα. Дифференциальное уравнение движения имеет вид:

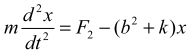                    (7)

Его решение при нулевых начальных условиях имеет вид:

 ;                 (8)

            (9)

Амплитудные значения (при x = x_m): x_m = F₂ / mω²; ; .

Работа, совершаемая растягивающей силой

            (10)

Работа, совершаемая силой упругости пружины

                  (11)

Кинетическая энергия груза при x = x_m

                 (12)

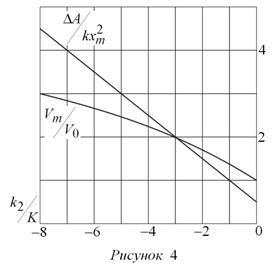
На рис. 4 даны графики изменения безразмерных комплексов ΔA / kx_m² и V_m / V₀ в зависимости от величины отношения k₂ / k.

Рассмотрим третий способ растяжения пружины с грузом (рис. 2с). Прикладываем растягивающую силу F_a >>F₀  для растяжения пружины на некоторое расстояние x_a, затем сила F_a отключается, а оставшийся отрезок пути, равный x_m - x_a, груз проходит по инерции, используя запас кинетической энергии K_a, приобретенный в точке x_a. Для первого участка пути дифференциальное уравнение имеет вид

             (13)

Его решение при нулевых начальных условиях:

;                 (14)

                    (15)

Время движения до x = x_a

               (16)

Работу вычисляем по формуле , где F(x) = F_a - kx, а x и dx определяются выражениями (14) и (15). Работа растяжения на участке до x = x₀

                                     (17)

Работа, совершаемая силой упругости пружины на этом же участке

            (18)

Кинетическая энергия, приобретенная грузом:

              (19)

Для второго участка уравнение движения имеет вид

                (20)

Начальные условия для этого уравнения примем в виде: при t = 0 координата x = x_a, скорость V_a определяется выражением (15) при t = t_a. Решение будет иметь вид:

                   (21)

           (21a)

Работа силы упругости пружины на участке от x = x_a до x_m определится интегралом , где x и dx определяются выражениями (21) и (21а):

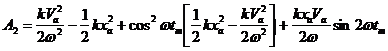        (22)

где t_m ─ время движения груза от x=x_a до x = x_m. Условием достижения этой точки является равенство начальной кинетической энергии K_a работе силы упругости пружины A₂. Это равенство сводится к трансцендентному уравнению

             (23)

где a = kx_a² / 2; b = K_a - a; c = kx_aV_a / 2ω; φ = ωt_m.

Приведем численный пример. Груз массой m = 1 кг, прикрепленный к пружине с жесткостью k = 400 Н/м, растягивается силой F₀ = 80 Н на расстояние x_m = 0,2. Работа силы растяжения  Дж, работа силы упругости пружины  Дж, время t = 0,0785 с.

Проведем растяжение силой F_a по схеме, показанной на рис. 2с. Расчет сведем в таблицу 1.

Таблица 1.

Таким образом, только в случае растяжения пружины с грузом по схеме, показанной на рис.2с, можно затратить работу на растяжение A₊, близкую к потенциальной энергии растянутой пружины П = kx_m² / 2.

Библиографическая ссылка