Одним из наиболее изученных металлооксидных купратов является иттриевая керамика ![]() . Получение материала
. Получение материала ![]() (
(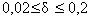 ) в виде порошка, минуя стадию брикетирования, обладающего TC не менее 88 К и
) в виде порошка, минуя стадию брикетирования, обладающего TC не менее 88 К и ![]() , с содержанием сверхпроводящей фазы не менее 90% представляет важную практическую задачу. Независимо от метода получения сложного оксида, для обеспечения сверхпроводящих свойств эти соединения должны иметь определенную структуру. Наличие структурных микродефектов, химических неоднородностей значительно ухудшает электронные и магнитные свойства сверхпроводников, поэтому попытка модификации таких материалов должна быть направлена на устранение указанных недостатков.
, с содержанием сверхпроводящей фазы не менее 90% представляет важную практическую задачу. Независимо от метода получения сложного оксида, для обеспечения сверхпроводящих свойств эти соединения должны иметь определенную структуру. Наличие структурных микродефектов, химических неоднородностей значительно ухудшает электронные и магнитные свойства сверхпроводников, поэтому попытка модификации таких материалов должна быть направлена на устранение указанных недостатков.
Весьма перспективным методом получения порошков со сферической формой частиц является ионообменный. Такой способ был рекомендован [3] для получения ядерного топлива на основе оксида урана в виде микросфер.
В настоящей работе рассматривается способ получения порошков купратов иттрия и бария с использование метода ионного обмена на карбоксильном катионите КБ-4п-2. В данном случае порошки получались без операции брикетирования. Это достигалось получением на начальных стадиях композиционного материала «ионит - сорбированные ионы». Затем полученный материал подвергался термической обработке.
Целью работы являлось определения условия синтеза композиции «ионит - сорбированные ионы» с определенным соотношением между сорбированными ионами металлов иттрия, бария и меди - 1:2:3.
Расчеты проводились по программе составленной в среде математического пакета «MathCAD 14»
Экспериментальная часть
Для получения купрата иттрия и бария с заданным соотношением сорбируемых ионов в качестве основных факторов были выбраны концентрации иттрия (c1 ), концентрация бария (c2 ) и концентрация иттрия (c3 ). Параметром оптимизации или функцией отклика было значение сорбируемости или обменной емкости катионита по исследованным ионам. Значения базисных уровней:c01 = 0,03 ;c02 = 0,08 ;c03 = 0,07 ; интервал варьирования Δc1 = 0,01; Δc2 = 0,04 ;Δc3 = 0,02 .
В используемом методе математического планирования эксперимента применяются безразмерные кодированные композиционные факторы x1 и x2. Для перехода от концентрации ионов к соответствующим кодированным величинам применялись следующие формулы [2].
|
|
(1) |
В эксперименте реализован план 23. Использовался центральный композиционный план, отвечающий требованию рототабельности, т.е. план, позволяющий получать модель, способную предсказать значение параметра оптимизации с одинаковой точностью, независимо от направления на равных расстояниях от центра плана [1]. В таких условиях можно установить эмпирические уравнения регрессии, включающие линейные и нелинейные члены:
|
|
(2) |
Условия опытов, матрица планирования и результаты о совместной сорбции катионов иттрия, бария и меди карбоксильным катионитом КБ-4п-2 представлены в табл. 1.
обсуждение результатов
Коэффициенты регрессии bi были вычислены с помощью уравнений, приведенных в [2]. С применением критерия Стьюдента была проверена значимость этих коэффициентов с доверительной вероятностью 95%. Приведенные ниже сокращенные уравнения выражают зависимость параметров оптимизации от значений основных факторов:
|
|
(3) |
|
|
(4) |
|
|
(5) |
Чтобы проверить адекватность этих уравнений, были проведены 6 дополнительных опытов в центре плана. С помощью критерия Фишера была проверена адекватность полученных уравнений. Установлено, что на 5% процентном уровне значимости уравнения адекватно описывают экспериментальные данные.
Для получения сложного оксида на основе Y-Ba-Cu-O необходимо, чтобы в результате сорбции ионов иттрия, бария и меди на катионите выполнялось мольное соотношение Y:Ba:Cu = 1:2:3. Анализ уравнений делает очевидным, что увеличение параметра оптимизации необходимо перемещение в факторное пространство от центра плана по направлению, которое соответствует одновременному увеличению всех основных факторов. После применения метода крутого восхождения были получены оптимальные значения факторов для иттрия, бария и меди x1 = 0,2,x2 = 1,825 ,x3 = 0,3 .
На основании анализа уравнений можно заключить:
Таблица 1. Матрица планирования и результаты опытов по совместной сорбции ионов иттрия, бария и меди катионитом КБ-4п-2
|
Условия опытов |
x1 |
x2 |
x3 |
y1 |
y 2 |
y3 |
|
Концентрация, |
Г, моль Me n+ /г |
|||||
|
Y |
Ba |
Cu |
Y |
Ba |
Cu |
|
|
Основной уровень (xi = 0 ) |
0,03 |
0,08 |
0,07 |
|
|
|
|
Интервал варьирования (Δxi ) |
0,01 |
0,04 |
0,02 |
|||
|
Верхний уровень (xi =+1 ) |
0,04 |
0,04 |
0,05 |
|||
|
нижний уровень (xi = -1 ) |
0,02 |
0,12 |
0,09 |
|||
|
верхнее звездное плечо α=1,682 |
0,047 |
0,147 |
0,104 |
|||
|
нижнее звездное плечо α=-1,682 |
0,013 |
0,013 |
0,036 |
|||
|
№ |
|
|||||
|
1 |
+ |
+ |
+ |
0,467 |
0,2 |
1,175 |
|
2 |
- |
+ |
+ |
0,2 |
0,275 |
1,625 |
|
3 |
+ |
- |
+ |
0,4 |
0,6 |
1,2 |
|
4 |
+ |
+ |
- |
0,533 |
0,5 |
0,7 |
|
5 |
- |
- |
- |
0,5 |
0,25 |
1,2 |
|
6 |
+ |
- |
- |
0,517 |
0,15 |
0,725 |
|
7 |
- |
+ |
- |
0,417 |
0,775 |
1,25 |
|
8 |
- |
- |
+ |
0,317 |
0,175 |
1,625 |
|
9 |
α |
0 |
0 |
0,617 |
0,325 |
0,8 |
|
10 |
-α |
0 |
0 |
0,317 |
0,275 |
1,6 |
|
11 |
0 |
α |
0 |
0,35 |
0,65 |
1,125 |
|
12 |
0 |
-α |
0 |
0,517 |
0,425 |
1,2 |
|
13 |
0 |
0 |
α |
0,4 |
0,3 |
1,55 |
|
14 |
0 |
0 |
-α |
0,65 |
0,35 |
0,8 |
|
15 |
0 |
0 |
0 |
0,433 |
0,25 |
1,2 |
|
16 |
0 |
0 |
0 |
0,483 |
0,1 |
1,275 |
|
17 |
0 |
0 |
0 |
0,45 |
0,175 |
1,175 |
|
18 |
0 |
0 |
0 |
0,45 |
0,2 |
1,15 |
|
19 |
0 |
0 |
0 |
0,467 |
0,175 |
1,15 |
|
20 |
0 |
0 |
0 |
0,483 |
0,225 |
1,125 |
-
Зависимости сорбции иттрия и бария от основных факторов имеют экстремальный характер, поскольку квадратичные эффекты (b12 ,b13 ,b23 ) отличаются от нуля. Следовательно, поверхности отклика имеют так называемые «особые точки» (s),что указывает на существенное искривление поверхностей.
- Отличие от нуля b12 и b13 для сорбции иттрия и b13 и b23 для сорбции бария говорит о значительном взаимодействии основных факторов. Это указывает на то, что влияние концентрации иттрия на его сорбцию существенно зависит от концентрации бария и меди, а влияние концентрации меди на сорбцию бария зависит от концентраций иттрия и бария. Положительное значение этих факторов говорит о том, что их взаимодействие усиливает сорбцию иттрия, а взаимодействие бария и меди приводит к снижению сорбции бария.
- Для сорбции меди коэффициенты b12, b13 ,b23 равны нулю. Это говорит о том, что поверхность отклика не имеет центра, оптимум будет лежать на границе области определения факторов.
- Анализируя коэффициенты b1, b2 ,b3 можно сказать, что сорбцию иттрия можно увеличить, увеличив концентрацию иттрия и уменьшив концентрации бария и меди. Сорбцию бария можно увеличить, увеличив концентрации иттрия и бария и уменьшив концентрацию меди. Сорбцию меди можно усилить, уменьшив концентрацию иттрия и увеличив концентрацию меди.
- Коэффициенты b0 равные средним значениям факторов сорбции ионов в центре плана возрастают в ряду Cu>Y>Ba, что согласуется с размерами гидратированных радиусов ионов.
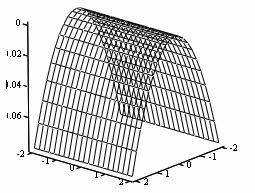
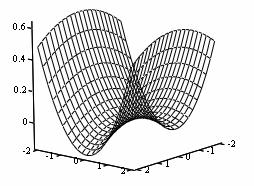
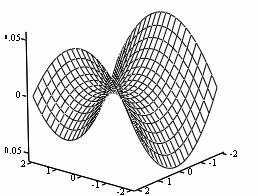
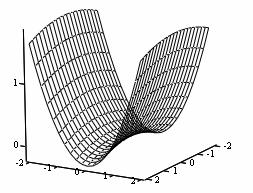
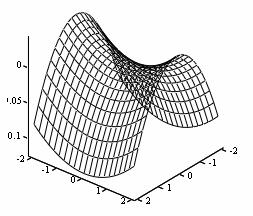
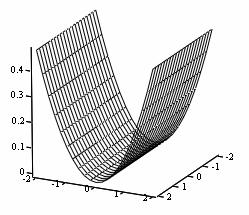
Уравнения регрессии второго порядка, адекватно описывающие почти стационарную область, несут в себе обширную информацию о влиянии основных факторов на отклик. Однако для получения целостной картины зависимости сорбции от концентрации ионов представляет интерес изучение свойств поверхностей откликов (рис. 1).
|
Сорбция иттрия |
Сорбция бария |
|
|
|
|
|
|
|
|
|
Рис. 1. Геометрический образ поверхности отклика y1 =f(X1,X2), определяемой уравнением (6): а * x1 =0,2 , б * x2 =1,825 , в *x3 =0,3
При этом полезно перейти от полинома второго порядка, полученного по результатам опыта, к стандартному каноническому уравнению:
|
|
(6) |
где ys - значение выхода в центре поверхности; X1 и X2 - канонические переменные, являющиеся линейными функциями факторов x1 и x2; λ11 и λ22 - коэффициенты канонической формы.
Параметры λ11 и λ22 в уравнении (6) определяют вид поверхностей откликов, которые классифицируются по их каноническим формам.
Для исключения линейных членов (b0 ) в уравнениях регрессии начала координат в факторном пространстве были перенесены в «особые точки», затем координатные оси повернуты таким образом, чтобы в уравнениях исключить члены двойного взаимодействия ( b12, b13 ,b23 ) [4].
Т.к. в уравнения регрессии описываются при помощи трех факторов, приходится решать компромиссную задачу - определять экстремальные значения функции отклика при ограничениях, принимая попеременно оптимальные значения факторов. Полученные значения представлены в табл. 2.
Таблица 2. Значения канонических коэффициентов, рассчитанных для сорбции иттрия и бария
|
Сорбция иттрия |
Ион, значения которого приняты постоянными |
λ11 |
λ22 |
Сорбция бария |
λ11 |
λ22 |
|
x1 =0,2 , иттрий |
-0,02 |
0 |
-0,036 |
0,156 |
||
|
x2 = 1,825 барий |
-0,0135 |
0,0135 |
-0,0455 |
0,0455 |
||
|
x3 = 0,3 медь |
-0,03 |
0,01 |
0 |
0,12 |
Для сорбции иттрия при постоянной его концентрации и сорбции бария при постоянной концентрации меди коэффициент Л11=0. Это говорит том, что центр лежит далеко за областью экспериментирования. Поверхности такого типа называются «возрастающим возвышением».
В остальных исследуемых системах коэффициенты λ11 и λ22 имеют разные знаки, это означает, что поверхность отклика - гиперболический параболоид. В центре поверхности - минимакс. Поскольку λ11<λ22 , то влияние основных факторов на сорбцию характеризуется неаддитивностью действия.
Заключение
В результате проведенных исследований получены уравнения регрессии для сорбции ионов иттрия, меди и бария в зависимости от концентрации ионов. Показаны возможности метода полного факторного эксперимента.
Список литературы
- Адлер Ю.П. Введение в планирование эксперимента. - М.: Металлургия - 1969. - 157 с.
- Ахназарова С.Л. Кафаров В.В. Методы оптимизации эксперимента в химической технологии. М.: Высшая школа, 1985. 327с.
- Бек М. Химия равновесных реакций комплексообразования. - Пер. с анг. М.: Мир. - 1973. - 358 с.
- Рухадзе М.Д., Безарашвили Г.С., Сидамонидзе Ш.И., Кутхашвили М.Г.// Журн. физ. химии. 1998. Т.72. №11. С. 2055.
Библиографическая ссылка
Пимнева Л.А., Нестерова Е.Л. ОПТИМИЗАЦИЯ ПРОЦЕССА ПОЛУЧЕНИЯ КУПРАТА ИТТРИЯ И БАРИЯ ТЕРМОЛИЗОМ КАТИОНИТА КБ-4П-2 С ИСПОЛЬЗОВАНИЕМ МЕТОДА МАТЕМАТИЧЕСКОГО ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА // Современные наукоемкие технологии. 2010. № 1. С. 21-26;URL: https://top-technologies.ru/ru/article/view?id=24360 (дата обращения: 05.03.2026).




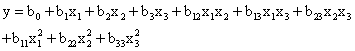
 а
а
 а
а
 б
б
 б
б
 в
в
 в
в