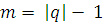Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы

Сергиенко Л.С. Грицких И.В.

Предлагается один из вариантов структурно-логической схемы исследования числовых рядов с применением ЭВМ.

Статья в формате PDF

298 KB

Как следствие произошла и коренная перестройка в сфере образования. Возможность манипулировать огромными объёмами информации, в считанные минуты решать сложные задачи с большим количеством компонентов и многие другие виртуальные возможности вычислительной техники естественным образом изменили систему образования, повысили её потенциальные возможности.

В настоящее время проходят стадию эксперимента многие новые компьютерные технологии образования - например, дистанционная (заочная) форма обучения. При этом одной из первоочередных задач становится развитие у пользователей способностей быстро усваивать и эффективно оперировать полученными знаниями, умение их идентифицировать и оптимальным образом систематизировать в блоки, устанавливать внутренние и внешние структурно - логические связи.

Приведём пример определения функциональной зависимости между различными блоками учебного материала по теории рядов.

Структурно-логическая схема исследования числовых рядов

Рассмотрим один из вариантов представления некоторых основных положений теории числовых рядов в виде последовательности применения признаков сходимости. Алгоритмическая схема содержит три взаимосвязанных блока:

• Р1 - предельные признаки сходимости;
• Р2 - теоремы сравнения;
• Р3 - признаки сходимости знакопеременных рядов.

1. Предельные признаки сходимости

Первая блок-схема охватывает необходимый и достаточные признаки сходимости: признак Даламбера, радикальный и интегральный признаки Коши.

Расшифровка операторов A₁ ÷A₁₇ блок - схемы Р1 представлена в табл. 1, смысл логических условий a₁÷ a₁₃ приведён в табл. 2.

Рис. 1. Схема Р1 алгоритма исследования рядов с помощью предельных признаков сходимости

Таблица 1. Операторы алгоритма 1

Сразу после введения исследуемого ряда по виду его общего члена определяется, не является ли данный ряд геометрическим или гармоническим рядом. При положительном ответе по соответствующим значениям определённых параметров легко устанавливается сходимость или расходимость ряда и процесс исследования заканчивается. В противном случае проверяется, все ли члены ряда положительны - если нет, то необходимо перейти к третьему блоку Р3 схемы исследования знакопеременных рядов.

Если же исследуемый ряд знакопостоянный, то проверяется соблюдение необходимого признака сходимости. При его нарушении ряд расходится, а при выполнении процесс исследования продолжается дальше.

Если по признаку Даламбера или радикальному признаку Коши не удаётся решить вопрос о сходимости или расходимости данного ряда, то применяется интегральный признак Коши. В случае, когда первообразную или предел при вычислении несобственного интеграла первого рода определить не удаётся, необходимо перейти ко второму блоку схемы исследования рядов с положительными членами по теоремам сравнения.

Таблица 2. Логические условия алгоритма 1

2. Теоремы сравнения

Во второй блок - схеме Р2 обозначен алгоритм исследования сходимости числовых рядов с положительными членами с помощью признаков сравнения. Вместе с исследуемым рядом вводится по возможности близкий к нему ряд, сходимость или расходимость которого установлена заранее. В качестве такого ряда, как правило, выбирают, если это приводит к положительному результату, геометрический или гармонический ряд. Если ряд с известной сходимостью или расходимостью для данного ряда удаётся подобрать, то в схеме сначала используется первый предельный признак сравнения. В случае, когда предел отношения сравниваемых на бесконечности общих членов рядов равен отличной от нуля постоянной величине, оба ряда одновременно сходятся или расходятся. Если же этот предел не существует (не определяется или равен бесконечности), то обращаются ко второй теореме сравнения с помощью неравенств.

При выполнении для всех членов ряда, начиная с некоторого фиксированного номера, неравенств одинакового смысла в случае расходимости минорантного ряда исследуемый ряд тоже разойдётся, а при сходимости мажорантного ряда - сойдётся. Если же выполнение обозначенных неравенств не доказано, необходимо вернуться к началу алгоритма 2 и ввести какой-либо другой ряд с известной сходимостью и повторить процесс сравнения. В случае, когда такой ряд найти не удаётся, исследование сходимости данного ряда рассмотренными в построенной схеме методами не удаётся.

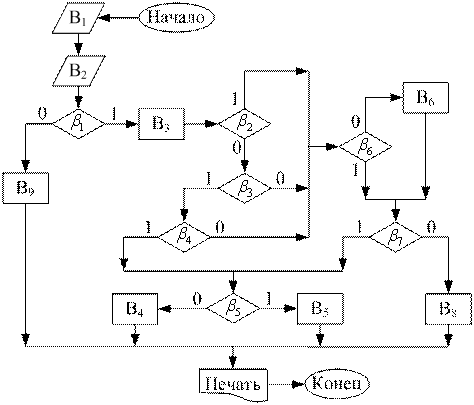
Рис. 2. Схема Р2 алгоритма исследования сходимости рядов по теоремам сравнения

Таблица 3. Операторы алгоритма 2

Расшифровка использованных в блок - схеме Р2 на рис. 2 операторов  дана в табл. 3, смысл логических условий  приведён в табл. 4.

Таблица 4. Логические условия алгоритма 2

3. Признаки сходимости знакопеременных рядов

Рис. 3. Схема Р2 алгоритма исследования знакопеременных рядов

Таблица 5. Операторы алгоритма 3

На рис. 3 представлена блок - схема Р3 алгоритма исследования знакопеременных рядов с расшифровкой обозначений C1 ÷ C7 и Y1 ÷ Y5 в табл. 5 и табл. 6.

Таблица 6. Логические условия алгоритма 3

Третья блок-схема включает два признака сходимости: признак Лейбница для знакочередующихся рядов и достаточный признак сходимости для знакопеременных рядов. Если исследуемый ряд знакочередующийся и нарушается первое условие теоремы Лейбница о монотонном убывании абсолютных величин его членов, то ряд может как сходиться, так и расходиться. При выполнении обозначенного требования и невыполнении второго условия признака Лейбница - равенства нулю предела модуля общего члена ряда на бесконечности - поведение ряда так же неизвестно.

Если оба условия признака Лейбница выполнены, то устанавливается характер сходимости ряда: сходится ряд условно или абсолютно. Для этого определяется поведение ряда из абсолютных величин членов знакочередующегося ряда - если ряд из модулей сходится, то исследуемый ряд абсолютно сходится, если нет - исследуемый ряд сходится условно.

Если исследуемый знакопеременный ряд не является знакочередующимся рядом, то в случае сходимости ряда из его модулей он сходится абсолютно.

Вывод

Наличие блок - схемы алгоритма позволяет представить процедуры усвоения необходимой информации и определения правильного решения в виде конечной последовательности функционально - логических операций. Формализация системы образования существенно упрощает процесс обучения и способствует более глубокому и быстрому усвоению изучаемого материала.

СПИСОК ЛИТЕРАТУРЫ:

1. Воробьёв Н.Н. Теория рядов. - М.: Наука, 2006. - 408 с.
2. Сергиенко Л.С. Основы теории числовых рядов. - Иркутск: Ир ГТУ, 2008. - 65 с.

Библиографическая ссылка