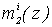Решение проблемы исследований: Качественно новые требования, предъявляемые к цифровой обработке сигналов (ЦОС), а также всестороннее применение методов ЦОС, обусловили повышенный интерес к применению вычислительных систем, построенных на основе алгебраических систем, обладающих свойством конечного кольца или поля. Особое место среди них занимает полиномиальная система классов вычетов в расширенных полях Галуа GF(2v).
Малоразрядность остатков и независимость их обработки служат идеальной основой для построения высокоскоростных вычислительных систем ПСКВ [1,2]. В данной системе полином A(z) представляется в виде
, (1)
где 
, рi(z) - минимальный многочлен поля Галуа;
.
Наряду с высоким быстродействием, обусловленным малоразрядностью остатков и модульностью вычислений, ПСКВ обладает способностью обеспечивать живучесть вычислительным системам. Если на диапазон возможного изменения кодируемого множества M(z) наложить ограничения, считая, что для однозначного представления достаточно k первых остатков (k < n), то соответствующие им основания упорядоченной системы 
принадлежат множеству информационных модулей. В этом случае диапазон однозначного представления по данным основаниям соответственно равен 
. Оставшиеся «лишние остатки» r = n - k считаются избыточными. Изменяя количество информационных k и избыточных r оснований в заданной структуре непозиционного СП, можно варьировать его основные показатели - точность, информационная надежность и производительность [1,3,4,5].
Возникновение ошибки в непозиционной кодовой конструкции A(z) переводит ее из подмножества разрешенных комбинаций в подмножество запрещенных. Согласно КТО значение ошибочного полинома A*(z) определяется
. (2)
Анализ выражения (1) показывает, что местоположение ошибочного полинома A*(z) относительно рабочего диапазона Pраб(z) определяется величиной второго слагаемого.
Известно [3,4,5] , что величина ортогонального основания определяется
, (3)
где mj(z) - вес ортогонального j -го базиса.
С другой стороны, должно обеспечиваться условие
. (4)
Преобразовав выражение (3), получаем
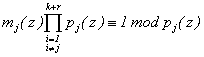. (5)
Разделив обе части равенства (5) на величину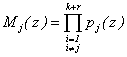 
, получаем
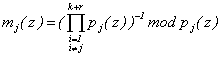. (6)
Принимая во внимание попарную простоту модулей pi(z), i=1, 2, ..., k+r, введем обозначение
.
Тогда
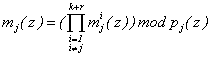. (7)
Полученное значение веса ортогонального базиса может быть использовано для вычисления интервального номера, в который попадает ошибочный полином, из условия
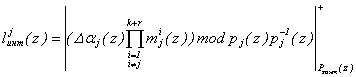, где 
(8)
Пример. Пусть задана полиномиальная система класса вычетов поля GF(24). В данной системе определены следующие минимальные многочлены:
р1(z)=z+1; р2(z)=z2+z+1; р3(z)=z4+z3+z2+z+1; р4(z)=z4+z3+1; р5(z)=z4+z+1.
В качестве контрольного основания используется основание 
. Тогда 
. Пусть ошибка произошла равна 
. Тогда
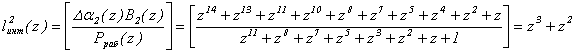
Воспользуемся (8) для вычисления l2 инт. Значения mi j (z) для оснований ПСКВ поля GF(24) представлены в таблице 1.
Таблица 1. Величины для поля GF(24)
|
|
Значение рi(z) основания ПСКВ |
||||
|
p1(z) |
p2(z) |
p3(z) |
p4(z) |
p5(z) |
|
|
|
- |
1 |
1 |
1 |
1 |
|
|
z |
- |
z |
z+1 |
1 |
|
|
z3+z |
z3+1 |
- |
z2+1 |
z3+z2+1 |
|
|
z3 |
z3+z2+z |
z2 |
- |
z3+z+1 |
|
|
z3+z2+z |
z2+z |
z3+z |
z3+z2 |
- |
Тогда имеем 
Подставляя в равенство (8), получаем:
.
Таким образом, очевидно, что применение математической модели вычисления интервального номера, согласно (13), позволяет обнаружить в коде все однократные ошибки даже при постепенной деградации структуры СП ПСКВ.
Выводы:
Проведенные исследования позволили доказать связь между размещением ошибочных полиномов по диапазону при деградации структуры вычислительной системы и величинами весов ортогональных базисов ПСКВ. Разработана математическая модель контроля и коррекции ошибок для непозиционных спецпроцессоров ЦОС, функционирующих в ПСКВ.
Cписок литературы:
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/ Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с
- Элементы применения компьютерной математики и нейроинформатики/Н.И. Червяков, И.А. Калмыков И.А., В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216 с.
- Калмыков И.А., Щелкунова Ю.О., Гахов В.Р., Шилов А.А. Математическая модель коррекции ошибок в полиномиальной системе класса вычетов на основе определения корней интервального полинома.// Физика волновых процессов и радиотехнические системы. - Т. 6. - №5. - С. 30-34.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований сигналов в расширенных полях Галуа// Нейрокомпьютеры: разработка и применение. - 2003. - №6. - С.61-68.
- Калмыков И.А. ,Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронной сети для коррекции ошибок в непозиционном коде расширенного поля Галуа// Нейрокомпьютеры: разработка и применение. - 2003. - №8-9. - С.10-1
Работа представлена на заочную электронную конференцию «Прикладные исследования и разработки по приоритетным направлениям науки и техники», 15-20 января 2008 г. Поступила в редакцию 01.07.2008.
Библиографическая ссылка
Калмыков И.А., Руденко А.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПРЕДЕЛЕНИЯ ИНТЕРВАЛЬНОГО НОМЕРА ПОЛИНОМА ПРИ ДЕГРАДАЦИИ СТРУКТУРЫ НЕПОЗИЦИОННОГО ПРОЦЕССОРА // Современные наукоемкие технологии. – 2008. – № 7. – С. 95-97;URL: https://top-technologies.ru/ru/article/view?id=24078 (дата обращения: 03.12.2024).