Пусть граница ACDB катода отделена от границы AB (L4z) анода зазором, в котором осуществляется течение электролита. Течение электролита осуществляется в направлении от входа в межэлектродный промежуток в окрестности точки А слева к точке В. ( A и B - бесконечноудаленные точки).
Прямолинейные полубесконечные участки границы катода AC (L1z) и DB (L3z) образуют с горизонтальной осью абсцисс углы 
и 
соответственно. Участок катода CD (L2z), на котором скорость должна быть постоянной и равна V0, и граница анода AB, на которой 
( V - модуль, θ - угол наклона вектора скорости к оси OX), a,b - постоянные [2] , неизвестны.
Для решения задачи введем вспомогательное комплексное переменное 
, изменяющееся в прямоугольнике 
) и будем искать функцию z(u), конформно отображающую область Du на область течения в плоскости z = x + iy таким образом, чтобы границам анода и криволинейного участка катода CD соответствовали горизонтальные стороны прямоугольника, а участкам границ AC и BD - вертикальные (анод - 
; AC - ξ = 0).
Выражение функция 
(см [2]) имеет вид:
,
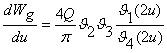где Wg - потенциал гидродинамического поля течения, 
- тэта функции для периодов 
и 
, 
- расход жидкости в струе, VA - скорость потока, 
безразмерная величина межэлектродного зазора на бесконечности в точке А.
Рассмотрим граничные условия для функции Жуковского:
. (1)
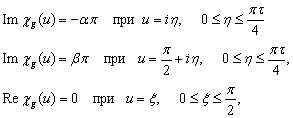(2)
На анодной границе функция Жуковского удовлетворяет следующему граничному условию
, (3)
где W(u) - комплексный потенциал электростатического поля
Функция W(u) удовлетворяет следующим граничным условиям
, 
(4)
Функцию dW/du можно построить, используя метод особых точек
. (5)
Подставляя (1), (5), в (3), получим:
. (6)
Таким образом, функция 
на границе Lu должна удовлетворять условиям (2) и (6).
Для использования метода Леви-Чивита [1] рассмотрим задачу о плоском течении идеальной жидкости по схеме, когда на границе анода L4z значение скорости постоянное и равно V*A, и будем искать функцию в виде суммы
, (7)
где Ω(u) - аналитическая в Du и непрерывная в 
функция. Учитывая граничные условия (2), будем искать 
можно представить в виде:
, (8)
а неизвестную функцию Ω(u) с вещественными коэффициентами an можно представить в виде ряда:
, (9)
Из (8) получим:
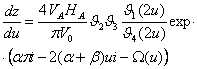. (10)
где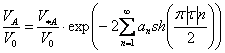 
. (11)
Для численного решения задачи задаются углы , 
и математический параметр 
. Коэффициенты разложения (9) определяются из уравнения (6). Значение параметра VA / V0, характеризующего режим течения, определяется из (11), а неизвестные границы находятся из соотношения (10).
СПИСОК ЛИТЕРАТУРЫ
- Киселев О.М., Котляр Л.М. Нелинейные задачи теории струйных течений тяжелой жидкости. Изд. Казанского университета, 1978.
- Котляр Л.М., Миназетдинов Н.М. Определение формы анода с учетом свойств электролита в задачах электрохимической размерной обработки металлов.//ПМТФ, 2003, Т.44, 143, с.179-184.
Библиографическая ссылка
Котляр Л.М., Миназетдинов Н.М., Хайруллин А.Х. ПРОЕКТИРОВАНИЕ «БЕЗКАВИТАЦИОННОГО» КАТОДА В ЗАДАЧАХ ЭЛЕКТРОХИМИЧЕСКОЙ ОБРАБОТКИ МЕТАЛЛА // Современные наукоемкие технологии. – 2005. – № 8. – С. 37-39;URL: https://top-technologies.ru/ru/article/view?id=23458 (дата обращения: 04.12.2024).