Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Синько Г.И.

Статья в формате PDF

160 KB

,                           (1)

где - самосопряженное дифференциальное выражение с вещественным и суммируемым коэффициентом q(x) таким, что для любого b>0  ,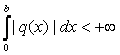

а 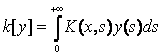 - интегральное выражение с ненулевым вещественным симметрическим ядром Гильберта-Шмитда K(x,s) удовлетворяющее условиям:

а) для любых решений  уравнения  

;

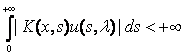б) в окрестности вещественной оси существует и регулярно по λ решение однородного и.-д. уравнения .

Операцией l в  порождается квазидифференциальный оператор L с минимальной областью определения D_L.

Обозначим через A = L + K и.-д. оператор, порождаемый и.-д. выражением (1) с минимальной областью определения D_A = D_L, где .

В работе рассматривается случай индекса дефекта (1.1).

Пусть  - произвольное фиксированное невещественное число, а F - линейный оператор, действующий из дефектного подпространства  в .

Квазисамосопряженным расширением оператора F, определяемым ограниченным оператором F, называется оператор A_F, заданный на множестве

равенством

,

а совокупность всех обобщенных резольвент R_λ оператора A определяется равенством (см. [1])

  ,

где  - произвольная регулярная в полуплоскости операторная функция из дефектного подпространства  в , не превосходящая единицы по норме, а  - квазисамосопряженное расширение оператора A, определяемое оператором . Были доказаны следующие утверждения.

Теорема 1. Область определения  квазисамосопряженного расширения  и.-д. оператора A есть совокупность всех тех функций , которые удовлетворяют граничному условию

  ,                  (2)

где  - произвольная регулярная в верхней полуплоскости функция с неотрицательной мнимой частью, или обращается в бесконечность. При этом формулой (2) определяется самосопряженные расширения и.-д. оператора A в пространстве  тогда и только тогда, когда  есть вещественная постоянная или обращается в бесконечность. Соответствие между классом операторных функций F(λ) и классом функций  взаимно однозначно.

Пусть  - произвольная функция из , тогда имеет место

Теорема 2. Совокупность всех обобщенных резольвент R_λ  и.-д. оператора A при любом невещественном λ является интегральным оператором

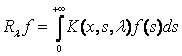                           (3)

с ядром ,

где  - произвольная регулярная в верхней полуплоскости функция с неотрицательной мнимой частью, или обращается в бесконечность. При этом различным функциям  соответствуют различные обобщенные резольвенты. Формулой (3) определяется резольвента самосопряженного расширения в пространстве  и.-д. оператора A тогда и только тогда, когда  есть вещественная постоянная или обращается в бесконечность.

Здесь  - решение однородного и.-д. уравнения, удовлетворяющее условиям  и , а функция , зависящая от решения однородного и.-д. уравнения регулярна в верхней полуплоскости и имеет там положительную мнимую часть. Ядро  выражается через резольвенту некоторого самосопряженного расширения дифференциального оператора L для некоторого элемента, зависящего от  из .

Построения всех формул обобщенных резольвент конечномерного возмущения дифференциальных операторов можно найти в работе [2].

СПИСОК ЛИТЕРАТУРЫ

1. Штраус А.В. Обобщенные резольвенты симметрических операторов // Изв. АН СССР, серия математическая, 1954,- Т.18. №1.- с.51-86.
2. Синько Г.И. Спектральная теория интегро-дифференциальных операторов в гильбертовом пространстве.- Уссурийск: Изд-во УГПИ, 1999. 151с.

Библиографическая ссылка