Введение
Растущая потребность в устойчивых энергетических решениях в последние годы обусловила повышенный интерес к солнечной энергии. Однако эффективность традиционных солнечных тепловых коллекторов пока уступает конкурирующим технологиям, что стимулирует поиск путей их совершенствования. Одним из перспективных направлений выступает применение наножидкостей – суспензий наночастиц в базовой жидкости – в качестве теплоносителя в коллекторах прямого поглощения (НКПП) [1; 2]. Такие системы совмещают поглощение солнечного излучения и его транспортировку, что потенциально повышает общую эффективность преобразования энергии [3].
Для оптимизации НКПП необходимы детальные исследования распределения солнечного излучения внутри рабочего объема и его зависимости от оптических свойств как базовой жидкости, так и наночастиц. Математическое моделирование позволяет эффективно анализировать эти процессы, сокращая затраты на экспериментальную отработку конструкций [4]. В литературе уже предложены модели, учитывающие влияние объемной доли наночастиц, геометрии коллектора и условий течения на тепловую производительность [5]. Вместе с тем, несмотря на активные исследования, промышленное внедрение НКПП сдерживается проблемами стабильности наножидкостей, их стоимости и недостаточной предсказуемости характеристик в реальных условиях [6]. В связи с этим численный анализ распределения интенсивности солнечного излучения в НКПП остается актуальной задачей, которой и посвящена настоящая работа.
Цель исследования – разработка математической модели, описывающей процессы тепломассопереноса в наножидкостном солнечном коллекторе прямого поглощения при установившемся течении рабочей среды с учетом температурной зависимости динамической вязкости наножидкости, а также численное исследование влияния параметров наножидкостей на характеристики солнечного коллектора.
Материалы и методы исследования
В работе рассматривается плоский солнечный коллектор прямого поглощения, заполненный наножидкостью на основе этиленгликоля с диспергированными наночастицами алюминия. Выбор этиленгликоля в качестве базовой жидкости обусловлен его выраженной температурной зависимостью теплофизических свойств, в частности динамической вязкости, что позволяет более полно учесть нелинейные эффекты при моделировании тепломассопереноса [7, с. 253–281].
Математическая модель основана на уравнениях теплопроводности, стационарного уравнения Навье – Стокса и уравнения несжимаемости. Поглощение солнечного излучения наножидкостью описывается на основе закона Бугера – Ламберта – Бера, согласно которому ослабление интенсивности излучения определенной длины волны λ при прохождении через поглощающую среду моделируется обыкновенным дифференциальным уравнением первого порядка. Соответствующая задача формулируется как задача Коши, а суммарное значение величины интенсивности излучения вычисляется интегрированием по всему спектру излучения [8].
Температурная зависимость динамической вязкости μ(Т) задается посредством аппроксимации экспериментальных значений с применением метода наименьших квадратов и подбора вида аппроксимационных функций, а также методов регрессионного и интерполяционного анализа.
Граничные условия включают:
– заданную скорость на входе в коллектор;
– условия прилипания на твердых стенках;
– тепловые условия – заданный тепловой поток на верхней прозрачной границе (моделирующей поглощение солнечной радиации) и теплоизоляцию на остальных стенках, либо заданный коэффициент теплоотдачи при наличии внешнего охлаждения.
Такой подход позволяет корректно описать взаимосвязь между оптическим поглощением, гидродинамикой и теплопередачей в НКПП с учетом реологических особенностей наножидкости, что согласуется с методологиями, применяемыми в современных исследованиях подобных систем [9; 10].
Результаты исследования и их обсуждение
Рассмотрим прямоугольную область 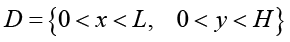 , где L и H – длина и высота солнечного коллектора (рис. 1), причем
, где L и H – длина и высота солнечного коллектора (рис. 1), причем  .
.
Рассмотрим задачу определения скорости V = (v,u) рабочей жидкости в тонком коллекторе. Считаем, что движение жидкости в коллекторе установилось, скорость течения не зависит от времени. Для построения математической модели используем стационарное уравнение Навье – Стокса и уравнение несжимаемости, которые запишем в двумерной покомпонентной форме для составляющих вектора скорости в декартовой системе координат x, y.
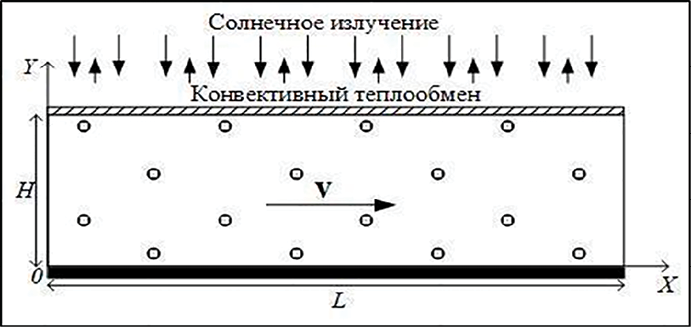
Рис. 1. Упрощенная схема солнечного коллектора Примечание: составлен авторами на основе источника [2]
Уравнение движения в проекции на ось Ох:
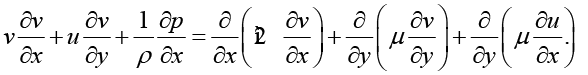 (1)
(1)
Уравнение движения в проекции на ось Оy:
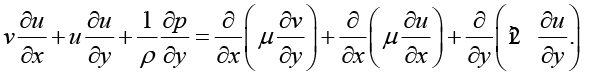 (2)
(2)
Уравнения несжимаемости:
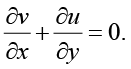 (3)
(3)
Здесь p – давление, ρ – плотность жидкости, μ – кинематическая вязкость.
Граничные условия в соответствии с физической постановкой зададим следующим образом:
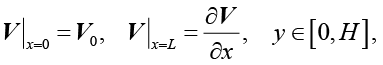 (4)
(4)
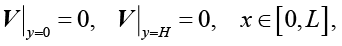 (5)
(5)
где L и H – соответственно длина и ширина НКПП, 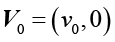 ,
, 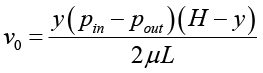 – аналитическое выражение для продольной скорости жидкости в солнечном коллекторе прямого поглощения.
– аналитическое выражение для продольной скорости жидкости в солнечном коллекторе прямого поглощения.
Для однозначного определения давления используется соотношение
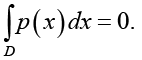 (6)
(6)
Соотношения (1)–(6) позволяют записать задачу, описывающую процессы теплопереноса в солнечном коллекторе прямого поглощения, в виде следующей краевой задачи:
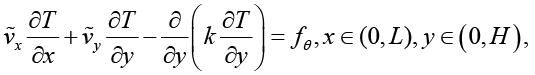 (7)
(7)
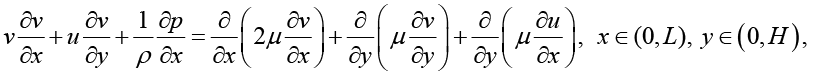 (8)
(8)
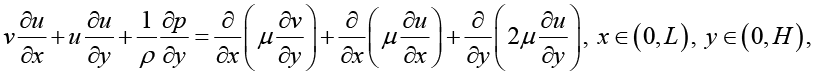 (9)
(9)
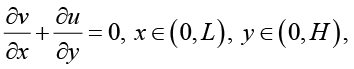 (10)
(10)
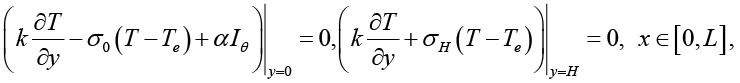 (11)
(11)
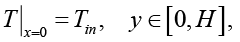 (12)
(12)
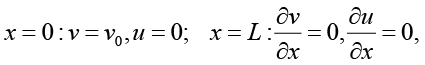 (13)
(13)
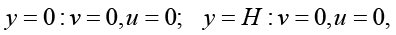 (14)
(14)
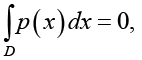 (15)
(15)
где ṽx = cvv, ṽy = cvu; Iθ и fθ задаются выражениями, представленными в работе [11]; Te – температура окружающей среды; σ0, σH – коэффициенты теплоотдачи на нижней и на верхней границах коллектора соответственно.
Построим для задачи (7)–(15) конечно-разностную схему.
Нанесем на область Ω = {0 ≤ x ≤ L, 0 ≤ y ≤ H} равномерную сетку
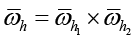 ,
, 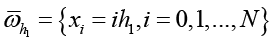 ,
, 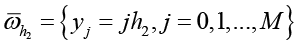 ;
;
h1 = L/N, h2 = H/M – шаги сетки 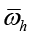 по пространственным переменным x и y; N, M – натуральные числа; h = {h1,h2}.
по пространственным переменным x и y; N, M – натуральные числа; h = {h1,h2}.
Для упрощения записи будем использовать следующие обозначения для сеточных функций и выражений, содержащих конечно-разностные производные
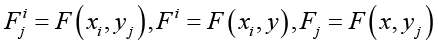 ,
,
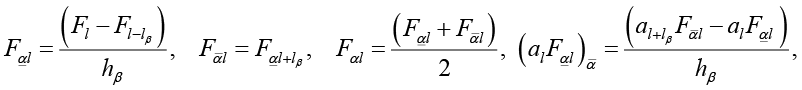
где l = {i, j}, α = x,y, β = 1,2, l1 = {1,0}, l2 = {0,1}.
Записывая уравнения баланса для элементарных ячеек сеточной области, получаем для задачи (7)–(15) симметричную консервативную конечно-разностную схему, которую с учетом введенных обозначений можно записать в виде системы уравнений
для 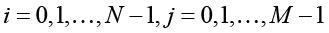 :
:
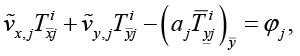 (16)
(16)
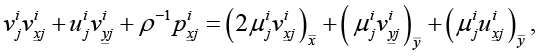 (17)
(17)
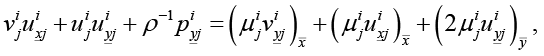 (18)
(18)
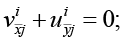 (19)
(19)
для 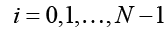 :
:
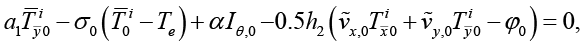 (20)
(20)
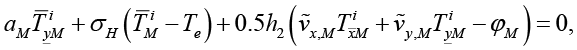 (21)
(21)
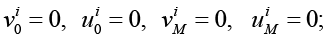 (22)
(22)
для 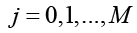 :
:
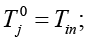 (23)
(23)
и для 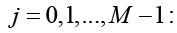
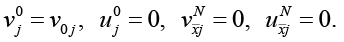
Таблица 1
Теплофизические свойства этиленгликоля
|
Температура T, ºC |
Плотность ρ, кг/м3 |
Удельная теплоемкость сv , Дж / (кг∙К) |
Кинематическая вязкость v, (м2/с)∙106 |
Теплопроводность k, Вт/(м∙К) |
Число Прандтля Pr |
|
0 |
1130,1 |
2 294 |
26,5 |
0,242 |
283,884 |
|
20 |
1116,1 |
2 382 |
14,4 |
0,249 |
153,747 |
|
40 |
1100,8 |
2 474 |
8,5 |
0,256 |
90,425 |
|
60 |
1087,1 |
2 562 |
5,2 |
0,260 |
55,703 |
|
80 |
1077,0 |
2 650 |
3,4 |
0,262 |
37,037 |
|
100 |
1057,9 |
2 742 |
2,5 |
0,263 |
27,574 |
Примечание: составлена авторами на основе источника [14, с. 7–433].
В численных экспериментах в качестве базовой жидкости выбран этиленгликоль. Такой выбор обусловлен рядом нужных термофизических характеристик данного вещества, подтвержденных справочными данными и результатами предшествующих исследований. В частности, анализ показывает, что теплофизические свойства этиленгликоля (включая плотность, динамическую вязкость, теплопроводность и теплоемкость) демонстрируют выраженную зависимость от температуры [7 с. 253–281; 11]. Достаточно сильная температурная чувствительность делает этиленгликоль особенно подходящим веществом для численного моделирования процессов тепломассопереноса, позволяя выявить и количественно оценить влияние нестационарных и нелинейных эффектов на гидродинамическое и тепловое поведение системы [12; 13]. Поэтому использование этиленгликоля в качестве модельной жидкости повышает информативность и репрезентативность проводимых вычислительных экспериментов.
Используем данные об основных теплофизических свойствах этиленгликоля, необходимые для расчетов, размещенные в справочнике [14, с. 7–433] (табл. 1).
При проведении численных расчетов применены приближенные аналитические зависимости, полученные на основе данных табл. 1. Для аппроксимации экспериментальных значений применялись метод наименьших квадратов для различных интерполяционных функций, а также методы регрессионного и интерполяционного анализа. Данные подходы позволили построить аппроксимирующие выражения для определения таких теплофизических параметров этиленгликоля, как динамическая вязкость, плотность, удельная теплоемкость и теплопроводность:
μ = v∙ρ, (25)
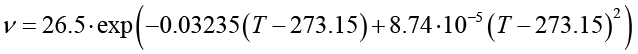 , (26)
, (26)
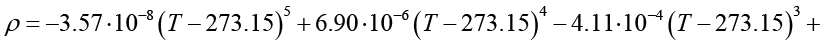
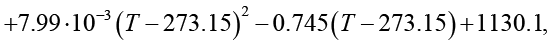 (27)
(27)
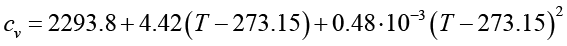 , (28)
, (28)
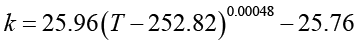 , (29)
, (29)
Pr = cv μ / k. (30)
Полученные зависимости обеспечивают погрешность не более 0,4 % относительно данных, приведенных в табл. 1. При выполнении расчетов с использованием выражений (25)–(30) температура T должна быть представлена в градусах Кельвина. Перевод значений температуры из термодинамической шкалы Кельвина в шкалу Цельсия осуществляется в соответствии с соотношением, учитывающим разность, равную 273,15 градуса.
Исследование физических процессов, протекающих внутри НКПП, проводится с использованием метода расщепления по физическим процессам [15, с. 85–89]. Численное исследование задач для уравнений Навье – Стокса и построение алгоритмов решения на основе расщепления по физическим процессам отражает природу течений и широко используется в современных исследованиях [16; 17].
В рамках настоящего исследования применен метод операторного расщепления для решения задачи тепломассопереноса, заключающийся в декомпозиции исходной системы уравнений на два последовательных этапа – термодинамический и гидродинамический. Расщепление осуществляется непосредственно на уровне дифференциальных уравнений, записанных в терминах исходных физических переменных, без перехода к вспомогательным или обобщенным величинам.
На термодинамическом этапе решается уравнение энергии с целью определения пространственного распределения температурного поля при заданном поле скоростей. Гидродинамический этап включает моделирование движения рабочей жидкости, в ходе которого рассчитывается поле скоростей под действием градиентов давления и температурных неоднородностей, обуславливающих конвективные потоки.
Решение реализуется в рамках итерационной процедуры, на каждом шаге которой последовательно вычисляются характеристики обоих этапов. Итерационный процесс продолжается до достижения заданной точности сходимости между последовательными приближениями температурного поля:
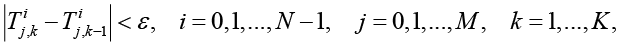 (31)
(31)
где 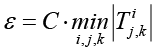 , C = 10–6, k – номер итерации. Данное условие обеспечивает согласованность полученных результатов с исходной постановкой задачи.
, C = 10–6, k – номер итерации. Данное условие обеспечивает согласованность полученных результатов с исходной постановкой задачи.
Общая схема решения задачи включает следующие этапы:
1) расчет температурного поля с учетом начальных условий;
2) вычисление значений динамической вязкости в каждой точке расчетной области проводится с использованием температурных зависимостей и аналитических выражений (25)–(30);
3) расчет поля скоростей путем решения системы уравнений (8)–(10), (13)–(15) с учетом полученного распределения динамической вязкости;
4) решение задачи теплопроводности (7), (11), (12), учитывающей как поперечную, так и продольные компоненты вектора скорости течения рабочей жидкости.
Описанные этапы 1–4 повторяются в рамках итерационного процесса до достижения заданной точности.
Для проверки работоспособности математической модели (7)–(15) проведем численный эксперимент со следующими исходными данными:
примем высоту солнечного коллектора H и длину L равными 0,02 м и 1 м соответственно;
Tin = 35ºC – входная температура наножидкости в солнечном коллекторе;
Te = 25ºC – температура на верхней стенке;
τ = 0.9 – коэффициент пропускания верхней границы НКПП;
σ0 = σH ∙ 10–2 Вт/(м2∙К) – коэффициент теплоотдачи на нижней границе НКПП;
σH = 6.43 Вт/(м2∙К) – коэффициент теплоотдачи па верхней границе НКПП, взятый из [2];
GT – коэффициент пропорциональности, соответствующий интенсивности приходящего солнечного излучения на верхнюю границу коллектора равной 1000 Вт/м2;
α = 0 – коэффициент, позволяющий учитывать эффекты отражения и поглощения светового потока на нижней границе, принимающий значения 0 и 1.
Таблица 2
Результаты сходимости итерационного процесса
|
k |
|
ε |
Достижение устойчивого состояния |
|
0 |
– |
– |
– |
|
1 |
3,0086552E+00 |
35E-06 |
нет |
|
2 |
6,6066468E-02 |
35E-06 |
нет |
|
3 |
2,3994639E-03 |
35E-06 |
нет |
|
4 |
6,6416215E-05 |
35E-06 |
нет |
|
5 |
1,9965515E-06 |
35E-06 |
да |
Примечание: составлена авторами на основе полученных данных в ходе исследования
|
|
|
|
а) |
б) |
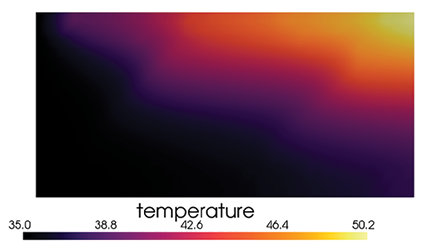
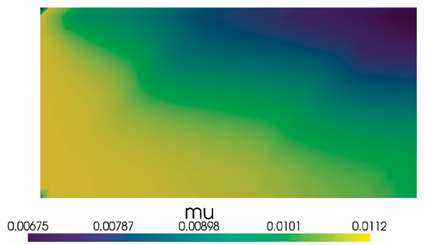
Рис. 2. Результаты численного эксперимента для наножидкости: а) распределение температуры по сечению коллектора; б) распределение динамической вязкости Примечание: составлен авторами по результатам данного исследования
|
|
|
|
а) |
|
|
|
|
|
б) |
в) |
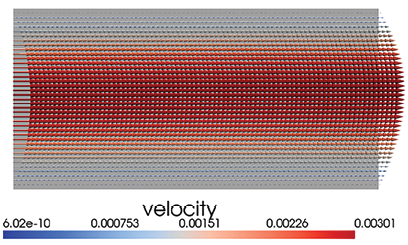
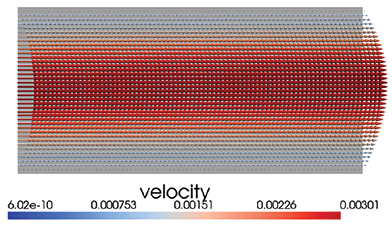
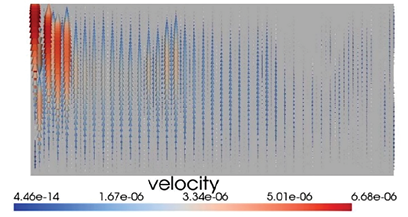
Рис. 3. Результаты моделирования потока наножидкости внутри НКПП: а) общий поток скорости; б) компонента скорости v; в) компонента скорости u Примечание: составлен авторами по результатам данного исследования
В качестве материала наночастиц рассмотрим частицы алюминия. Теплофизические характеристики материала наночастиц выбраны из справочной литературы по оптическим константам и теплофизическим свойствам различных материалов [14, с. 7–433], а для базовой жидкости (этиленгликоля) с целью получения наиболее точных численных результатов будем использовать выражения (25)–(30).
Итерационный процесс с использованием критерия (31), запущенный в рамках данного численного эксперимента, сошелся за 5 итераций. В табл. 2 представлены его результаты.
На рис. 2 для наножидкости на основе дистиллированной воды и диспергированных в ней наночастиц алюминия представлены графики распределения температуры (рис. 2, а), а также распределение динамической вязкости (рис. 2, б) по сечению коллектора для последней итерации.
На рис. 3 представлены результаты численного решения краевой задачи, отражающие пространственное распределение векторного поля скорости в расчетной области; а) – общий поток скорости; б) – компонента скорости v; в) – компонента скорости u. Каждый график сопровождается цветовой шкалой, соответствующей значению гидродинамической переменной в физических или безразмерных единицах, что обеспечивает визуальную интерпретацию структуры течения и позволяет идентифицировать зоны с различной интенсивностью конвективного переноса.
Анализ безразмерных параметров, определяющих динамику и теплообмен в системе, выполнен на основе значений числа Рейнольдса Re = 150,64, числа Прандтля Pr = 190,51, числа Рэлея Ra = 1,27.
Анализ результатов численных экспериментов позволяет сделать следующие выводы:
1. В системе существует температурная зависимость динамической вязкости, что заметно сказывается на профиле скорости. Наблюдается увеличение локальных скоростей в областях с повышенной температурой, где вязкость снижается (рис. 3). Данный эффект является следствием реологической чувствительности наножидкости и подтверждает необходимость учета немонотонных физических свойств даже в отсутствие объемных сил.
2. Распределение поля скорости (рис. 3) демонстрирует явную связь с температурным полем, обусловленную зависимостью вязкости от температуры. Это свидетельствует о том, что термореологическое взаимодействие играет ключевую роль в формировании гидродинамической структуры потока даже при отсутствии плавучести.
Дальнейшее развитие исследований в данной области направлено на применение наножидкостей, содержащих смесь наночастиц различных веществ, что позволит получить дополнительный эффект за счет комбинированного влияния различных типов наночастиц на теплопроводность, вязкость и стабильность суспензии. Такой подход открывает возможности для тонкой настройки термофизических свойств наножидкости под конкретные условия эксплуатации, включая управление локальными градиентами скорости и температуры в сложных геометриях.
Заключение
В работе построена математическая модель, позволившая решить задачу расчета параметров тепломассопереноса в наножидкостном солнечном коллекторе прямого поглощения при установившемся течении. Модель включает уравнения сохранения массы, импульса и энергии с учетом температурной зависимости динамической вязкости рабочей среды, а также спектрального поглощения солнечного излучения на основе закона Бугера – Ламберта – Бера. В качестве теплоносителя использована наножидкость, состоящая из этиленгликоля с наночастицами алюминия, что обеспечило выраженную термозависимость ее реологических свойств.
Результаты численных экспериментов показали, что учет температурной зависимости вязкости существенно влияет на гидродинамическую структуру потока: в зонах локального нагрева наблюдается снижение вязкости и, как следствие, увеличение скорости течения. Установлена тесная связь между температурным и скоростным полями, подтверждающая значимость термореологического взаимодействия даже в условиях отсутствия гравитационной конвекции. Это обуславливает необходимость включения немонотонных теплофизических свойств в модели наножидкостных солнечных коллекторов для достижения высокой точности прогнозирования их тепловой эффективности.
Полученные результаты создают основу для дальнейших исследований, включая использование гибридных наножидкостей с комбинированным составом наночастиц, что может позволить эффективно управлять оптическими и реологическими характеристиками теплоносителя с целью повышения общей производительности систем солнечной энергетики.