Введение
Заочная форма обучения сегодня является востребованной среди студентов педагогических направлений. Это связано с тем, что имеется значительный дефицит учителей на рынке труда и многие школы готовы принять на работу студентов. Большинство студентов заочной формы обучения уже с первого курса работают учителями в школе на полную ставку, имеют классное руководство и полностью включены в жизнь школы. Они на практике сталкиваются с различными проблемами и ситуациями, хотя теоретически не готовы к ним, так как ими еще не изучены ни педагогика, ни психология, ни методика преподавания предмета. При этом не будем забывать, что, в отличие от студентов очной формы обучения, они изучают данные дисциплины в большей степени самостоятельно.
Будущим учителям математики необходимо не только понимать, как учить школьников математике в соответствии с программой школьного курса и возрастными особенностями, но и быть готовыми к подготовке их к ОГЭ и ЕГЭ, к олимпиадам. При этом они сами должны владеть на высоком уровне предметными математическими знаниями, а также методикой организации урочной, внеурочной, исследовательской и проектной деятельностей. Следовательно, нужно учитывать учебно-методические аспекты обучения студентов-заочников в вузе [1; 2].
Работая в школе и получая образование заочно, студенты сталкиваются с множеством проблем, которые можно решить как при правильной организации обучения со стороны вуза, так и путем самоорганизации и самообучения. Современная система образования позволяет предоставлять студентам разные формы обучения: онлайн, дистанционную, смешанную. Студент всегда остается на связи с преподавателем, что позволяет решать многие учебные задачи.
Выявление проблем и трудностей студентов-заочников в рамках изучения методики обучения математике позволяет организовать процесс изучения дисциплины таким образом, чтобы студенты получали необходимые теоретические знания, были готовы к решению различных методических ситуаций в своей практической деятельности, получали ответы на вопросы и методическую поддержку со стороны преподавателей вуза, могли общаться между собой, участвовать в научных семинарах и обучаться на опыте других учителей, включаться в исследовательскую деятельность и даже повышать квалификацию и получать дополнительные умения и навыки, важные для педагога. Это позволяет сделать применение инновационных подходов в обучении [3; 4].
Опыт работы со студентами-заочниками и проведенные опросы, беседы и анкетирования позволили выявить ряд особенностей методической подготовки, которые влияют на процесс их обучения, а их учет при разработке программы, пособий и заданий – сделать этот процесс более эффективным и качественным.
Цель исследования – выявление особенностей методической подготовки будущих учителей математики заочной формы обучения для организации процесса обучения в вузе по дисциплине «Методика обучения математике».
Материалы и методы исследования
Методическая подготовка будущих учителей математики заочной формы обучения в ПсковГУ включает в себя изучение дисциплин «Методика обучения математике» (общая и частная), «Современные технологии обучения математике». Данные дисциплины предполагают теоретическую и практическую подготовку. Практические навыки отрабатываются при выполнении методических заданий на аудиторных занятиях и самостоятельно, а также в ходе учебной, методической и педагогической практик [5–7].
Однако следует отметить, что эта подготовка отличается от той, которую проходят студенты очной формы обучения, а связано это в первую очередь с тем, что многие студенты-заочники являются действующими учителями-предметниками (хотя есть и те, кто в школе не работает), что влияет и на теоретическую подготовку студентов, и на возможность посещения занятий, и на выполнение практических заданий.
Поэтому для организации методической подготовки будущих учителей математики, обучающихся заочно в Псковском государственном университете, было проведено исследование в течение 2020–2023 гг., которое было направлено на выявление особенностей обучения студентов методике обучения математике. Для исследования применялись такие методы, как беседа, анкетирование и анализ опыта работы преподавателя. Выявленные особенности позволили выстроить процесс обучения методике обучения математике более качественно и эффективно.
Результаты исследования и их обсуждение
Наличие опыта работы в школе накладывает отпечаток на изучение методики математики, так как работающий учитель не всегда согласен с теоретическими положениями, он сталкивается с тем, что теория не всегда работает на практике, имеются вопросы: «А что делать, если я делаю так… а они не слушают/не понимают…?»; «Как применять знания, если в классе ученики с разной математической подготовкой?» и др. И это первая особенность – наличие опыта работы в школе, которая требует иной организации процесса теоретической подготовки студентов заочной формы обучения.
Однако нельзя забывать, что есть и студенты, которые не работают в школе и опыта не имеют, а следовательно, подход к их теоретической подготовке будет иной. Перед преподавателем встает задача – совместить обучение студентов с разным опытом и знаниями и при этом в сжатые сроки сессии.
Лабораторная работа по теме «Методика работы с сюжетной задачей» [11, с. 49]
|
№ |
Задание |
Требования |
|
1. |
Приведите примеры сюжетных задач, используя школьные учебники математики: 1) на движение; 2) на совместную работу; 3) на сплавы и смеси; 4) с экономическим содержанием; 5) др. |
По задачи каждого вида |
|
2. |
2.1. Приведите примеры текстовых задач, которые нельзя отнести к сюжетным. Объясните, почему нельзя. 2.2. Разъясните понятие «межпредметная задача» и приведите примеры таких задач из школьных учебников |
По 2–3 задачи в каждом пункте |
|
3. |
3.1. Решите задачу арифметическим способом. Задача: Из двух поселков, находящихся на расстоянии 66 км друг от друга, одновременно навстречу друг другу выехали 2 велосипедиста и встретились через 2 ч. Один ехал со скоростью 15 км/ч. Найдите скорость второго велосипедиста. 3.2. Сформулируйте последовательность вопросов учителя к учащимся при работе над задачей. 3.3. Можно ли решить эту задачу алгебраическим способом? Если да, то решите и опишите этапы решение |
Пояснение: арифметический способ решения – по действиям; алгебраический – введение переменных, составление уравнений |
|
4. |
Сравните арифметический и алгебраический способы решения задачи из пункта № 3. Выберите наиболее эффективный для учащихся 5 класса, 6 класса, 7–9 классов, выбор обоснуйте |
Оформить в виде таблицы |
|
5. |
5.1. Оформите решение задачи алгебраическим способом, обозначая за неизвестную каждый раз разную величину. Задача: Расстояние АВ, равное 110 км, турист прошел за 3 дня. За второй день пути он прошел на 5 км меньше, чем за первый, а за третий день – 3/7 расстояния, пройденного за два первых дня. Сколько километров проходит турист за каждый день пути? 5.2. Выполните графическую иллюстрацию условия задачи. 5.3. Представьте поиск решения задачи в виде таблицы |
5.1. Должно получиться 3 варианта решения (3 математические модели) |
|
6. |
6.1. На основе проделанной работы разработайте фрагмент плана-конспекта собственного урока по работе с задачей №___. 6.2. Напишите рекомендации для учителя по работе на уроке математики с такой задачей: как мотивировать ее решение, как провести анализ условия и т.д. |
У каждого студента своя задача из списка (Приложение 3) |
Поэтому был выбран следующий путь: до начала сессии (когда будет прочитан курс лекций по предмету) создается дистанционный курс, где размещается основной теоретический материал по разделу дисциплины, который будет изучаться в семестре. Студенты могут ознакомиться с ним, подготовить заранее вопросы, обозначить непонятные для них моменты, определить, где стоит преподавателю более подробно остановиться для изучения в аудитории. Это позволяет более эффективно изучить теоретический материал на сессии, применяя современные формы обучения, такие как «перевернутые» учебные ресурсы и информационные технологии [8–10].
Практическая подготовка начинается только на сессии, студенты выполняют задания для отработки теоретических знаний. При изучении общей методики это могут быть задания по написанию фрагментов уроков по изучению нового понятия, работе с теоремой или решению задачи. А для самостоятельной работы студентам могут быть предложены комплексы заданий, которые направлены на формирование методических знаний и отработку методических умений по целому блоку или теме. Например, в пособии «Практикум по общей методике обучения математике» [11] для студентов заочной формы обучения предлагаются лабораторные работы по основным темам. В таблице представлена одна из таких лабораторных работ, где задания ранжируются по уровню сложности образовательных учебных целей (на основе таксономии Блума) и формируют основные умения по теме «Методика работы с сюжетной задачей».
В приложении 3 представлен пример списка задач [11, с. 51], с которыми работают студенты. Работа выполняется каждым студентом индивидуально, на сессии или на онлайн-консультации преподаватель комментирует, как выполняется каждый пункт лабораторной работы, отвечает на вопросы студентов. Математические задачи в пунктах 3 и 5 у каждого студента могут быть разные, что повысит уровень самостоятельности студентов. Ответы на задания в каждом пункте студенты записывают подробно, с обоснованиями и объяснениями. В случае затруднений при выполнении работы могут быть проведены консультации (групповые или индивидуальные) или студенты могут задавать вопросы в чате дистанционного курса. Работа должна быть выполнена к определенному сроку и загружена в дистанционный курс до начала сессии. Она принимается для оценивания, только если выполнены все задания в соответствии с требованиями, и может быть возвращена на доработку. Выполнение таких лабораторных работ считается обязательным, может являться как частью рейтинга, так и допуском к экзамену.
Также в ходе аудиторной работы на сессии студентам предлагается описать те методические ситуации, которые возникали в их педагогической деятельности, определить математические темы школьного курса, которые вызывают сложности при изучении школьниками и преподавании. Для этого разрабатывается опросник, где студенты записывают ответы на ряд вопросов. Также эта работа может быть организована как групповая беседа, если число студентов в группе невелико и есть возможность выслушать каждого. Это позволяет вузовскому преподавателю построить систему изучения следующего раздела методики таким образом, чтобы подготовить для изучения важный теоретический материал и разработать практические задания. При этом лекционный материал по следующему разделу также заранее размещается в дистанционном курсе.
При изучении частной методики изучения математики обязательно проводится работа с методическими ситуациями, которые являются частью государственного экзамена. На занятии студентам предлагается методическая ситуация, которая разработана преподавателем на основе материалов опроса студентов в прошлую сессию, она подробно разбирается, выполняются задания к ситуации. Затем студентам предлагается самостоятельно составить методическую ситуацию (или же преподаватель дает готовые ситуации), обменяться ими и выполнить задания к ним. Такая работа помогает лучше разобраться в самом понятии «методическая ситуация», понять проблему, научиться формулировать методическую проблему в рамках учебного предмета и искать ее решения. Приведем пример методической ситуации и заданий к ней.
Ситуация: при изучении темы «Квадратичная функция» ученик, выполняя упражнения на построение графиков функций, допускает ошибки в построении, так как строит график «по точкам», подставляя целые числа.
Вопросы и задания:
1. Прокомментируйте ситуацию.
2. Проведите логико-дидактический анализ темы, которая направлена на формирование умений решать задание, описанное в ситуации. Выделите основные знания и умения, необходимые учащимся для того, чтобы предупредить возникновение такой ситуации.
3. Представьте разработку индивидуального занятия с одним учеником, направленного на коррекцию описанной ситуации.
Раздел «Современные технологии обучения математике» изучается таким образом, чтобы студенты не только узнали, какие технологии можно применять на современном этапе обучения школьников математике, но и поделились имеющимся опытом друг с другом и на опыте разработали продукты, которые они смогут применить для эффективного обучения предмету. Например, многие активно применяют на уроках математики динамическую математическую программу GeoGebra, но не знакомы с российской программой динамической математики Математический конструктор (https://obr.1c.ru/mathkit/), который имеет много возможностей для организации уроков математики по всем разделам. Студенты могут в компьютерном классе сами создавать интерактивные задания, разрабатывать свои дистанционные курсы, создавать проверочные работы, кроссворды и многое другое. Также для получения зачета по дисциплине студенты получают индивидуальное задание по разработке онлайн-уроков, курсов или других материалов по математике с применением современных технологий обучения, которое нужно выполнить и защитить на зачетном занятии, представив его группе.
Второй особенностью, которая влияет на качество методической подготовки, является не постоянное изучение дисциплины, а в сжатые сроки на сессии (а это две-три недели). Это связано и с тем, что многие работают и не имеют возможности заниматься и выполнять задания в течение всего семестра, а также не имеют навыков самоорганизации. Так дело обстоит и с изучением теоретического материала – если имеется список литературы по предмету, искать информацию в разных источниках неудобно и долго. Поэтому для студентов заочной формы обучения написаны учебно-методические пособия по методике обучения математике, которые в электронной форме размещаются в дистанционном курсе. В пособиях представлен весь теоретический материал, который входит в экзаменационные билеты по дисциплине. Также пособия содержат задания для практических занятий, индивидуальные задания. Например, в пособии «Практикум по частной методике обучения математике» в разделе «Линия уравнений и неравенств» [12, с. 32–33] предлагаются следующие задания:
Задание 1. На основе анализа школьных учебников заполните таблицу
|
Вид уравнения |
Способы и методы решения |
Алгоритм решения |
Особенности методики |
|
Линейные уравнения |
Алгебраический |
1) привести подобные слагаемые; 2) привести к виду 3) |
Отработать умение преобразовывать уравнение к равносильному ему. Обратить внимание на перенос слагаемых из одной части в другую (меняем знак) |
|
Графический |
1) ввести функции, которые являются левой и правой частями уравнения; 2) построить графики этих функций в одной системе координат; 3) найти точки пересечения этих графиков; …. |
Нужно правильно (рационально) вводить функции. Нужно точно строить графики функций. Знать, что является графиком функции |
|
|
… |
|||
|
Квадратные уравнения |
|||
|
… |
Задание 2. Продумайте возможности систематизации знаний при изучении темы «Тригонометрические уравнения». Предложите способы систематизации и подберите задания к одному из предложенных способов.
Задание 3. Укажите ошибки, которые чаще всего допускают обучающиеся при решении следующих уравнений:
1) 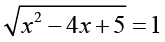 ;
;
2) 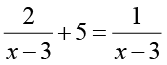 ;
;
3) 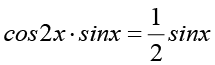 .
.
Предложите способы работы с учащимися, чтобы предотвратить эти ошибки.
Задание 4. Разработайте методику изучения следующих тем: «Логарифмические неравенства», «Решение простейших тригонометрических неравенств». Какие трудности могут возникать при изучении данных тем? Предложите методику работы с учениками, которые испытывают затруднения при решении данных видов неравенств.
Такие задания студенты могут выполнять самостоятельно и загружать ответы в дистанционный курс. Преподаватель проверяет их выполнение, может отправлять на доработку. В случае необходимости проводится онлайн-консультация, где разбираются ошибки, преподаватель отвечает на вопросы, объясняет требования по выполнению заданий. Такая организация обучения студентов позволяет им чувствовать себя включенными в процесс обучения в ходе всего семестра и выполнять задания осознанно.
Третья особенность – это невозможность приехать на сессию (по разным причинам) у некоторых студентов, которые работают. Эта проблема также решаема, если студент переводится на дистанционное обучение, для него организуется обучение таким образом, что он может онлайн подключаться к лекциям, задавать вопросы, участвовать в обсуждениях. Или же он может самостоятельно изучить теоретический материал в дистанционном курсе, задать вопросы в чате преподавателю, выполнить практические задания и загрузить их для проверки в дистанционном курсе. При необходимости преподаватель может назначить индивидуальную консультацию или провести беседу по выполненным заданиям онлайн в удобное для всех время. Это позволяет не отставать от однокурсников и не иметь долгов по дисциплине. При этом экзамен или зачет также может быть проведен онлайн с соблюдением всех требований или с учетом балльно-рейтинговой системы [13; 14], что позволяет выбрать наиболее оптимальный вариант проверки знаний студентов [15].
Заключение
Заочная форма обучения в современных условиях позволяет студентам работать учителями в школе и одновременно получать образование. Такая необходимость продиктована запросами системы образования и нехваткой учителей математики в школах как Псковской области, так и других регионов. Поэтому вузы должны подстраиваться под эти запросы, создавая возможность получать качественное образование в доступной форме.
Проведенное исследование в рамках ПсковГУ позволило выявить особенности методической подготовки студентов-математиков при заочной форме обучения, на которые стоит обратить особое внимание. Опыт обучения таких студентов позволил найти эффективные пути изучения методики обучения математики с учетом выделенных особенностей и построить процесс обучения таким образом, чтобы студенты как изучали на высоком уровне ее теоретическую часть, так и получали необходимые практические умения. Были разработаны дистанционные курсы с учебными материалами, которые позволяют студентам изучать дисциплину в удобное для них время и в доступной форме; созданы пособия и системы заданий для отработки необходимых методических умений; организован процесс аттестации в индивидуальной форме.




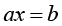 ;
;