Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 1,172

Введение

Рак молочной железы (РМЖ) – одно из самых распространенных онкологических заболеваний у женщин. Согласно данным Всемирной организации здравоохранения, на него приходится каждый шестой случай заболевания раком среди женщин. В 2022 г. в мире было выявлено 2,3 млн новых случаев. В России ежегодно РМЖ обнаруживают у 70 тыс. женщин и более 20 тыс. умирают. Злокачественные новообразования молочной железы остаются огромной медико-социальной проблемой, нанося колоссальный ущерб на государственном, региональном и индивидуальном уровнях [1].

На сегодняшний день классификация РМЖ основана на пяти биологических подтипах (биотипов) опухоли, которые различаются по прогнозу, агрессивности и чувствительности к различным видам лекарственной терапии: 1 – люминальный A; 2 – люминальный B; 3 – люминальный В HER2+; 4 – нелюминальный HER2+; 5 – базальноподобный TNBC [2]. Своевременное установление подтипа РМЖ позволяет подобрать индивидуальную схему лечения заболевания и улучшает выживаемость и прогноз [3]. В настоящее время биотип опухоли определяют с помощью иммуногистохимического анализа, относящегося к инвазивным методам исследования [4]. Очевидно, что актуальной проблемой является переход к неинвазивному установлению биотипа РМЖ, основанному на использовании адекватных математических моделей, учитывающих основные особенности данных. Сложность решения этой проблемы лучевой диагностики рака молочной железы требует комплексного исследования с применением современной технологии математического моделирования и вычислительного эксперимента.

К основным диагностическим методам визуализации относят рентгеновскую проекционную маммографию и ультразвуковое исследование. В ряде публикаций [2–6] отмечается определенный прогресс в использовании данных неинвазивных инструментов диагностики и оценки биологии опухоли. Одним из развивающихся направлений в неинвазивной диагностике является использование энтропийного анализа медицинских изображений. Публикуется большое количество работ, например [7–9], можно отметить определенный успех на стадии обнаружения отдельных заболеваний, включая и онкологию.

Однако пока отсутствуют обоснованные количественные критерии установления биотипа РМЖ на ранней стадии заболевания. Это можно объяснить тем, что данная проблема является более сложной по сравнению с обнаружением по изображениям РМЖ. По нашему мнению, ее эффективное решение требует системного подхода к математическому моделированию [10–12].

Цель исследования – комплексное исследование проблемы лучевой диагностики рака молочной железы на основе рентгенологических и ультразвуковых характеристик опухолей с применением современной технологии математического моделирования и вычислительного эксперимента.

Материалы и методы исследования

Из пациентов, проходивших обследование в Свердловском областном онкологическом диспансере с 2020 г., была сформирована выборка результатов рентгенологического и ультразвукового обследований для 365 пациенток возраста от 31 до 86 лет. Диагностические показатели описаны во многих публикациях [2; 13; 14, с. 49–79]. Они приведены в табл. 1. Для определения биотипов РМЖ было проведено комплексное гистологическое и иммуногистохимическое исследование всех пациенток. В результате в выборке оказались больные из всех пяти биотипов, в которых имеется 107, 177, 27, 21, 33 наблюдения соответственно.

Исследование включает две задачи. Во-первых, исследуем возможность по векторам рентгенологических 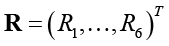и ультразвуковых 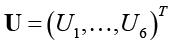показателей корректно классифицировать больных в соответствии с установленными биотипами. Многие авторы отмечают влияние возраста T на особенности заболевания, поэтому его также будем учитывать в анализе.

Во-вторых, попробуем найти существенные различия между биотипами на основе анализа рентгенологических и ультразвуковых показателей пяти кластеров (групп) пациенток.

Одним из наиболее распространенных методов классификации данных по обучающей выборке является линейный дискриминантный анализ [15, с. 10–17]. Он основан на возможности разделения совокупности данных на L кластеров с помощью гиперплоскостей, на основе обучающей выборки данных. Здесь объединяем все показатели в одно множество (вектор):

.

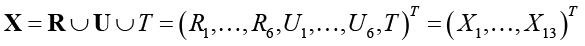Таблица 1

Система рентгенологических и ультразвуковых показателей

Рассмотрим его использование на примере двух кластеров [16, с. 509–516]. В этом случае имеем уравнение разделяющей гиперплоскости

,

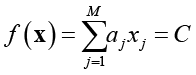где f(x) – дискриминантная функция, M – число переменных (анализируемых показателей), C – константа дискриминации, 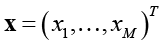. Если f(xº) > C, то наблюдение xº относим к первому кластеру, если f(xº) < C, то ко второму.

Вектор коэффициентов 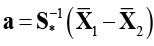, где 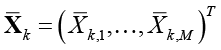– вектор средних значений показателей k-го кластера; 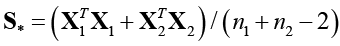– объединенная ковариационная матрица; Xk – матрица значений показателей k-го кластера; nk – число наблюдений в k-м кластер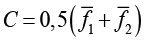е; , где 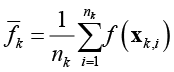; k = 1,2.

Модели на основе дискриминантного анализа и других методов классификации не учитывают многомерную корреляцию анализируемых показателей. Для учета корреляций нужно рассматривать не отдельные наблюдения, а в целом биотипы РМЖ. Одним из подходов, учитывающих такие корреляции, является векторное энтропийное моделирование [17, с. 94–99]. Отметим несколько публикаций, в которых оно было применено для различных задач медицинской диагностики [18–20]. Этот подход основан на векторном представлении дифференциальной энтропии, введенной в [21] как энтропия непрерывного распределения многомерной непрерывной случайной величины.

Дифференциальная энтропия (далее – энтропия) M-мерного случайного вектора 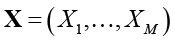равна [17, с. 94]:

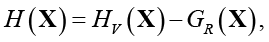(1)

где

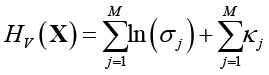– энтропийная «мера хаотичности»,

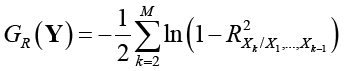– энтропийная «мера самоорганизации», σj – среднеквадратическое отклонение случайной величины Yj, 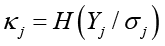– энтропийный показатель типа закона распределения случайной величины Yj, 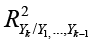– индексы детерминации регрессионных зависимостей.

Согласно (1): 1) если между компонентами случайного вектора X отсутствует строгая функциональная связь, но хотя бы одна компонента коррелирована Xj хотя бы с одной компонентой Xk (j ≠ k), то 0 < GR(X) < ∞; 2) если хотя бы одна компонента Xj строго функционально связана хотя бы с одной компонентой Xk (j ≠ k), то GR(X) = ∞; 3) если все компоненты случайного вектора X взаимно независимы, то GR(X) = 0; 4) чем теснее корреляционная связь между компонентами случайного вектора X, тем больше значение GR(X). В частном случае, когда X – гауссов случайный вектор, имеем

,

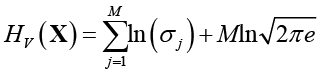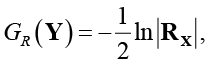(2)

где Rx – корреляционная матрица случайного вектора X.

Энтропия (1) состоит из двух составляющих. Первое слагаемое HV(X) определяет предельную энтропию, соответствующую полной независимости показателей X, и характеризует рассмотрение системы (РМЖ) как состоящего из частей (аддитивность). Второе слагаемое GR(X) отражает степень взаимосвязей между показателями, характеризуя свойства системы как целого (целостность). Поскольку HV(X) и GR(X) характеризуют разные стороны поведения заболевания как системы, то будем рассматривать энтропию (1) в векторной форме в виде двух компонент – энтропийных мер хаотичности и самоорганизации:

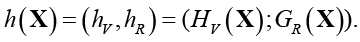(3)

Векторная энтропийная модель (1)–(3) учитывает все основные закономерности сложных систем [17, c. 34–43].

Рентгенологические и ультразвуковые показатели представлены в виде балльных значений. Поэтому при вычислении дифференциальных энтропий HV(Xj) используем методику, приведенную в [22], а при вычислении парных корреляций между показателями считаем, что для каждого балльного значения соответствующие фактические значения показателя имели некоторое гауссово распределение [23, с. 54–59].

Группы рентгенологических и ультразвуковых показателей можно интерпретировать как подсистемы в системе всех показателей. Поэтому для диагностирования биотипа РМЖ можно использовать энтропийную меру связи между этими группами [17, с. 97–98]:

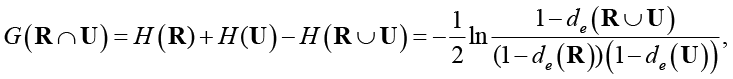(4)

где 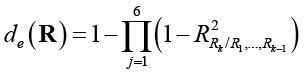, 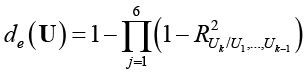– коэффициенты тесноты корреляционной связи между компонентами случайных векторов R и U.

Если R и U – гауссовы случайные векторы, имеем

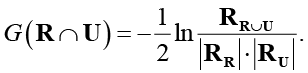(5)

Согласно (4): 1) если между компонентами случайных векторов R и U отсутствует строгая функциональная связь, но хотя бы одна компонента коррелирована Rj хотя бы с одной компонентой Uk, то 0 < G(R ∩ U) < ∞ ; 2) если хотя бы одна компонента Rj строго функционально связана хотя бы с одной компонентой Uk, то G(R ∩ U) = ∞ ; 3) если все компоненты случайного вектора R взаимно независимы с компонентами случайного вектора U, то G(R ∩ U) = 0 ; 4) чем теснее корреляционная связь между компонентами случайных векторов R и U, тем больше значение G(R ∩ U).

Результаты исследования и их обсуждение

Выполним классификацию больных по пяти биотипам на основе линейного дискриминантного анализа. Для сопоставимости данных нормализуем показатель T (возраст пациентки) – приведем выборку к минимуму, равному 0, и единичной дисперсии. Решение состоит в нахождении такой совокупности показателей, которая позволила бы (если это возможно) статистически достоверно распознать различия в этих группах. В табл. 2 представлены результаты дискриминантного анализа пяти биологических подтипов больных.

Параметр Wilks’ lambda (λ, лямбда Уилкса, статистика Уилкса) принимает значения от 0 до 1. Чем меньше λ, тем лучше разделяются данные на пять кластеров. Значения параметра в целом по показателям λ = 0,509, что свидетельствует о неудовлетворительном результате классификации данных. В первом столбце (Wilks’ lambda) табл. 3 приведены значения статистика Уилкса с исключенной соответствующей переменной. Во втором столбце (Partial Lambda) приведены значения частной лямбды Уилкса. Данная статистика описывает одиночный вклад соответствующей переменной в дискриминацию между совокупностями. Чем она меньше, тем больше вклад показателя в общую дискриминацию, видим, что ни одна из переменных не позволяет разделить совокупность многомерных данных на пять групп.

Таблица 2

Результаты дискриминантного анализа, λ = 0,509; F(40, 1332) = 6,489; p < 0,000

Источник: составлено авторами на основе полученных данных в ходе исследования.

Таблица 3

Результаты классификации данных на пять биотипов

Источник: составлено авторами на основе полученных данных в ходе исследования.

В следующих двух столбцах приведены F-статистики (F-remove) дисперсионного анализа и соответствующие p-уровни, характеризующие вклад каждой из переменных в различие двух групп. В соответствии с результатами наиболее значимыми являются показатели R2, R3, T. Значение толерантности (Toler) показателя вычисляется как 1 – R2, где R2 – коэффициент детерминации линейной регрессии этого признака Xi на оставшуюся совокупность статистически значимых признаков, использованную в анализе.

В табл. 3 приведены результаты классификации данных.

Из табл. 3 видим, что только 61,4 % пациенток были правильно классифицированы. А для биотипа 4 правильно классифицирована только одна пациентка из 21. Таким образом можно говорить о неудовлетворительной классификации больных на биотипы РМЖ.

Энтропийный анализ проведем по всем популяциям пациенток для всех пяти биологических подтипов. Из-за линейной зависимости и постоянства значений для всех пациенток биотипа исключим по два показателя из каждой группы. В результате будем рассматривать четыре рентгенологических 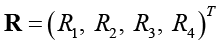и четыре ультразвуковых 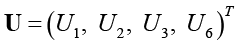показателя. Для энтропийного анализа в рамках соотношений (1)–(5) достаточно для всех пяти биотипов определить корреляционные матрицы и вычислить среднеквадратические отклонения рентгенологических и ультразвуковых показателей. Это легко реализуется даже средствами MS Excel.

В табл. 4 приведены рассчитанные по формулам (2), (4), (5) энтропийные показатели для всех биотипов РМЖ. Видим, что во многих случаях показатели для разных биотипов существенно различаются. Поэтому сравним попарно показатели между биотипами. Будем считать, что значения показателя у двух биотипов существенно различимы, если они отличаются хотя бы в 1,9 раза.

На рисунке для каждого из подтипов приведены значения всех пяти показателей Yi(k,j), рассчитанных по табл. 4. Логарифмирование позволяет легко интерпретировать рисунки – если значение показателя не ниже 1, то это означает существенное различие между соответствующими подтипами. В табл. 5 дана сводка значимых попарных отношений энтропийных показателей из рисунка.

Таблица 4

Энтропийные показатели для всех биотипов

Источник: составлено авторами на основе полученных данных в ходе исследования.

Значения всех пяти показателей Yi(k,j) для каждого из подтипов

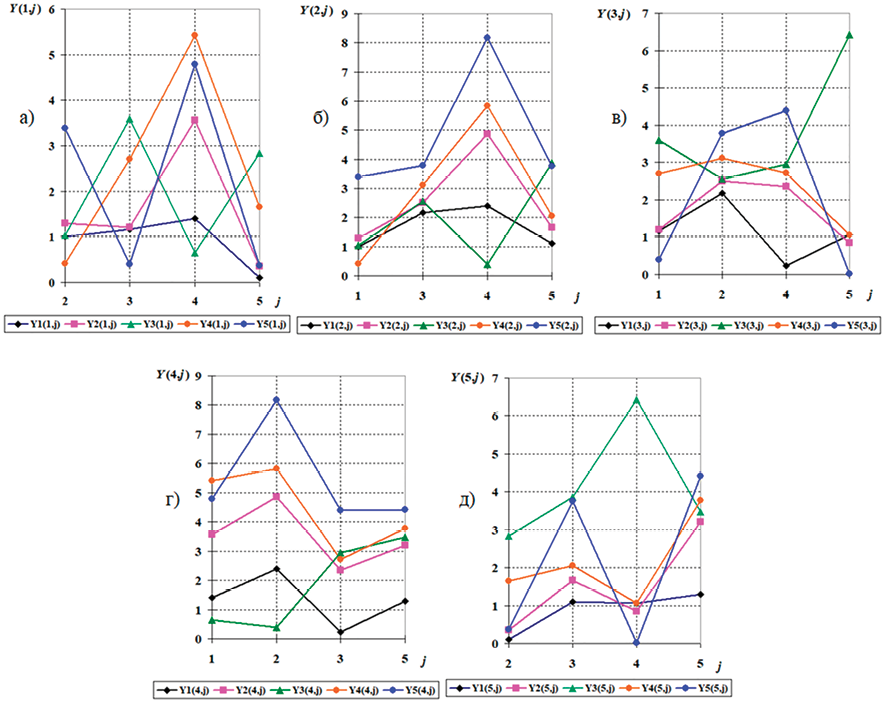
Обозначим , ,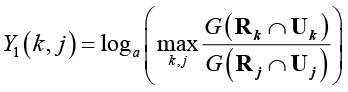

, ,

, .

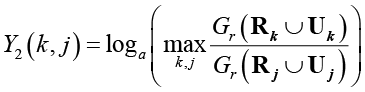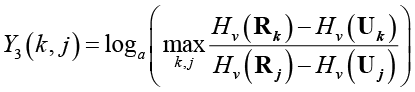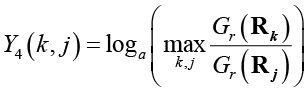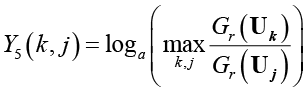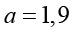Из табл. 5 видно, что от 2 до 5 раз энтропийные показатели между всеми биотипами различаются более чем в 2 раза.

Таблица 5

Сводка значимых попарных отношений энтропийных показателей

Источник: составлено авторами на основе полученных данных в ходе исследования.

Заключение

Проведенное комплексное исследование проблемы лучевой диагностики рака молочной железы с применением современной технологии математического моделирования и вычислительного эксперимента показало следующее. Неудачное использование линейной классификации данных свидетельствует о наличии корреляций между используемыми рентгенологическими и ультразвуковыми показателями. Векторное энтропийное моделирование показало, что множества рентгенологических и ультразвуковых показателей у пяти биотипов РМЖ имеют различия на системном уровне. Проанализированы пять энтропийных показателей. Оказалось, что не менее чем в двух случаях эти энтропийные показатели между всеми биотипами попарно различимы. Это позволяет в дальнейшем разработать количественные критерии неинвазивной диагностики биотипов РМЖ на начальной стадии заболевания. Результат может быть достигнут за счет совместного использования двух рассмотренных методов математического моделирования – линейного дискриминантного анализа и векторного энтропийного моделирования. Для повышения достоверности этих критериев в дальнейшем желательно увеличить обучающие выборки больных для 3, 4, 5-го биотипов, а также привести используемые в рамках исследования наборы данных.