Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 1,172

Введение

Ужесточение политики Запада в отношении России усиливает актуальность проблемы сырьевой безопасности в алюминиевой промышленности. Так, например, в планах РУСАЛа замещение импорта глинозема его производством на территории России из алюмосиликатного сырья. Планируется создание на территории Красноярского края завода по производству глинозема из каолиновой руды с годовой мощностью 1 млн т. Другой предполагаемый вид сырья – зола [1].

Сырьевой дефицит мотивирует научно-исследовательские работы по созданию технологической безопасности страны в области переработки различных видов сырья с получением полезных продуктов [2; 3]. В Институте геологии и природопользования ДВО РАН изучается фторидно-аммониевая технология алюмосиликатов и ее применение для переработки золы сжигания углей ТЭС ввиду их значительного накопления в Амурском регионе и заметного содержания в ней широкого спектра химических элементов, в том числе редких, что является предметом большого интереса [4–6].

Цель исследования – проведение термодинамического и кинетического анализа физикохимии фторидно-аммониевой переработки золы. Наиболее важными являются спекание золы с гидродифторидом аммония NH4HF2 [7] и процесс термообработки спека с разложением гексафтороалюмината аммония (NH4)3AlF6 и сублимацией гексафторосиликата аммония (NH4)2SiF6 [8]. С этими реакциями связаны основные достоинства данной технологии.

Материалы и методы исследования

Перед проведением эксперимента авторами проводился термодинамический расчет с определением вероятных направлений реакции в зависимости от температуры. Вычислялись температурные изменения энергий Гиббса ΔGT

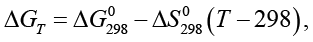(1)

где 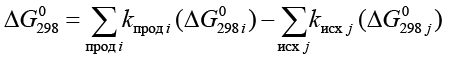– разность термодинамических потенциалов Гиббса продуктов и исходных веществ при 298 К, 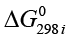и 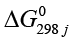– энергия Гиббса образования 1 моля данного продукта и данного реагента из простых веществ в стандартных условиях соответственно,

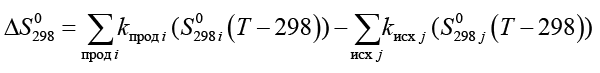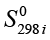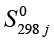– разность суммарных энтропий продуктов и исходных веществ, и – значения молярной энтропии для данного продукта и данного реагента соответственно при стандартных условиях [9].

Эти изменения энергий Гиббса для реакций фторирования основных компонентов золы и реакции разложения с сублимацией фторидно-аммониевых солей приведены в табл. 1. Из табл. 1 видно, что реакции спекания (1–5) идут в прямом направлении, скорость реакций (1, 3–5) увеличивается с ростом температуры, скорость второй реакции почти не меняется с ростом температуры, немного уменьшается. Реакция разложения гексафтороалюмината аммония (6), согласно расчету, начинается при температуре 267 ºС.

Таблица 1

Расчетные значения изменений потенциала Гиббса ΔG (кДж) для реакций фторидно-аммониевой переработки золы. Температуры приведены в ºС

Источник: составлено авторами на основании расчетов энергий Гиббса по формуле (1).

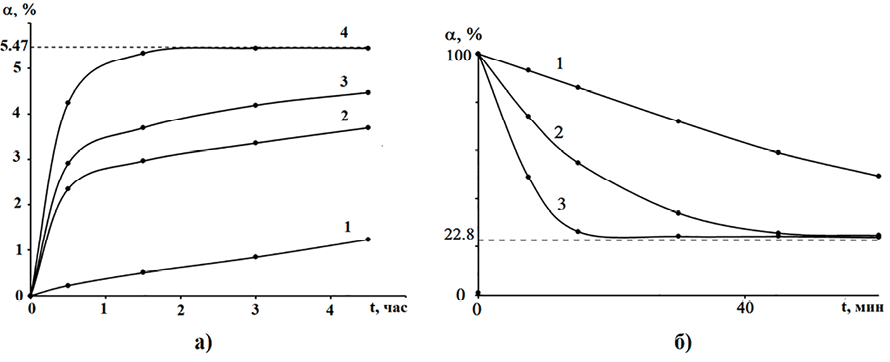
Интегральные кинетические кривые для реакций а) спекания золы с гидродифторидом аммония для температур: 1 – 50 ºС, 2 – 100 ºС, 3 – 150 ºС и 4 – 200 ºС; б) разложения с сублимацией фтор-аммониевых солей при температурах: 1 – 350 ºС, 2 – 450 ºС, 3 – 550 ºС Источник: составлено авторами на основании экспериментальных исследований

Фторирующим реагентом являлся гидродифторид аммония, более экологичный и менее агрессивный, чем фтор или плавиковая кислота [10], фторируемым реагентом являлась зола, состав которой приведен в [11].

Время спекания 0,5–4,5 ч, температуры 50–200ºС. Рентгенофазовый анализ показал, что результатом спекания (процесс протекал по реакции 1–5–5) являлся твердый спек фторидно-аммониевых солей алюминия и кремния, флюорита (Ca, Y)F2, магнетита и фторидов NaF и KF, улетучивались аммиак NH3, фтороводород HF и водяной пар H2O.

Разложение гексафтороалюмината и сублимация гексафторосиликата аммония (по уравнению (6) из табл. 1) проходили при термообработке (350–550 ºС) образовавшегося при спекании твердого осадка. Газообразные продукты разложения гексафтороалюмината аммония улетучивались и собирались в сосуде с водой, а сублимат гексафторосиликата аммония осаждался на холодных стенках сосуда. После удаления летучих продуктов переработка продуктов твердых (смесь фтористого алюминия с ранее упоминавшимися магнетитом, флюоритом и щелочными фторидами Na и K) с получением полезных продуктов подробно описана в [9; 11].

В обеих реакциях навеска взвешивалась, измерялось уменьшение ее массы m, которое далее пересчитывалось в степень превращения вещества (СПВ) α по формуле α = (m / m0) × 100%, где m0 – расчетное значение массы. Временная зависимость СПВ в ходе фторирования описывается кривыми на рисунке, а, а в ходе разложения и сублимации – кривыми на рисунке, б. В результате математической обработки экспериментальных данных, по которым построены интегральные кинетические кривые на рисунке, а и б, получаем кинетические характеристики этих реакций.

При расчете использовался параметрический регрессионный и корреляционный анализ (ПРКА), а также проверялись статистические гипотезы Фишера, Снедекора – Фишера и Стьюдента [12, с. 362]. В качестве параметрических функций (ПФ) αi(t) авторами ранее в работе [7] выбирались степенная (i = 0) и экспоненциальная (i = 2), уравнения Ерофеева – Авраами (i = 1), трехмерной диффузии (i = 3) и сжимающейся сферы (i = 4). Также, учтя форму интегральной кривой 1 на рисунке, а, близкую к прямой линии, к этим ПФ авторами в данной работе добавлен линейный закон (i = 5). Правда, учитывая более ярко выраженную нелинейность интегральных кинетических кривых при других температурах, линейный закон применим, по-видимому, только для нижней температуры эксперимента по спеканию

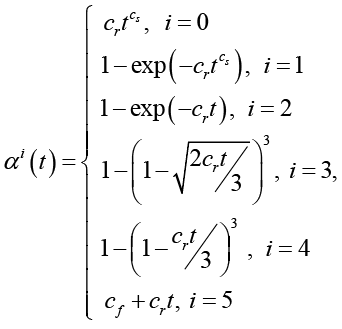(2)

где αi(t) – i-я ПФ, cr, cs и cf – константа скорости, коэффициент формы и свободный член соответственно [13]. На основе этих ПФ аналогично [6; 10] строилась модель обобщенной линейной регрессии (МОЛР)

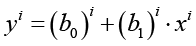, (3)

где в формуле (3) индекс i (i=0, 1, …, 5) нумерует МОЛР, соответствующие ПФ αi(t), (b0)i и (b1)i – первый и второй коэффициенты МОЛР; xi(t) и yi(t) – обобщенные абсциссы и ординаты, задаваемые формулами

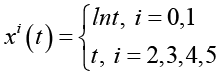(4)

и

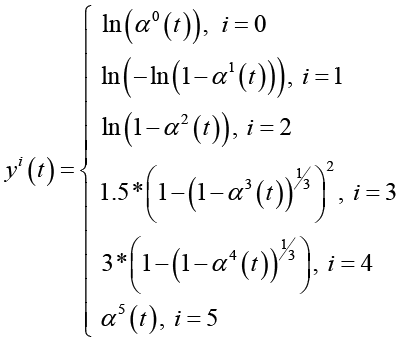(5)

Точечные оценки (ТО) коэффициентов МОЛР (b0*)ji, (b1*)ji рассчитывались методом наименьших квадратов из уравнения (3), в котором

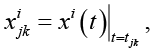а ,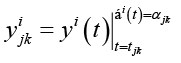

индексы j (j = 0,1,...,m) и k (k = 0,1,...,nj) отмечают исследуемые температуры Tj и моменты отсчетов времени (МОВ) tjk соответственно, а tjk и αjk – экспериментальные массивы данных о МОВ и СПВ соответственно, имеющих размерность (nj ; m).

ТO (cr*)ji, (cs*)ji и (cf*)ji кинетических характеристик cr, cs и cf соответственно для i-й МОЛР при j-й исследуемой температуре Tj рассчитывались по следующим формулам

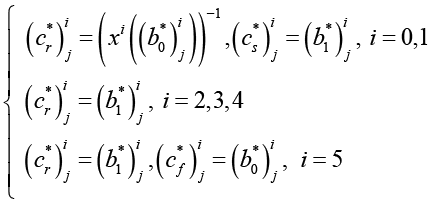
. (6)

Подставив ТО (cr*)ji, (cs*)ji и (cf*)ji в уравнение для i-й ПФ αi(t) при температуре Tj получим уравнение для функции отклика:

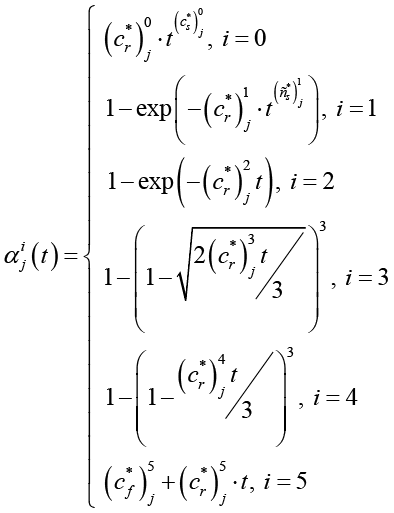(7)

Энергии активации Ei рассчитывались по уравнению Аррениуса [14, с. 83]:

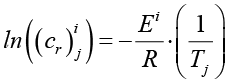. (8)

Выбор при исследуемой температуре Tj МОЛР (3) осуществлялся с минимальной погрешностью аппроксимации [11, с. 394], рассчитываемой как среднее относительное отклонение функций отклика от экспериментальных значений СПВ:

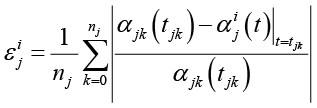, (9)

где 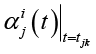– значения i-й функции отклика αij(t) при t = tjk.

Расчетные формулы для погрешностей коэффициентов МОЛР, кинетических и статистических параметров с последующей проверкой статистических гипотез приведены в работе [11].

В данной работе авторами добавлен ряд ранее не использованных статистических величин. Одна из них – индекс детерминации, величина, которая характеризует долю факторной дисперсии в общей дисперсии [12, с. 392]:

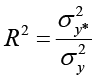,(10)

где 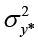– факторная дисперсия, 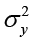– общая дисперсия. Также используется индекс корреляции (ИК)

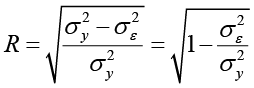,(11)

где 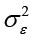– остаточная дисперсия. Значимость ИК оценивается по показателю согласованности Фишера

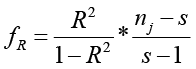,(12)

где s – число коэффициентов в уравнении регрессии. Входами в таблицу распределения Фишера [12, с. 484–486] при заданном уровне доверительной вероятности α служат величины 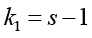и 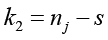. Если 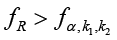, то величина ИК признается значимой [12, с. 392].

Результаты исследования и их обсуждение

Химические реакции фторирования и разложения с сублимацией фторидно-аммониевых солей подробно описаны в [10]. Ход кинетических кривых этих реакций, как интегральных, так и дифференциальных, полученных авторами, проанализирован в [10] на основе данных [15, с. 74].

В работе [11] приведены результаты вычислений с ПФ, которые имеют индекс i = 0, …, 2 в выражении (2). В статье [7] эти результаты дополнены ПФ с i = 3, 4 (соответственно уравнениями непрерывной диффузии и сжимающейся сферы). Данная работа дополняет выполненные ранее исследования шестой ПФ c i = 5 (линейным законом).

После того, как кинетические и статистические характеристики рассчитаны и выбрана ОЛРМ с наименьшей погрешностью аппроксимации, проводится проверка каждой из девяти статистических гипотез. Проверяется, как и ранее в [11], однородность дисперсии воспроизводимости и адекватность МОЛР, значимости обоих коэффициентов МОЛР, сила связи между входной и выходной переменными по величине коэффициента корреляции (КК), значимость КК. Кроме того, авторами принимаются в рассмотрение также индекс детерминации, который показывает долю вариации выходной переменной, которая обусловлена вариацией входной переменной, расчет индекса корреляции (ИК) Фишера и проверка гипотезы о его значимости.

Отметим, что количество статистических параметров, оценивающих регрессионные модели, велико и зависит от количества проверяемых гипотез, в работе [11] использовалось 6 гипотез, в данной работе 9, при четырех исследуемых температурах приходится оперировать с 36 значениями статистик и 9 значениями критических точек. Поэтому есть смысл ввести суммарную характеристику, комплексно оценивающую исследуемую модель, принимающую значения от 0 до 100 %, предполагая равные вклады различных гипотез. Предположение о равных вкладах представляется естественным, так как гипотезы выбраны неслучайно, каждая имеет существенное значение. Поясним их выбор. Традиционными являются гипотезы Фишера и Снедекора – Фишера об однородности дисперсии воспроизводимости и об адекватности регрессионной модели, которые определяют применимость регрессионного анализа. Далее, рассматриваются гипотезы о влиянии факторов при помощи индекса детерминации Фишера и по t-критерию Стьюдента о значимости коэффициентов регрессии (углового коэффициента и постоянного члена). Кроме того, проверяется гипотеза о достоверности функции отклика при помощи КК и показателя согласованности Стьюдента, с одной стороны, а также ИК и показателя согласованности Фишера, с другой стороны. Если соответствующая гипотеза при сравнении значения ее статистики с критическими значениями коэффициентов Фишера или Стьюдента соответственно отвергается, то ее вклад в суммарную статистику равен нулю, если принимается, то равен приблизительно 11,11 %, так как всего проверяемых гипотез 9 (100 % / 9 = 11,11 %). Среди девяти характеристик гипотез имеются индекс детерминации, ИК и КК, которые сравниваются с величиной 0,7. Если меньше, то влияние входного фактора пренебрежимо мало и вклад нулевой, если больше или равно, то вклад равен 11,11 %. Вклады суммируются и округляются до целых величин. В итоге, если суммарная статистика в эксперименте при данной температуре равна 100 %, на значения статистик при данной температуре можно не отвлекаться. В табл. 2 авторами показаны значения кинетических параметров для исследуемых реакций и статистик, суммирующих вклады всех проверяемых гипотез. Как показывает таблица, реакция фторирования при температурах 100, 150 и 200 ºС подчиняется степенному закону, при этом ее энергия активации 13 кДж/моль, а при температуре 50 ºС – линейному закону, при этом ее энергия активации 4 кДж/моль, ход реакции при всех температурах определяется диффузией.

Таблица 2

Кинетические и статистические характеристики для реакций спекания золы с ГДФА и разложения с сублимацией фторидно-аммониевых солей

Источник: составлено авторами на основании расчетов кинетики по формулам (2)–(9) и статистики по формулам в работе [11], а также по формулам (10)–(12) в данной работе. Столбец 2 (Tj = 50 ºС) и строка «Суммарная статистика» являются оригинальными.

Термическая обработка, в ходе которой разлагается гексафтороалюминат аммония и сублимирует гексафторосиликат аммония, определяется как процессами диффузии частиц, так и химическим взаимодействием веществ, то есть зона переходная, реакция подчиняется уравнению Ерофеева – Авраами, энергия активации 31 кДж/моль.

Равенство суммарных статистик 100 % во всех температурных диапазонах означает, что все гипотезы выполняются. Результаты статистической проверки второй реакции говорят, что при температурах 350 и 450 ºС все гипотезы принимаются, но при верхней температуре суммарная статистика равна 89 %, менее 100 %, что значит, что не все гипотезы проходят проверку. Проверяя все гипотезы при температуре 550 ºС, например используя таблицу из работы [9], приходим к выводу, что нарушается гипотеза о достоверности функции отклика, так как оказывается незначимым КК (значение показателя согласованности Стьюдента 3,11 меньше коэффициента Стьюдента 4,3). Однако выполняется добавленная авторами гипотеза Фишера о значимости ИК (значение показателя согласованности Фишера 24,69 больше, чем коэффициент Фишера 9,55). Следует отметить, что в данной работе для оценки достоверности функции отклика дополнительно к более популярным КК и показателю согласованности Стьюдента используются также ИК и показатель согласованности Фишера, и данный случай интересен тем, что по критерию Стьюдента достоверность функции отклика отвергается, а по критерию Фишера принимается.

Заключение

Топохимический расчет неизменно сопровождает технологию переработки сырья или техногенных отходов с использованием фторидно-аммониевых солей. Программа на языке Visual Basic, созданная авторами в среде Visual Studio, дополнена авторами для расчетов с новой параметрической функцией и новых статистических величин, в том числе суммарной статистики. При расчетах используется ПРКА, проверяется достоверность девяти статистических гипотез Фишера, Снедекора – Фишера и Стьюдента. Поскольку проверяется большое количество статистических параметров, некоторые гипотезы нарушаются в каких-то температурных диапазонах. Поэтому имеет смысл введение обобщенной статистики, которая суммирует результаты проверки отдельных гипотез. Убедительным результатом статистической проверки, по-видимому, может считаться суммарная статистика не менее 70 %.