Введение
В настоящее время для исследования космического электромагнитного излучения в различных частотных диапазонах широко применяются методы математического моделирования [1, с. 9; 2, с. 30]. Наиболее простым и наглядным методом моделирования транспорта излучения является лучевое приближение [3, с. 72; 4, с. 39]. С его помощью можно отследить динамику высокочастотной асимптотики волнового поля в космической среде. Необходимым условием применимости геометрической оптики является предположение о медленном изменении показателя преломления среды в масштабе длины волны. Лучевой метод эффективно используется в задачах распространения излучения в атмосферах Земли и других планет [3, с. 91; 5; 6, с. 157]. Построение лучевых траекторий положено в основу метода просвечивания околосолнечной плазмы [7–9]. Траекторные расчеты нашли применение в задачах зондирования солнечного ветра [10]. Лучевые представления позволяют одновременно исследовать эффекты космической плазмы и особенности проявления кривизны пространства в структуре электромагнитного излучения галактических и внегалактических источников [1, с. 65; 11; 12]. В ряде случаев при реализации геометрической оптики вводятся различные дополнительные приближения, позволяющие существенно повысить оперативность расчетов траекторий лучей, которые описывают рефракцию излучения в неоднородной среде. В частности, одним из таких приближений является применение локальной (квазисферической) системы координат [4, с. 87; 11; 12]. Основой локального приближения является предположение, что излучение распространяется в основном в плоскости дуги большого круга, то есть в плоскости, проходящей через центр сферической системы координат, источник и пункт наблюдения [6, с. 45]. Для убедительной интерпретации данных радиоастрономических и астрофизических экспериментов особенно важен высокоточный расчет рефракции электромагнитного излучения при распространении в трехмерно-неоднородной космической среде. Поэтому требуется анализ достоверности локального приближения в условиях, когда плоскость падения излучения наклонена относительно плоскости дуги большого круга.
Цель исследования – оценка возможностей квазисферического приближения для расчета рефракционных характеристик космического излучения при распространении в поле тяготения астрофизических объектов.
Материалы и методы исследования
В данном исследовании использован метод геометрической оптики [3, с. 72] для расчета влияния поля тяготения массивного объекта на рефракцию электромагнитного излучения. Траекторная задача решена в евклидовом пространстве путем введения эффективного показателя преломления вакуума, выраженного через гравитационный потенциал. В качестве математического аппарата использованы нелинейные обыкновенные дифференциальные уравнения первого порядка, полученные из вариационного принципа Ферма [13, с. 305]. Численное интегрирование лучевых уравнений выполняется классическим методом Рунге – Кутты 4-го порядка точности с использованием функции odeint (модуль scipy.integrate языка Python) [14]. С помощью численного моделирования удается эффективно визуализировать лучевую структуру излучения точечного источника в картинной плоскости наблюдателя для широкого набора параметров задачи. Наряду со строгими численными расчетами, для приближенного синтеза лучевой картины применяется локальная (квазисферическая) система координат [6, с. 45], позволяющая описать процесс распространения излучения в окрестности плоскости дуги большого круга, проходящей через центр сферической системы координат, источник и пункт наблюдения.
Результаты исследования и их обсуждение
Для оценки границ применимости локального приближения получим вначале лучевые дифференциальные уравнения из вариационного принципа Ферма [13, с. 305]:
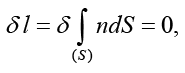(1)
где δl – вариация оптического пути распространения; n – показатель преломления космической среды; dS – элемент дуги. Учитывая, что dS в случае сферической системы координат имеет вид
,
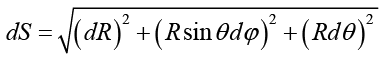где R, φ, θ – соответственно радиальная, азимутальная и полярная угловые координаты луча, выражение (1) можем записать в виде
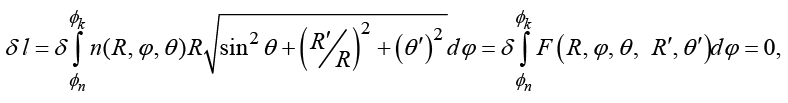(2)
где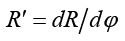 
, 
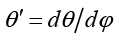, φn, φk – начальная и конечная угловые координаты пунктов излучения и приема, соответственно. Распишем выражение (2):
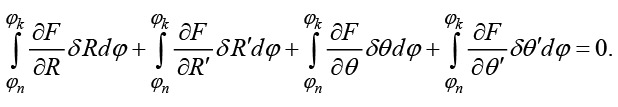(3)
Используя (3), получим путем известных преобразований систему дифференциальных уравнений Эйлера:
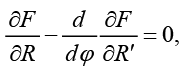
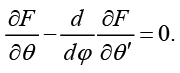(4)
Соответствующие частные производные имеют вид
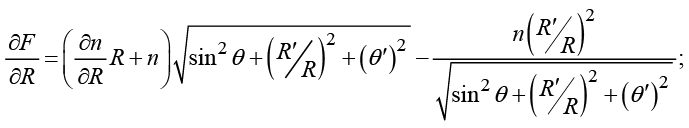
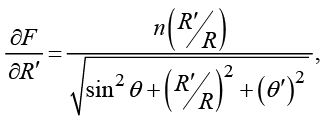
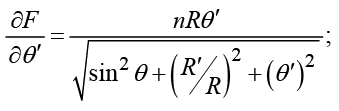(5)
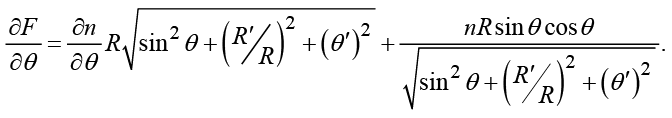
Подставляя выражения (5) в систему (4), получим дифференциальные уравнения вида
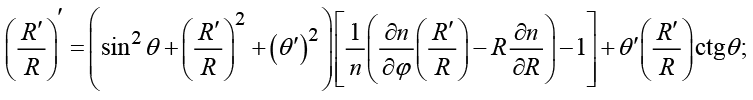(6)
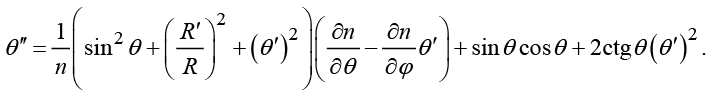
Вводя текущие углы рефракции α, β, из системы (6) получим лучевые дифференциальные уравнения в форме Лагранжа – Эйлера в сферической системе координат:
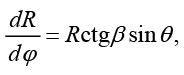
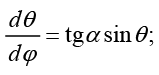
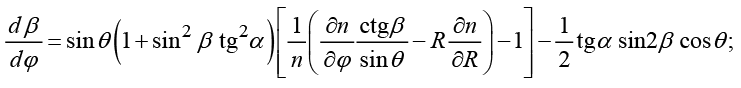(7)
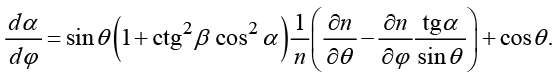
Для оперативности и наглядности расчетов рефракции космического излучения в различных средах нередко используется квазисферическая система координат [6, с. 45] и полагается, что траектории лучей сосредоточены в окрестности плоскости дуги большого круга, проходящей через источник, приемник и центр сферической системы координат (θ(φ = 0) = π/2). В этом случае для элемента дуги имеем
.
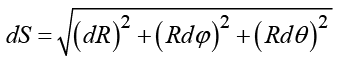Проводя аналогичные аналитические преобразования, что и при выводе (7), получим систему лучевых уравнений в квазисферической системе координат. С учетом упрощенной записи элемента дуги dS вариационный принцип (2) принимает вид
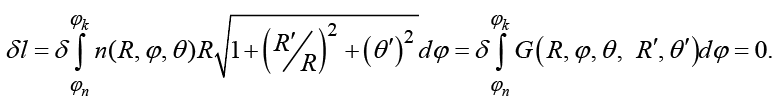(8)
Расписывая выражение (8) с подынтегральной функцией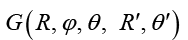 
, имеем
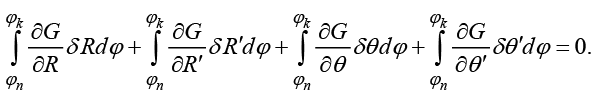(9)
Используя (9), получим систему дифференциальных уравнений Эйлера:
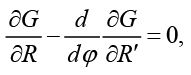
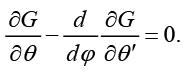(10)
В этом случае входящие в систему (10) частные производные принимают вид
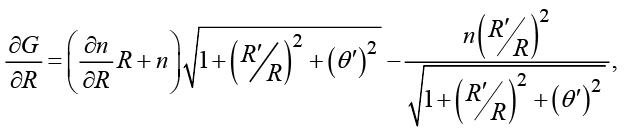(11)
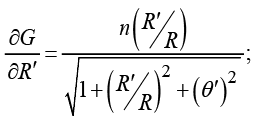
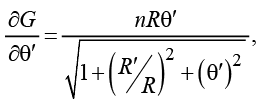
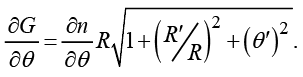
Решая систему (10) с учетом выражений (11), получим дифференциальные уравнения вида
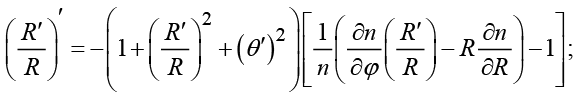(12)
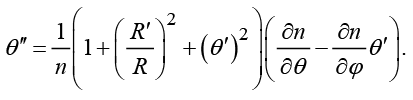
Путем введения текущих углов рефракции α, β из системы (12) получим лучевые уравнения в квазисферическом приближении [12]:
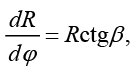
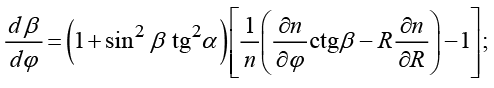(13)
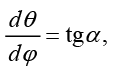
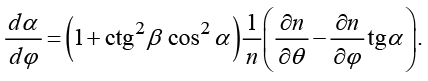
Отметим, что в случае θ(φ = 0) = π/2 система (7) переходит в систему (13).
Анализ возможностей применения квазисферической системы координат для расчетов рефракционных характеристик космического излучения был проведен в наиболее информативном случае распространения электромагнитного излучения в поле тяготения одиночного астрофизического объекта. Как известно [15, с. 170], согласно общей теории относительности (ОТО) для слабых гравитационных полей задача рефракции излучения в окрестности астрофизического объекта может быть решена в обычном евклидовом пространстве путем введения эффективного показателя преломления вакуума.
Численные расчеты на основе систем уравнений (7), (13) были выполнены с использованием модели эффективного показатель преломления вида
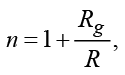(14)
где Rg – гравитационный радиус массивного объекта. Геометрия задачи и схематическое изображение лучевых траекторий показаны на рис. 1.
Численное интегрирование уравнений (7), (13) проводилось методом Рунге – Кутты 4-го порядка точности [16, с. 363] с использованием функции odeint (модуль scipy.integrate языка Python) [14], предназначенной для решения систем обыкновенных дифференциальных уравнений первого порядка. Численные расчеты были выполнены с начальными условиями: R(φ = 0) = Rn = 50cul (cul – условная единица длины), θ(φ = 0) = π/2 + Δθ (система (7)) и θ(φ = 0) = Δθ (система (8)), α(φ = 0) = αn, β(φ = 0) = βn. Значения начальных углов излучения αn варьировались в диапазоне [–0.75; 0.75], а углов βn – в диапазонах [–0.75; 0.06] и [0.06; 0.75]. Смещение начального значения полярной координаты Δθ рассматривалось в диапазоне [0.0; 0.5]rad. Расчеты проводились для случая Rg = 1cul до расстояния Rk = 50cul, где фиксировались конечные значения угловых координат (φk; θk). Для наглядности результаты моделирования представлялись в виде проекции в картинной плоскости наблюдателя посредством перерасчета конечных значений координат луча:
, 
.
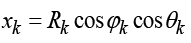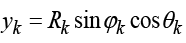Результаты расчета представлены на рис. 2, где красными кружками обозначены проекции точек прихода лучей на фиксированное расстояние Rk, полученные посредством системы (7), а черными кружками – с применением системы (13).
Анализ рис. 2 показал, что с увеличением смещения начального значения полярной угловой координаты ошибка расчета лучевых траекторий с использованием приближенной системы (13) возрастает. Эта погрешность соответственно приводит к возникновению отличий и в лучевой структуре излучения в картинной плоскости наблюдателя. Проявляющиеся тонкие эффекты в центральных областях лучевой картины, рассчитанные на основе строгой системы (7), становятся более заметными при меньших смещениях начальной полярной координаты, чем при расчетах с использованием системы (13).
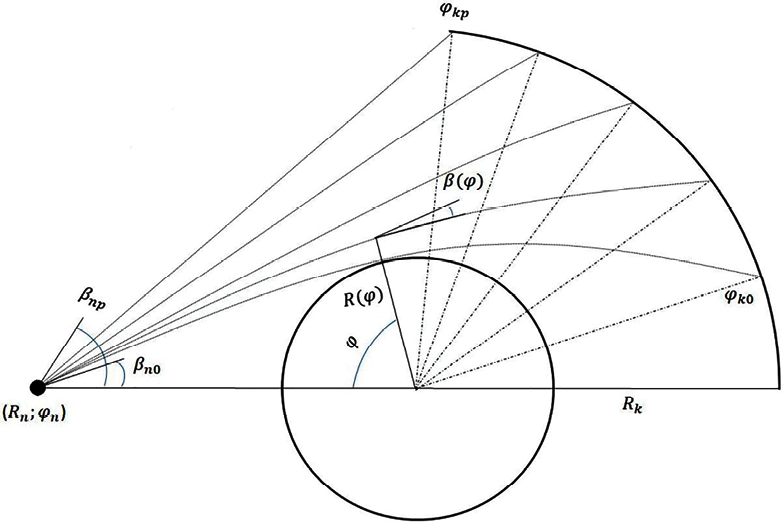
Рис. 1. Геометрия задачи. Вид сбоку. (Rn; φn) – координаты источника излучения относительно центра массивного объекта; Rk – расстояние до сферической поверхности; [φk0; φkp] – распределение конечных угловых координат лучей на сферической поверхности; [βn0; βnp] – диапазон начальных углов излучения; R(φ), φ, β(φ) – соответственно текущие значения радиальной и угловой координат луча, а также угла рефракции Источник: составлено авторами по результатам данного исследования
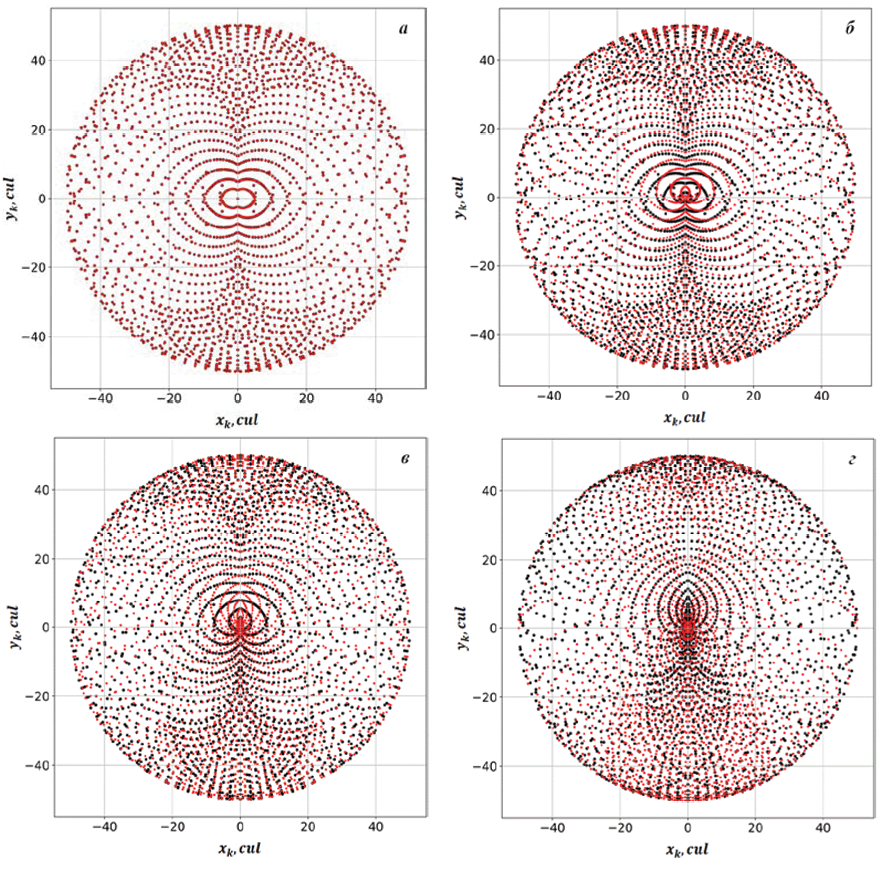
Рис. 2. Картинная плоскость наблюдателя при распространении излучения в поле тяготения астрофизического объекта при различных значениях Δθ: а – 0rad; б – 0.03rad; в – 0.3rad; г – 0.5rad Источник: составлено авторами по результатам данного исследования
Между тем общий интегральный эффект воздействия поля тяготения одиночного астрофизического объекта на рефракционные характеристики излучения в обоих случаях сохраняется с достаточной точностью до значений смещения Δθ ± 0.3rad. Этот результат позволяет в ряде случаев при интерпретации данных измерений характеристик космического излучения [1, с. 74; 17] использовать результаты математического моделирования, полученные в приближении локальной (квазисферической системы координат).
Заключение
Сделана оценка возможностей локального (квазисферического) приближения геометрической оптики для расчета рефракционных характеристик космического электромагнитного излучения при распространении в поле тяготения массивного объекта. Выполнен детальный сравнительный анализ аналитических преобразований при выводе строгих и приближенных систем лучевых дифференциальных уравнений в форме Лагранжа – Эйлера из вариационного принципа Ферма. На основе систем лучевых уравнений проведено численное моделирование рефракционных характеристик космического излучения прошедшего поле тяготения одиночного гравитационного объекта. Показано, что в квазисферическом приближении лучевая структура излучения в картинной плоскости наблюдателя соответствует строгим расчетам, когда плоскость падения излучения наклонена относительно плоскости дуги большого круга не более, чем ± 0.3rad.