Введение
Проблема нахождения области корней полинома актуальна для численного анализа и вычислительной алгебры, решение этой проблемы требуется во многих методах теоретических и прикладных исследований [1, с. 16; 2, с. 295]. Поиск опирается на фундаментальные положения алгебры: «Полином с комплексными коэффициентами, отличный от постоянной, имеет по меньшей мере один комплексный корень» [3, с. 218], и «Полином n-й степени имеет ровно n корней, действительных или комплексных, при условии, что каждый корень считается столько раз, какова его кратность» [4, с. 158]. Непосредственно ниже полином рассматривается в виде
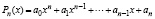, (1)
где коэффициенты – действительные числа, причем a0 ≠ 0. Приведенные утверждения являются теоремами существования, что не влечет конструктивных методов вычисления корней. Большинство методов вычисления являются приближенными. Прежде чем вычислять корень, необходимо знать, где он расположен. Отсюда методы делятся на вычислительные приближения корней и на оценки области расположения корней, которые излагаются в академических и учебных изданиях. Так, методы вычисления корней алгебраических и трансцендентных функций описаны в [4, с. 112], там же даны методы определения области корней [4, с. 158]. Для определения границ области корней, в частности, приняты следующие оценки: «Пусть
,
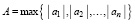где ak – коэффициенты полинома (1). Тогда модули всех корней xk полинома (1) удовлетворяют неравенству
,
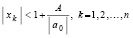то есть корни этого полинома на комплексной плоскости лежат внутри круга
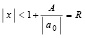» [4, с. 159].
Следствие: «Пусть
.
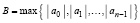Тогда все корни xk полинома (1) удовлетворяют неравенству
,
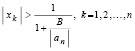то есть все корни этого полинома расположены в круговом кольце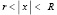 
» [4, с. 159]. Оценка Маклорена: «Пусть аргумент и коэффициенты полинома (1) являются действительными, причем a0 > 0. Если Pn(x) не имеет отрицательных коэффициентов, то отсутствуют положительные корни, так что верхней оценкой для вещественных корней оказывается число 0. Пусть отрицательные коэффициенты имеются, m – номер первого по порядку отрицательного коэффициента и A – максимум модуля отрицательных коэффициентов. Тогда действительные корни Pn(x) не превосходят 
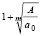» [3, с. 223].
К числу основополагающих оценок области действительных корней полинома относятся теоремы Штурма и Бюдана – Фурье.
Последовательность f0, f1, …, fk Штурма полиномов, построенных для данного полинома Pn(x) = f0, удовлетворяет следующим требованиям при значениях x из данного интервала (a, b): 1) последний полином fk не обращается в нуль; 2) два соседних полинома не обращаются в нуль одновременно; 3) если некоторый полином fi, 1 ≤ fi ≤ k–1, обращается в нуль в некоторой точке x0, то соседние полиномы fi–1 и fi+1 имеют в x0 значения противоположных знаков; 4) произведение f0 f1 меняет знак с минуса на плюс, когда x, возрастая, проходит через корень полинома f0 [3, с. 225].
Теорема Штурма [3, с. 225]. Число корней полинома Pn(x) в промежутке [a, b] равно числу перемен знаков в значениях ряда Штурма при x = a минус число перемен знаков при x = b. Предполагается, что концы промежутка не являются корнями Pn(x).
Теорема Бюдана – Фурье [4, с. 172]. Если числа a и b (a<b) не являются корнями полинома Pn(x) из (1), то число N(a, b) действительных корней этого полинома, содержащихся между a и b, равно минимальному числу ΔN перемен знаков, потерянных в системе последовательных производных
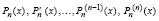(2)
при переходе от x = a к x = b, или меньше числа ΔN на четное число, то есть
,
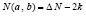где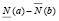 
и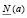 
– нижнее число перемен знаков в системе (2) при x = a, 
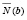– верхнее число перемен знаков в этой системе (
).
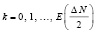Предполагается, что каждый корень полинома (1) считается столько раз, какова его кратность. Если производные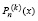 
(k = 1, 2, …, n) не обращаются в нуль при x = a и x = b, то подсчет знаков упрощается, а именно ΔN = N(a) – N(b).
Приведенные утверждения априори не предназначались для компьютерной реализации. В них не определяется местоположение промежутка [a, b] для подсчета всех корней без пропуска. В вычислительной практике могут возникать неточности в случае плохой отделенности корней, особенно в сочетании с большим разбросом их расположения. Неизбежно накопление погрешности при возмущениях коэффициентов. Очевидны сложности при высокой степени полинома. Эти методы необходимо требуют явного задания коэффициентов полинома, тогда как полином может задаваться неявно или своими значениями. В общем случае приведенные методы не совмещаются с одновременным вычислением всех корней. Вследствие необходимости явных коэффициентов полиномов рассматриваемые утверждения непосредственно не переносятся на случаи аналитических функций и трансцендентных уравнений. Оценки области корней полинома – традиционная тема исследований [5; 6]. Исследования в данном направлении активно продолжаются в настоящее время [7; 8]. Большей частью публикуемые оценки имеют аналитический характер и выполняются в аспекте прикладной математики [8; 9]. Наряду с этим исследования области корней полинома проводятся в различных аспектах фундаментальной математики [7; 10, с. 22]. На предмет компьютерной реализации сохраняются отмеченные сложности.
На основании изложенного возникает задача разработать компьютерный метод определения области корней полинома, структуры их расположения, совмещающий локализацию с одновременным вычислением всех корней полинома, который позволял бы находить корни, исключая отмеченные сложности. Требуется, чтобы искомый метод можно было применять также к аналитическим функциям и трансцендентным уравнениям. Предлагаемое решение опирается на алгоритмы устойчивых адресных сортировок.
Цель исследования – в работе требуется дать описание и выполнить обоснование метода программной идентификации области действительных корней полинома, ее структуры и самих корней с помощью сортировки, показать применимость метода для идентификации всех действительных корней аналитических функций и трансцендентных уравнений.
Материалы и методы исследования
Исследование опирается на синтез и анализ алгоритмов сортировки, на методы вычисления корней полиномов в линейной алгебре, на методы поиска корней аналитических функций в математическом анализе, на численное моделирование и программные эксперименты.
Результаты исследования и их обсуждение
Предложен компьютерный метод определения области действительных корней полиномов, который указывает не только границы области корней, но определяет структуру расположения корней и совмещается с вычислением самих корней. Метод реализуется программой стандартного вида, которая не использует математических преобразований полиномов, использует только входные значения модулей полиномов на каждом шаге дискретизации, в дальнейшем – их сравнения, что позволяет достигать высокой точности определения корней. Метод без изменения переносится на идентификацию области и действительных корней любой аналитической функции. Кроме того, метод применим к поиску действительных корней неаналитических функций и трансцендентных уравнений. В реализующей метод программе меняется только подпрограмма, задающая входную функцию, и, кроме того, меняются числовые параметры – начальные произвольно расширенные границы области корней и варьируемый радиус локализации одновременно каждого из корней. К недостаткам метода относится то, что корни полинома (функции) идентифицируются без учета кратности. В случае полинома кратность корня можно определить его непосредственной подстановкой в производные полинома последовательных порядков. Численный эксперимент показывает достоверность работы реализующей метод программы на множестве функций и параметрически заданных границ области их действительных корней. Нарушения точности связаны с выходом из границ числового диапазона.
Программная идентификация области действительных корней полинома и структуры их расположения. Излагаемый метод представляет собой дискретизированный спуск к области всех действительных корней, к локальной окрестности каждого корня и его идентификации без вычислительных преобразований, исключительно с помощью сравнений значений модуля полинома (функции) на каждом последовательном шаге. Метод опирается на принцип минимума модуля [11, с. 198].
Теорема Шварца [11, с. 198]. Если функция f голоморфна в области D и не обращается в нуль в этой области, то | f | может достигать локального минимума внутри D лишь в случае f = const.
Отсюда следует, что локальные минимумы модуля аналитической функции, отличной от константы, могут достигаться только в тех точках, где она обращается в ноль.
Предлагаемый метод находит границы области корней как минимумы модуля полинома (аналитической функции) на основе того факта, что вне области корней такие минимумы исключены. Собственно локальный минимум (точнее, наименьшее значение в дискретизированной локальной окрестности) любой числовой последовательности при помощи устойчивой адресной сортировки всегда находится, причем с единственностью, следующим образом. Для краткости описания выбрана устойчивая адресная сортировка подсчетом по матрице сравнений. Сортировка выполняется по не убыванию, ее описание заимствуется из [12, с. 81]. Пусть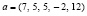 
. Матрица сравнений примет вид
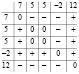
Номер j-го элемента входного массива a в отсортированном массиве c подсчитывается как число нулей и плюсов в j-м столбце матрицы над диагональю, включая диагональный элемент, сложенное с числом плюсов под диагональю (нумерация от j = 1).
Так,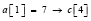 
, 
, 
,
, 
.
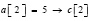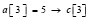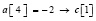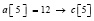Сортировка сохраняет порядок равных элементов (за счет добавления нуля над диагональю на пересечении столбца текущего элемента и строки предшествующего ему равного элемента). Все адреса вставки имеют единственное значение. В программе (Delphi) реализуется взаимно однозначная прямая и обратная адресация:
for j: = 1 to n do
begin
k: = 0; for i: = 1 to j do if a[j]> = a[i] then k: = k+1; for i: = j+1 to n do if a[j]>a[i] then k: = k+1;
c[k]: = a[j]; e[k]: = j;
end;
Каждому входному элементу с индексом j единственным образом ставится в соответствие значение его индекса k в отсортированном массиве: c[k]: = a[j]; Обратно, каждому элементу в отсортированном массиве с индексом k единственным образом ставится в соответствие значение его индекса j во входном массиве: e[k]: = j;
Отсюда элементарно указывается значение индекса локально минимального элемента входного массива. Условие локализации искомого минимума имеет вид
{выполнение процедуры сортировки sort}
k: = 1; while k < = n do begin for L: = 1 to k-1 do if abs(e[k]-e[k-L]) < = eps0 then goto 11; ik: = e[k];
11: k: = k+1 end;
Здесь ik – индекс локально минимального элемента в окрестности радиуса eps0. Оператор ik: = e[k]; выполняется, если входной индекс e[k-L] любого элемента меньшего c[k] (a[e[k]]) располагается от e[k] дальше, чем на eps0. Иными словами, индекс элемента меньшего локализуемого не должен попасть в окрестность индекса локально минимального элемента. На вход сортировки с шагом дискретизации h, как элементы массива, поступают значения модуля полинома. В результате выполнения данного условия в окрестности радиуса eps0 окажется один и только один корень в некотором приближении. К нему выполняется спуск посредством итеративного сужения диаметра окрестности локализованного приближения – до сближения концов диаметра меньше априори заданной границы абсолютной погрешности. Метод в целом детально описан в [12]. Там же, в примере 3, приводится программная реализация поиска корней на основе изложенной сортировки [12, с. 85] и результаты численного эксперимента. Данную сортировку можно заменить на более быструю сортировку слиянием по матрицам сравнений, имеющую временную сложность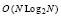 
. Такая сортировка также сохраняет устойчивость (порядок равных элементов) и взаимно однозначное соответствие входных и выходных индексов. На выходе эта сортировка, как и описанная выше, в порядке возрастания формирует отсортированный массив c и массив входных индексов e, элементы которого располагаются в порядке отсортированных элементов (аналогично сортировке подсчетом: c[k]: = a[j]; e[k]: = j;). Однако входной и выходной массивы совмещаются в один переменный массив c, что не препятствует применению описанного выше условия локализации минимального элемента через индексы массива e. Ее полное описание приводится, в частности, в [13, с. 86].
Программа реализации поиска корней на основе сортировки слиянием заимствуется из [12, с. 91] с существенными изменениями входных параметров. Полностью программу непосредственно ниже представляет пример 1. Данная программа является базовой для излагаемого компьютерного метода идентификации корней полиномов и функций. Все 11 приводимых ниже примеров численного эксперимента выполнены на основе именно этой программы с соответственными изменениями параметров. Изменения конкретно приводятся в каждом примере численного эксперимента.
Пример 1. Идентификацию всех действительных корней полинома 60-й степени реализует следующая программа на основе устойчивой адресной сортировки слиянием (в разделе констант программы сортировка задается процедурой sort):
program KORDEMINPOLsortnewprost;
{$APPTYPE CONSOLE}
uses
SysUtils;
label 21, 22; const n1 = 60;
b: array [1..n1] of extended = (-51.0007, -51.0006,-1.01, -2.02, -3.03, -4.0007, -4.0008, -5.05, -6.0001,
-6.0002, -7.07, -8.08, -9.09, -10.01, -11.011, -12.012, -13.013,-14.014, -15.015, -16.016, -17.017, -18.018,
-19.0003, -19.0002, -20.02, -21.021, -22.022, -23, -23.023, -23.0231,1, 2, 3, 4.0007, 4.0008, 5, 6.0001,
6.0002, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19.0003, 19.0002, 20, 21, 22, 23,
23.023, 23.0231, 61.0005, 61.0006);
eps = 1E-44; eps0 = 0.000049; h = eps0/33; n00 = 1512; mm = 4; x00 = -65; x11 = 65;
type vect1 = array [0..4*n00] of extended; vect2 = array [0..4*n00] of longint;
vec = array [0..n1] of extended;
var i,j,k,l,ee,nn0: longint; a,c: vect1; e: vect2; b1:vec;
aaa,x,x0,x1,xk,xk0,xk1,h0,min,eps1,hh,z,z1: extended;
function func (var x: extended): extended;
var i1: 1..n1;p:extended;
begin p: = 1; for i1: = 1 to n1 do p: = p*(x-b1[i1]); func: = abs(p); end;
procedure min1 (var x: extended;var ee:longint);
begin min: = func(x); ee: = 0; for i: = 1 to mm do begin
x: = xk0+i*h0; if min > func(x) then begin min: = func(x); ee: = i; end;end;end;
procedure sort (var nn0:longint; var c: vect1; var e: vect2);
type vecc = array[0..4*n00] of longint;
var ab:integer; i,j,k,l,m,r,nm,p,n: longint; e1, e2: vecc;
begin
p : = trunc(ln(nn0)/ln(2)); if p<> ln(nn0)/ln(2) then p : = p+1;
n : = round(exp(p*ln(2)));
for l : = 1 to n do if l< = nn0 then e[l] : = l else ab: = 1;
for r : = 1 to p do begin m : = round(exp(r*ln(2))); nm: = n div m;
for k : = 0 to nm-1 do begin
for l : = 1 to m div 2 do begin
if (k * m + l > nn0) or (e[k * m + l]>nn0) then ab : = l
else e1[l] : = e[k * m + l];
if (k * m + m div 2+ l > nn0) or (e[k * m + m div 2+ l]>nn0) then ab : = 1
else e2[l] : = e[k * m + m div 2 + l] end;
i : = 1; j : = 0; while i + j < = m do begin
if i = m div 2 + 1 then ab : = -1;
if j = m div 2 then ab : = 1;
if (k * m + i > nn0) or (e[k * m + i]>nn0)
or (k * m + m div 2 + j > nn0-1) or (e[k * m + m div 2+ j]>nn0)
then ab: = 1;
if (i < = m div 2) and (j < = m div 2 -1) and (k * m + i< = nn0)
and (k * m + m div 2 + j < = nn0-1)
then if (e2[j + 1] > nn0) or (e1[i]> nn0) then ab : = 1 else
begin if c[e2[j + 1]] – c[e1[i]] = 0 then ab : = 0; if c[e2[j + 1]] – c[e1[i]]> 0 then ab : = 1;
if c[e2[j + 1]] – c[e1[i]]< 0 then ab : = -1 end; if ab > = 0 then
begin e[k * m + i + j] : = e1[i]; i : = i + 1 end else begin e[k * m + i + j] : = e2[j + 1]; j : = j + 1 end
end end end end;
begin
aaa: = 1e62; nn0: = n00; hh: = nn0*h;
x0: = x00; for i: = 1 to n1 do b1[i]: = b[i]; while x0 < = x11 do
begin for i: = 1 to nn0 do begin x: = x0+i*h; c[i]: = func(x); end;
sort(nn0, c, e); k: = 1; while k< = nn0 do
begin for l : = 1 to k-1 do if abs(e[k]-e[k-l]) < = eps0/h then goto 22;
xk: = x0+e[k]*h; eps1: = eps0; xk0: = xk-eps1; xk1: = xk+eps1; h0: = abs(2*eps1)/mm;
while abs(eps1) > eps do begin x: = xk0; min1(x,ee); eps1: = eps1/1.2;
xk0: = xk0+ee*h0-eps1; xk1: = xk0+ee*h0+eps1; h0: = abs(2*eps1)/mm; end;
if func(xk) = 0 then begin x: = xk; goto 21; end;
x: = xk0+ee*h0+eps1;
for i: = 1 to 2 do begin z: = x+i*h; if func(x) > = func(z) then goto 22; end;
for i: = 1 to 2 do begin z1: = x-i*h; if func(x) > = func(z1) then goto 22; end;
if abs(aaa-x)< = 1e-20 then goto 22;
21: writeln (‘ ‘, x,’ ‘,func(x)); aaa: = x;
22: k: = k+1 end; x0: = x0 + hh end;
readln;
end.
Модуль полинома в этой программе задает подпрограмма-функция вида
function func (var x: extended): extended;
var i1: 1..n1;p:extended;
begin p: = 1; for i1: = 1 to n1 do p: = p*(x-b1[i1]); func: = abs(p); end;
Полином вычисляется по формуле
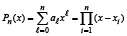, (3)
где предполагается, что an = 1. В (3) и ниже коэффициенты полинома, в отличие от (1), нумеруются по возрастанию степеней. Для тестовой проверки корни на входе программы задаются в разделе констант как массив b: array [1..n1] of extended из 60 элементов. Такой прием будет использоваться в дальнейшем, однако он не является необходимым, и способ задания модуля полинома (функции) по ходу исследования будет меняться. Данная программа непосредственно находит все 60 действительных корней полинома 60-й степени на отрезке [x00, x11] (x00 = -65; x11 = 65;) без искажения мантиссы корня с точностью до представления чисел с плавающей точкой в формате extended языка программирования:
-5.10007000000000E+0001 0.00000000000000E+0000
-5.10006000000000E+0001 0.00000000000000E+0000
-2.30231000000000E+0001 0.00000000000000E+0000
-2.30230000000000E+0001 0.00000000000000E+0000
-2.30000000000000E+0001 0.00000000000000E+0000
-2.20220000000000E+0001 0.00000000000000E+0000
-2.10210000000000E+0001 0.00000000000000E+0000
-2.00200000000000E+0001 0.00000000000000E+0000
-1.90003000000000E+0001 0.00000000000000E+0000
-1.90002000000000E+0001 0.00000000000000E+0000
……..……………………………………………………..
4.00070000000000E+0000 0.00000000000000E+0000
4.00080000000000E+0000 0.00000000000000E+0000
5.00000000000000E+0000 0.00000000000000E+0000
6.00010000000000E+0000 0.00000000000000E+0000
6.00020000000000E+0000 0.00000000000000E+0000
…………………….……………………………………..
1.90002000000000E+0001 0.00000000000000E+0000
1.90003000000000E+0001 0.00000000000000E+0000
2.00000000000000E+0001 0.00000000000000E+0000
……………………….…………………………………..
2.30230000000000E+0001 0.00000000000000E+0000
2.30231000000000E+0001 0.00000000000000E+0000
6.10006000000000E+0001 0.00000000000000E+0000
6.10005000000000E+0001 0.00000000000000E+0000
В левой колонке – корни полинома, в правой – значения в них модуля полинома. Некоторые корни теста априори взаимно отличались на 0.0001 и располагались с разбросом.
Предложение 1. Нулевые значения полинома получаются соответственно определению корня, обращающего полином в нуль. Точность идентификации корней и значений полинома достигается за счет того, что программа не использует числовые преобразования, но только сравнивает дискретные числовые значения на всем протяжении ее выполнения, чем исключается накопление погрешности.
Исполнительную часть программы иллюстрирует блок-схема:
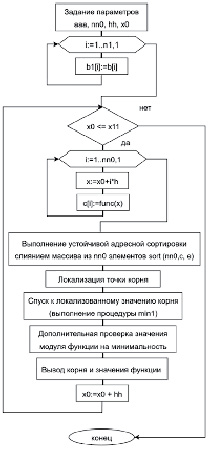
Рис. 1. Блок-схема раздела инструкций программы KORDEMINPOLsortnewprost Источник: составлено авторами
Непосредственно ниже иллюстрируется блок локализации корня полинома (функции).
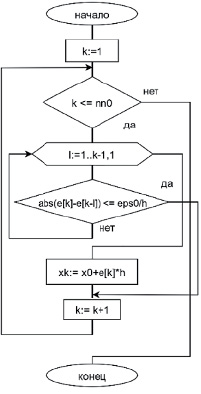
Рис. 2. Блок-схема локализации точки корня Источник: составлено авторами
К локализованному приближению корня выполняется спуск по алгоритму выбора наименьшего значения модуля функции, дискретизированной на равномерной сетке из mm элементов в локализованной окрестности, и последующего циклического сужения границ окрестности до достижения априори заданной точности приближения к корню.
Все используемые на рис. 1–3 программные фрагменты представлены в программе примера 1 и детализируются в дальнейшем.
Данный эксперимент можно существенно усилить [13]. Для дальнейшего наиболее принципиально то, что приведенный результат совершенно не изменится, если корни данного полинома искать на произвольно расширенном промежутке. Чтобы в этом убедиться, можно взять, не меняя других параметров, например, отрезок x00 = -300; x11 = 300. Возрастет время выполнения программы. Сам же результат не изменится потому, что вне области корней по теореме Шварца минимумов модуля полинома не существует, и программа вне области корней никаких минимумов модуля не идентифицирует.
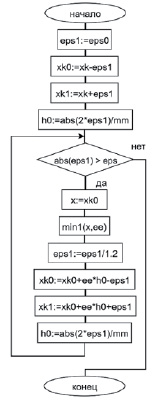
Рис. 3. Блок-схема алгоритма спуска от локализованного к точному значению корня Источник: составлено авторами
Предложение 2. Идентифицировать минимумы модуля полинома программа начнет, только подойдя к области расположения корней, за счет того, что в области будут достигаться значения модуля полинома сравнительно близкие к нулю, соответственно меньшие, чем вне области корней. При этом, при любом задании радиуса окрестности локализации, программа, локализовав корень, выполняет к нему спуск путем сужения границ локализованной окрестности до достижения априори заданной точности приближения к корню (рис. 1–3). Только после полной его идентификации программа переходит к поиску локальной окрестности другого корня.
Локализация минимума модуля полинома в данном примере программы происходит в радиусе eps0 = 0.000049. Эта величина по смыслу условия локализации всегда должна быть меньше половины расстояния между ближайшими друг к другу корнями (точками минимумов модуля полинома; в данном примере – меньше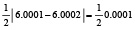 
).
При любом дальнейшем уменьшении радиуса локализации программа будет получать тот же правильный результат. При увеличении – может потерять соседние локальные минимумы. Согласно численному эксперименту шаг дискретизации надежно сохраняет устойчивость программы, если он не больше h = eps0/33. Любое уменьшение шага сохраняет правильный результат. Увеличение шага может привести к потерям корней и вычислительным ошибкам (за счет заведомой потери значащих цифр или самих входных данных).
При правильном задании входных параметров программа сама определит область корней и найдет все корни. Однако сложность в том, что при уменьшении радиуса локализации программа замедляется. Она замедляется также при сохранении радиуса локализации, но с ростом промежутка, ограничивающего область корней полинома. В общем случае границы области корней неизвестны, поэтому их начальные приближения требуется брать с большим запасом, чтобы они заведомо включали всю искомую область корней. Если в данном примере без изменения других параметров взять границы x00 = -300000; x11 = 300000, программа попадет в область корней и найдет их с той же точностью, но это займет значительное время. Выход подсказывает следующая особенность. При условии, что программа работает в границах, включающих область всех корней, она при любом выборе радиуса локализации, меньшего половины размера области корней, локализует (рис. 2) и идентифицирует (рис. 3) хотя бы один корень. Это произойдет потому, что вне области корней она не идентифицирует минимума модуля полинома, а внутри области по построению получит наименьшее значение в радиусе меньшем половины диаметра области корней.
Так, например, если взять границы x00 = -300000; x11 = 300000; и положить eps0 = 0.5; то получится следующий результат работы программы:
-5.10006000000000E+0001 0.00000000000000E+0000
-5.10007000000000E+0001 0.00000000000000E+0000
-6.00020000000000E+0000 0.00000000000000E+0000
-2.30000000000000E+0001 0.00000000000000E+0000
-7.07000000000000E+0000 0.00000000000000E+0000
-9.09000000000000E+0000 0.00000000000000E+0000
-8.08000000000000E+0000 0.00000000000000E+0000
…………………………………………………………..
2.10000000000000E+0001 0.00000000000000E+0000
2.20000000000000E+0001 0.00000000000000E+0000
1.90003000000000E+0001 0.00000000000000E+0000
6.10006000000000E+0001 0.00000000000000E+0000
6.10005000000000E+0001 0.00000000000000E+0000
Курсивом выделены наименьший и наибольший корни. Полезная особенность программы заключается в том, что результат ее работы всегда представляет собой множество (возможно, неполное) точных значений корней (согласно предложению 2). Именно это дает возможность видеть структуру их расположения в случае, когда эти корни разбросаны по области. Структура дополнительно показывает, с каким радиусом локализации следует выполнять окончательное вычисление: в данном примере есть корни взаимно отделенные на 0.0001. Остается отступить от наименьшего и наибольшего корня на некоторое расстояние и взять достаточно малый радиус локализации (с запасом малости, учитывая степень полинома и зная, что все искомые корни действительны), например, eps0 = 0.000049. Таким образом, границы и параметры окончательного вычисления можно задать в виде
eps = 1E-44; eps0 = 0.000049; h = eps0/33; n00 = 1512; mm = 4; x00 = -62; x11 = 62;
в результате получится приведенный вначале полный и правильный результат. Здесь и в дальнейшем eps = 1E-44 означает априори задаваемую границу абсолютной погрешности, достижение которой проверяется при спуске к локализованному значению корня (рис. 3).
Поскольку наглядно проявляется расположение корней, можно разбить вычисление на части в соответственных границах: x00 = -62; x11 = -60; x00 = -24; x11 = 24; x00 = 60; x11 = 62. Это позволит ускорить процесс с сохранением точности посредством пропуска пустых мест.
Замечание 1. Недостаток программы в том, что она вычисляет корни без учета их кратности. Если полином задается в виде
,
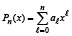то такой недостаток устраняется подстановкой каждого найденного корня в производную полинома
.
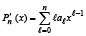В общем случае, если корень полинома Pn(x) имеет кратность k, то он является корнем кратности k–1 производной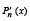 
этого полинома [3, с. 178, 179]. Поэтому кратность корня подсчитывается его подстановкой в последовательные производные до момента обнаружения производной наименьшего порядка k, которую этот корень не обращает в ноль:
.
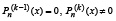Такой корень полинома Pn(x) имеет кратность k.
Модуль полинома в программе можно задавать как модуль полинома с коэффициентами:
.
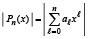Для этого подпрограмма func меняется, как показано в следующем примере.
Пример 2. Пусть взят полином 4-й степени
.
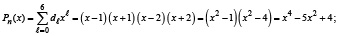
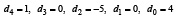Коэффициенты задаются в разделе констант подпрограммы:
function func (var x: extended): extended;
const n1 = 4; d: array [0..n1] of extended = (4,0,-5,0,1); var i1: 0..n1;p:extended;
begin p: = d[n1]; for i1: = 1 to n1 do p: = p*x+d[n1-i1]; func: = abs(p); end;
Здесь значение полинома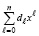 
определяется по схеме Горнера:
.
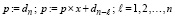Программа KORDEMINPOLsortnewprost, в которой не меняются остальные параметры (массив b задавать излишне), найдет корни:
-2.00000000000000E+0000 0.00000000000000E+0000
-1.00000000000000E+0000 0.00000000000000E+0000
1.00000000000000E+0000 0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
Аналогичный тест любой сложности можно сконструировать на основе алгоритма восстановления коэффициентов полинома по его корням xk, k = 1, 2, …, n, отличного от формул Виета [14, с. 292]:
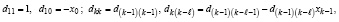
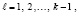
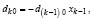k = 1, 2, …, n.
При k = n получится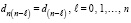 
, и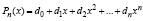 
, где dn = 1.
Коэффициенты можно задать как элементы переменного массива. В этом случае полином может поступать в программу неявно. Оценку Маклорена можно встроить в программу для автоматического задания расширенных границ области.
Замечание 2. Ограничение изложенного подхода состоит в том, что значения полинома (аналогично, аналитической или другого вида функции) на исследуемом промежутке не должны выходить за границы диапазона допустимых значений в языке программирования. Иначе наступает искажение значащих цифр элементов входного массива, что влечет недостоверную оценку области корней и ошибки их вычисления.
Предложение 3. Чтобы совместить программную идентификацию границ области действительных корней полинома с идентификацией самих корней, достаточно оформить программу KORDEMINPOLsortnewprost отдельной процедурой, входными и выходными параметрами которой являются границы области поиска x00, x11 и радиус локализации корней eps0. В разделе инструкций программы обращаться к процедуре следует дважды. Первый раз – с расширенными параметрами x00, x11 и увеличенным радиусом локализации eps0. Среди значений выходных параметров будут наименьший и наибольший из идентифицированных корней в границах области, которые можно принять за новые приближения границ. Данные границы расширяются на константу влево и вправо, после чего принимаются за новые входные параметры той же процедуры вместе с уменьшенным до необходимого значения eps0. Второе обращение к процедуре с новыми параметрами влечет окончательную идентификацию всех действительных корней полинома. В случае необходимости обращение можно итеративно повторять с циклическим уменьшением параметров для уточнения области корней, их расположения и значений.
Изложенный метод является компьютерным, не опирается на аналитические оценки области корней, реализуется программой стандартного вида без математических преобразований. Вычисляются лишь входные значения модуля полинома (в дальнейшем функции) на каждом шаге дискретизации (рис. 1), по ходу программы выполняются только операции сравнения (рис. 1–3), что не влечет накопление погрешности. Используются непосредственно значения полиномов (функций), для их задания не являются необходимыми коэффициенты, значения могут вычисляться неявно. Переменными параметрами являются начальные границы области корней и радиус локализации одновременно каждого из корней. Идентификация границ области корней может совмещаться с идентификацией самих корней. Согласно эксперименту, как правило, все корни идентифицируются без пропуска, с точностью до представления числовых данных в формате extended.
Замечание 3. Формально метод не является точным (прямым), поскольку зависит от начальных данных, параметров и априори заданной границы погрешности приближения. Кроме того, можно привести примеры, когда на практике точность идентификации нарушается, что, как правило, обусловлено выходом из границ числового диапазона языка программирования.
Программная идентификация области и значений действительных корней аналитической функции. Теорема Шварца применима к любой аналитической функции, поэтому изложенные рассуждения, с точностью до стилистических оговорок, сохраняются при замене термина «полином» термином «аналитическая функция». Вне области корней аналитическая функция в ноль не обращается, к такой функции можно применить оценку границ и расположения корней с помощью программы KORDEMINPOLsortnewprost. Замечание 3 в этом случае особо существенно. Так, экспонента от полинома может выходить за границы диапазона уже при сравнительно небольших значениях независимой переменной и высокой степени полинома.
Чтобы применить метод, достаточно модуль аналитической функции в программе определить с помощью подпрограммы func. Определять массив корней b при этом нет необходимости, однако в тестовых примерах этим массивом можно пользоваться.
Замечание 4. Необходимо проверять корректность представления функции в языке программирования. Для сложной суперпозиции замедляется время работы программы, поскольку суперпозиция вычисляется на каждом дискретном шаге на входе, при выполнении спуска и на выходе программы.
Пример 3. Пусть рассматривается функция
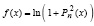, (4)
где Pn(x) – полином из (3). Чтобы программа KORDEMINPOLsortnewprost идентифицировала границы области корней и корни этой функции, в подпрограмме func надо задать модуль именно функции (4). В случае использования массива тестовых элементов b из программы примера 1 для задания полинома подпрограмма func примет вид
function func (var x: extended): extended;
var i1: 1..n1;p:extended;
begin p: = 1; for i1: = 1 to n1 do p: = p*(x-b[i1]); func: = abs(ln(1+sqr(p))); end.
Если действовать по той же схеме, которая описана выше для полинома, и в границах x00 = -300000; x11 = 300000; взять сравнительно большой радиус локализации eps0 = 0.5; то без изменения других параметров и элементов массива b результат работы программы
-5.10006000000000E+0001 0.00000000000000E+0000
-5.10007000000000E+0001 0.00000000000000E+0000
-6.00020000000000E+0000 0.00000000000000E+0000
-2.30000000000000E+0001 0.00000000000000E+0000
………………………………………………..………….
2.20000000000000E+0001 0.00000000000000E+0000
1.90003000000000E+0001 0.00000000000000E+0000
6.10006000000000E+0001 0.00000000000000E+0000
6.10005000000000E+0001 0.00000000000000E+0000
появится практически без задержки. Из распечатки видно, что корни находятся между -51.0007 и 61.0006. Отсюда идентифицировать их без пропуска и без ошибок в границах x00 = -62; x11 = 62 с радиусом локализации eps0 = 0.000049 удается за сравнительно короткое время. Результат идентификации полностью совпадет с тем, который приводился для этих параметров в случае полинома Pn(x) в примере 1, – все корни функции (4) с одинаковой точностью совпадут с корнями полинома 60-й степени Pn(x), задававшимися тестовым массивом b: array [1..n1] of extended из 60 элементов. Их повторная распечатка здесь была бы излишней.
Полином, входящий в суперпозицию, в рассматриваемой программе можно задавать как полином с коэффициентами:
.
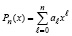Пример 4. Пусть дана функция
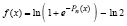, (5)
где n = 6 и
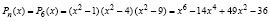. (6)
Для применения схемы Горнера в подпрограмме func коэффициенты задаются в обратном порядке: const n1 = 6; d: array [0..n1] of extended = (-36,0,49,0,-14,0,1). Подпрограмма примет вид
function func (var x: extended): extended;
const n1 = 6;
d: array [0..n1] of extended = (-36,0,49,0,-14,0,1);
var i1: 0..n1;p:extended;
begin
p: = d[n1]; for i1: = 1 to n1 do p: = p*x+d[n1-i1]; func: = abs(ln(1+exp(-p))-ln(2));
end.
При данном видоизменении и при параметрах
eps = 1E-44; eps0 = 0.000049; h = eps0/33; n00 = 1512; mm = 4; x00 = -70; x11 = 70;
для функции (5), (6) получится результат работы программы:
-3.00000000000000E+0000 0.00000000000000E+0000
-2.00000000000000E+0000 0.00000000000000E+0000
-1.00000000000000E+0000 0.00000000000000E+0000
1.00000000000000E+0000 0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
3.00000000000000E+0000 0.00000000000000E+0000
Если по предложенной схеме вначале искать границы области корней функции (5), (6), то надо взять параметры
eps = 1E-44; eps0 = 0.5; h = eps0/33; n00 = 1512; mm = 4; x00 = -300000; x11 = 300000; (7)
Однако при этих параметрах программа выдаст тот же результат, поскольку корни взаимно отделены не менее чем на единицу.
Пример 5. Пусть рассматривается функция, включающая гауссиан:
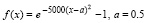. (8)
Подпрограмма func непосредственно задается в виде
function func (var x: extended): extended;
begin func: = abs(exp(-5000*sqr(x-0.5))-1) end.
С этим изменением и изменением границ параметров (7) x00 = -30; x11 = 30; программа KORDEMINPOLsortnewprost даст следующий результат поиска корня функции (8):
5.00000000000000E-0001 0.00000000000000E+0000.
К сожалению, такая точность не сохраняется в границах параметров (7). Она не сохраняется также при замене значения а в (8). Так, при a = 0.3 получится
2.99999999997672E-0001 0.00000000000000E+0000.
Это объясняется потерей значащих цифр в процессе вычисления значения функции (8) вследствие нарушения числового диапазона.
Пример 6. Пусть рассматривается функция
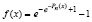, (9)
где Pn(x) из (6).
Подпрограмма func записывается в виде
function func (var x: extended): extended;
const n1 = 6;
d: array [0..n1] of extended = (-36,0,49,0,-14,0,1);
var i1: 0..n1;p:extended;
begin p: = d[n1]; for i1: = 1 to n1 do p: = p*x+d[n1-i1]; func: = abs(exp (-exp(-p)+1)-1); end.
При параметрах (7), где для иллюстрации метода радиус локализации заменяется на eps0 = 1; программа KORDEMINPOLsortnewprost выдает следующие элементы области корней
-1.00000000000000E+0000 0.00000000000000E+0000
1.00000000000000E+0000 0.00000000000000E+0000
С учетом радиуса локализации (диаметр окрестности равен 2) можно допустить, что область корней включает промежуток [–3, 3] (на величину 2*eps0 можно отступить влево и вправо от наименьшего и наибольшего корня). Естественно этот промежуток увеличить – масштаб границ, в которых он найден, позволяет это выполнить, например, так: x00 = -10; x11 = 10; окончательный радиус локализации можно взять с запасом: eps0 = 0.000049. С указанной выше подпрограммой func и с выбранными параметрами программа KORDEMINPOLsortnewprost даст правильный результат. Впрочем, вследствие эталонной отделенности корней, эта программа сразу даст правильный результат и при параметрах (7):
-1.00000000000000E+0000 0.00000000000000E+0000
1.00000000000000E+0000 0.00000000000000E+0000
-2.00000000000000E+0000 0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
3.00000000000000E+0000 0.00000000000000E+0000
-3.00000000000000E+0000 0.00000000000000E+0000
Пример 7. Пусть снова рассматривается функция (9), но полином Pn(x) в показателе степени образован как произведение биномов из 10 корней, некоторые из них взаимно отделены на 0.0001:
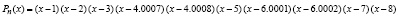. (10)
Включение в программу KORDEMINPOLsortnewprost тестовых значений из (10) можно выполнить с помощью массива b: array [1..n1] of extended. Соответственно, программа должна включать следующие изменения. В разделе констант –
const n1 = 10; b: array [1..n1] of extended = (1, 2, 3, 4.0007, 4.0008, 5, 6.0001, 6.0002, 7, 8);
и подпрограмма func примет вид
function func (var x: extended): extended;
var i1: 1..n1;p:extended;
begin p: = 1; for i1: = 1 to n1 do p: = p*(x-b[i1]); func: = abs(exp(-exp(-p)+1)-1); end.
Если теперь искать область корней функции (9) с полиномом (10) в показателе, то можно выбрать параметры (7). Без каких-либо других изменений программа выдаст результат:
5.00000000000000E+0000 0.00000000000000E+0000
3.00000000000000E+0000 0.00000000000000E+0000
7.00000000000000E+0000 0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
8.00000000000000E+0000 0.00000000000000E+0000
1.00000000000000E+0000 0.00000000000000E+0000
6.00020000000000E+0000 0.00000000000000E+0000
4.00080000000000E+0000 0.00000000000000E+0000
Результат дает примерные границы области корней, [1, 8], а также информацию о структуре – корни включают десятичные мантиссы 0.0001 и 0.0008. С учетом радиуса локализации границы можно раздвинуть на единицу влево и вправо, что влечет [0, 9]. Промежуток можно увеличить, взяв, например, [–5, 20]. Радиус локализации можно взять достаточно малым: eps0 = 0.000049; Окончательные параметры примут вид
eps = 1E-44; eps0 = 0.000049; h = eps0/33; n00 = 1512; mm = 4; x00 = -5; x11 = 20.
Результат работы программы:
1.00000000000000E+0000 0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
3.00000000000000E+0000 0.00000000000000E+0000
4.00070000000000E+0000 0.00000000000000E+0000
4.00080000000000E+0000 0.00000000000000E+0000
5.00000000000000E+0000 0.00000000000000E+0000
6.00020000000000E+0000 0.00000000000000E+0000
6.00010000000000E+0000 0.00000000000000E+0000
7.00000000000000E+0000 0.00000000000000E+0000
8.00000000000000E+0000 0.00000000000000E+0000
Все корни идентифицированы без пропуска и без искажения значащих цифр мантиссы.
Замечание 5. Функция (9) включает суперпозицию экспонент. Эти быстро растущие функции, если не ограничивать диапазона переменной и их значений, выходят из числового диапазона компьютера, что приводит к отказу его работы вследствие переполнения. Поэтому степень полинома в показателе требует ограничения и требует ограничения диапазон изменения независимой переменной. Так, если вместо (10) в качестве полинома взять полином 11-й степени с добавлением только одного корня
const n1 = 11; b: array [1..n1] of extended = (1, 2, 3, 4.0007, 4.0008, 5, 6.0001, 6.0002, 7, 8, 9),
то в рассмотренном диапазоне примера 7 наступит переполнение.
В итоге относительно идентификации области корней аналитической функции можно отметить следующее.
Предложение 4. Вне области корней аналитическая функция не обращается в ноль в силу второй теоремы Шварца, и к такой функции можно применить оценку границ и структуры расположения корней с помощью программы KORDEMINPOLsortnewprost. Единственное изменение в этой программе по сравнению с вычислением корней полинома включает подпрограмма func, которая теперь задает не полином, а конкретную аналитическую функцию. При этом необходимо принять во внимание отмеченные ограничения на диапазоны аргументов и значений функции. В рамках данных ограничений сохраняется инвариантность компьютерного метода и точность идентификации границ области, а также самих корней аналитической функции. Чтобы совместить программную идентификацию границ области действительных корней полинома с идентификацией самих корней, следует применить аналог итерационной схемы, описанной в предложении 3.
Относительно классификации метода сохраняется замечание 3.
Программная идентификация области и значений действительных корней трансцендентных уравнений. Наименьшее значение в окрестности элемента любой числовой последовательности по условию локализации всегда находится с единственностью [12]. Отсюда изложенная идентификация границ области корней аналитической функции применима к неаналитическим функциям с простым видоизменением. Именно, достаточно использовать программное условие, исключающее из рассмотрения аргументы функции, в которых ее значение отделено от нуля больше, чем на априори заданный числовой порог. Так, в программе KORDEMINPOLsortnewprost после метки 21: можно поставить оператор if … then с требуемой границей. Например,
21: if func(x)< = 1e-20 then writeln (‘ ‘, x,’ ‘,func(x),’ ‘,x/pi,’ ‘,round(x/pi),’ ‘); aaa: = x. (11)
Пример 8. Пусть рассматривается неаналитическая функция
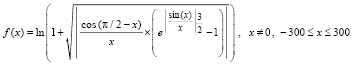. (12)
Функция (12) задается в подпрограмме func с условием, исключающим деление на ноль:
function func (var x: extended): extended;
begin if x<>0 then func: = abs(ln(1+sqrt(abs(cos(pi/2-x)/x*(exp(sqrt(abs(1/x*sin(x)))*abs(1/x*sin(x)))-1))))); end.
В условии вывода (11), помимо указанного ограничения на допустимые значения функции константой 10–20, используются оператор вывода значений x/pi и round(x/pi). Они показывают связь выводимых значений с числом π с целью тестового контроля найденных корней. С отмеченными изменениями и при параметрах
eps = 1E-44; eps0 = 0.00049; h = eps0/33; n00 = 1512; mm = 4; x00 = -300; x11 = 300;
программа KORDEMINPOLsortnewprost даст результаты идентификации корней:
-2.98451302091073E+0002 0.00000000000000E+0000 -9.50000000000136E+0001 -95
-2.95309709437483E+0002 0.00000000000000E+0000 -9.40000000000135E+0001 -94
-2.92168116783893E+0002 0.00000000000000E+0000 -9.30000000000133E+0001 -93
-2.89026524130302E+0002 0.00000000000000E+0000 -9.20000000000132E+0001 -92
……………………………………………………………………………………………….
-6.28318530718049E+0000 0.00000000000000E+0000 -2.00000000000029E+0000 -2
-3.14159265359024E+0000 0.00000000000000E+0000 -1.00000000000014E+0000 -1
3.14159265358934E+0000 0.00000000000000E+0000 9.99999999999857E-0001 1
6.28318530717869E+0000 0.00000000000000E+0000 1.99999999999971E+0000 2
……………………………………………………………………………………………….
2.89026524130220E+0002 0.00000000000000E+0000 9.19999999999868E+0001 92
2.92168116783809E+0002 0.00000000000000E+0000 9.29999999999867E+0001 93
2.95309709437398E+0002 0.00000000000000E+0000 9.39999999999865E+0001 94
2.98451302090988E+0002 0.00000000000000E+0000 9.49999999999864E+0001 95
Все корни функции (12) на промежутке [–300, 300] найдены без пропуска с 10 верными значащими цифрами десятичной мантиссы в представлении чисел с плавающей точкой. Точность ниже, чем в предыдущих примерах, объясняется машинной погрешностью вычисления суперпозиции стандартных функций. Вследствие хорошей отделенности корней с радиусом локализации eps0 = 0.00049 сразу получились все корни в заданной области, так что область корней определилась непосредственно со всеми их значениями. Совершенно такой же результат (без улучшения точности и без изменения значащих цифр корней) получится, если взять eps0 = 0.000049. В силу периодичности расположения корней аналогичный результат получался бы в произвольно заданной области допустимых значений функции (12). В частности, на промежутке [–300000, 300000] все корни были бы найдены без пропуска и без изменения точности. В правильности нахождения корней можно непосредственно убедиться, сопоставив их с видом рассматриваемой функции: все корни кратны числу π и их номера не содержат пропуска, при этом нулевое значение корня исключено из области допустимых значений по условию вывода.
Для решения трансцендентного уравнения
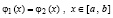, (13)
где обе функции такие, что обосновано существование на данном промежутке корня их разности, на вход программы достаточно подавать функцию
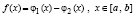. (14)
В подпрограмме func осуществляется переход к модулю этой функции. Тогда программа KORDEMINPOLsortnewprost с описываемыми ниже изменениями даст приближения всех искомых корней уравнения (13).
Пример 9. Пусть рассматривается уравнение (13) вида
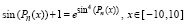, (15)
где Pn(x) из (10). В соответствии с (14) применительно к (15) и с учетом (10) подпрограмма func примет вид
function func (var x: extended): extended;
var i1: 0..n1;p:extended;
begin
p: = 1; for i1: = 1 to n1 do p: = p*(x-b[i1]);
func: = abs(sin(P)+1-exp(sqr(sqr(sin(P)))));
end;
В остальном программа не отличается от предыдущей (выходные корни не индексируются). В таком виде при eps0 = 0.0049 программа позволит определить примерные границы области из следующего множества корней:
3.00000000000000E+0000 0.00000000000000E+0000
4.00080000000000E+0000 0.00000000000000E+0000
5.00000000000000E+0000 0.00000000000000E+0000
6.00010000000000E+0000 0.00000000000000E+0000
Эту область можно расширить от наименьшего и наибольшего из корней с запасом, например, x00 = -1; x11 = 10.
Замечание 6. При поиске корней трансцендентных уравнений ограничение на величину модуля выводимой функции в виде (11), но без специфики тригонометрической индексации корней, 21: if func(x)< = 1e-20 then writeln (‘ ‘, x,’ ‘,func(x), ‘ ‘); aaa: = x; является всегда необходимым. Кроме того, вследствие вычисления входных значений сложных суперпозиций для идентификации корней часто необходимо брать радиус локализации на порядок меньший половины расстояния между ближайшими корнями.
Так, в данном примере для уравнения (15) при eps0 = 0.0000049; получится
1.00000000000000E+0000 0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
3.00000000000000E+0000 0.00000000000000E+0000
4.00070000000000E+0000 0.00000000000000E+0000
4.00080000000000E+0000 0.00000000000000E+0000
5.00000000000000E+0000 0.00000000000000E+0000
6.00020000000000E+0000 0.00000000000000E+0000
6.00010000000000E+0000 0.00000000000000E+0000
7.00000000000000E+0000 0.00000000000000E+0000
8.00000000000000E+0000 0.00000000000000E+0000
При eps0 = 0.000049 программа пропускала один корень, что не соответствовало степени полинома (10), входящего в уравнение (15).
Пример 10. Пусть рассматривается уравнение (15), где полином (10) меняется на полином (6). Соответственно, (14), (15) с учетом (6) подпрограмма func примет вид
function func (var x: extended): extended;
const n1 = 6;
d: array [0..n1] of extended = (-36,0,49,0,-14,0,1);
var i1: 0..n1;p:extended;
begin
p: = d[n1]; for i1: = 1 to n1 do p: = p*x+d[n1-i1];
func: = abs(sin(P)+1-exp(sqr(sqr(sin(P)))));
end.
При eps0 = 0.0049 результат работы программы покажет структуру области корней:
-3.00000000000000E+0000 0.00000000000000E+0000
-2.00000000000000E+0000 0.00000000000000E+0000
-1.00000000000000E+0000 0.00000000000000E+0000
1.00000000000000E+0000 0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
3.00000000000000E+0000 0.00000000000000E+0000
При x00 = -5; x11 = 5 и eps0 = 0.000049 получится тот же результат вследствие «эталонной» отделенности корней. В данном трансцендентном уравнении все корни совпали с корнями полинома (6), входящего в рассматриваемую суперпозицию (15).
Замечание 7. Предложенный метод поиска корней полиномов и аналитических функций, как правило, на практике находил все корни без пропуска и каждый из них без потери значащих цифр в формате extended представления числовых данных в Delphi. Это объяснялось тем, что в реализующей метод программе не производилось никакой вычислительной обработки входных значений полиномов и функций. Сортировка только сравнивала их значения, но не производила их преобразования. Во всех процедурах и операторах программы эти значения по-прежнему только сравнивались, но не преобразовывались (рис. 1–3). Однако предложенный метод не всегда может сохранять это качество при решении трансцендентных уравнений. Переход от (13) к (14) всегда требует вычитания входных значений. Такая операция использует выравнивание порядков чисел в формате с плавающей точкой, которая (в силу «механического» сдвига мантиссы на ограниченной разрядной сетке) может повлечь потерю значащих цифр мантиссы числа в результате. Это усугубляется при сложении быстро растущих и быстро убывающих функций-слагаемых. Как следствие, в случае сложных функций при выполнении операции (14) точность метода, характерная при поисках корней полиномов и аналитических функций, может не сохраняться в случае решения трансцендентных уравнений.
Нетрудно сконструировать примеры и указать случаи, когда при решении трансцендентных уравнений рассматриваемым компьютерным способом будут происходить потери корней, искажение их значений и даже отсутствие результатов решения. Тем не менее иногда эта проблема решается переходом к меньшему радиусу локализации.
Пример 11. Пусть рассматривается уравнение
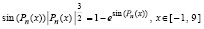, (16)
где n = 11 и
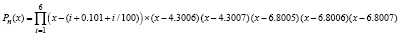. (17)
Задачу (16), (17) программа решает правильно только при уменьшенном радиусе локализации eps0 = 0.0000049. Для краткости решение приводится непосредственно на промежутке x00 = -1; x11 = 9; соответственно (14) применительно к (16), (17) подпрограмма func примет вид
function func (var x: extended): extended;
var i1: 1..n1;p:extended;
begin p: = 1; for i1: = 1 to 11 do p: = p*(x-b[i1]);
func: = abs(sin(P)*sqrt(abs(p*p*p))-1+exp(sin(p)));
end.
Программа корректируется для задания корней с помощью массива b. В результате работы программы получатся правильные корни, представляющие решение задачи (16), (17):
1.11100000000000E+0000 0.00000000000000E+0000
2.12100000000000E+0000 0.00000000000000E+0000
3.13100000000000E+0000 0.00000000000000E+0000
4.14100000000000E+0000 0.00000000000000E+0000
4.30060000000000E+0000 0.00000000000000E+0000
4.30070000000000E+0000 0.00000000000000E+0000
5.15100000000000E+0000 0.00000000000000E+0000
6.16100000000000E+0000 0.00000000000000E+0000
6.80050000000000E+0000 0.00000000000000E+0000
6.80060000000000E+0000 0.00000000000000E+0000
6.80070000000000E+0000 0.00000000000000E+0000
Некоторые из корней априори отличались на 0.0001.
Изложенный компьютерный метод оценки области действительных корней полиномов указывает не только границы области, но позволяет получить структуру расположения корней с помощью их идентификации. В этом состоит отличие от аналитических методов, представленных во введении, и от других известных методов оценки области корней, в частности [15]. В идентифицированных границах посредством уменьшения радиуса локализации метод позволяет найти все действительные корни. При этом не используются математические преобразования полиномов, но используются только их значения на каждом шаге дискретизации, а также сравнения значений, что в целом обуславливает относительно высокую точность идентификации корней. На входе метода полином может определяться значениями без использования коэффициентов, задание значений может быть неявным. Без существенных изменений метод переносится на идентификацию области и самих действительных корней аналитической функции, представимой в языке программирования, аналогично, применим к поиску действительных корней неаналитических функций и трансцендентных уравнений. Метод реализуется по единой программе стандартного вида. В качестве ограничения в применении необходимо учитывать опасность выхода из числового диапазона при вычислении входных значений функций. Как показывают приведенные выше примеры и результаты численного эксперимента, выход из границ диапазона не всегда удается указать априори. К недостаткам метода относится то, что корни функции идентифицируются без учета кратности. Вместе с тем в случае полинома кратность корня можно определить его подстановкой в производные последовательных порядков от этого полинома. Метод является прикладным, сугубо компьютерным, не имеет аналитической формы, поэтому непригоден для теоретических оценок. Элементы метода обсуждались в [12, 13], но неполно: не было обоснования идентификации границ области корней полиномов, исследование не относилось к случаям аналитических функций и корней трансцендентных уравнений.
Численные эксперименты, при отмеченных ограничениях, в большинстве случаев показывают достоверность работы, реализующей метод программы. При этом необходим правильный выбор радиуса локализации, который при отсутствии информации о расстоянии между корнями всегда следует брать с существенным запасом малости.
Заключение
Изложен компьютерный метод идентификации области, структуры расположения и значений действительных корней полинома на основе применения устойчивой адресной сортировки слиянием. Метод распространяется на идентификацию корней аналитических функций, функций общего вида и корней трансцендентных уравнений. При ограничениях, исключающих выход из числового диапазона, идентификация границ совмещается с идентификацией непосредственно самих корней функции, как правило, без их пропуска, с точностью до представления числовых данных в Delphi. Метод реализуется с помощью единой программы стандартного вида.