Введение
Аэроаквапонные установки представляют собой замкнутые экосистемы, в которых происходит взаимосвязанное выращивание растений и водных организмов [1, 2]. В таких системах растения получают питательные вещества из воды, обогащенной продуктами жизнедеятельности рыб, а растения, в свою очередь, очищают воду. Это позволяет создать практически безотходное производство с высокой эффективностью использования ресурсов [3, 4].
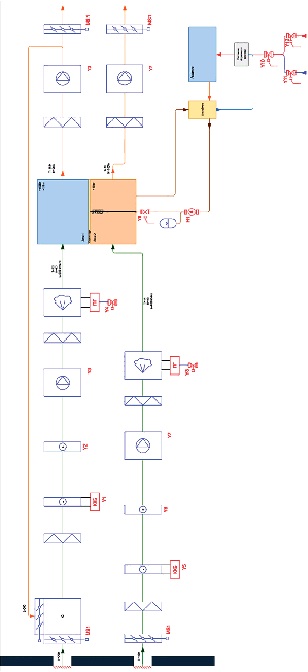
Схема вентиляции и водоснабжения аэроаквапонной установки Источник: составлено авторами
Особое значение аэроаквапоника приобретает в условиях городских территорий, где ограничен доступ к земельным участкам [5]. Кроме того, данная технология позволяет осуществлять круглогодичное выращивание сельскохозяйственных культур независимо от климатических условий, что делает ее особенно привлекательной для промышленного применения [6].
Практическая ценность исследования выражается в том, что его результаты могут быть использованы для разработки систем автоматического управления аэроаквапонными установками. Это, в свою очередь, приведет к увеличению их производительности и будет способствовать экономической целесообразности.
Цель исследования – определение управляющих воздействий для технологического процесса выращивания картофеля в аэроаквапонной установке.
Материалы и методы исследования
Все исследования проводились на базе Российского технологического университета МИРЭА.
На рисунке представлена схема вентиляции и водоснабжения аэроаквапонной установки. Вентиляционная подсистема выполнена по двухкамерной схеме [5] с последовательным расположением компонентов в приточном контуре: регулируемая воздушная заслонка, камера смешивания для верхней камеры установки, фильтрующий элемент грубой очистки воздуха, компрессорно-конденсаторный блок (обозначения Y1, Y5), трубчатый электронагреватель (Y2, Y6), вентилятор (Y3, Y7), фильтр тонкой очистки воздуха и парогенератор (Y4, Y8). В вытяжном контуре реализована аналогичная конфигурация оборудования: фильтр очистки воздуха, вентилятор и регулируемая воздушная заслонка. Водяная подсистема включает в себя рыбоводный аквариум, резервуар-отстойник для загрязненной воды, осмотическую установку водоочистки, регулирующие клапана и насосный агрегат высокого давления (H1) с гидроаккумулятором.
Методологическая база включает разработку дифференциальных уравнений для описания изменения температуры и влажности в верхней и нижней камерах, а также параметров водной среды в аквариуме. Особое внимание уделяется анализу нелинейности и нестационарности системы, что требует применения численных методов управления. В работе используются пропорционально-интегральные регуляторы для контроля кондиционеров, трубчатых электронагревателей, парогенераторов и клапанов подачи воды, а также рассматривается возможность применения дискретного управления для некоторых элементов системы. Исследование учитывает сезонность работы установки, что позволяет создать эффективную систему управления технологическими процессами выращивания картофеля [7, 8].
Для обеспечения точности и надежности управления проведен детальный анализ взаимосвязей между управляющими сигналами и их влиянием на различные параметры системы [9, 10]. Моделирование включает разработку систем уравнений, описывающих тепловой и материальный баланс, взаимосвязь концентрации аммиака и pH, а также температурный режим воды в аквариуме.
Результаты исследования и их обсуждение
Поскольку система является двухкамерной [1], следует рассматривать каждую камеру по отдельности.
Также стоит учитывать сезонность работы установки, так как в зимний сезон процесс изменения температуры значительно отличается от изменений ее в летний сезон [11, 12].
Классический подход получения математической модели технологического процесса базируется на уравнениях материального и теплового баланса. Исходные уравнения (1), (3), (8), (13) и (15) составлены авторами в соответствии с особенностями функционирования установки (рисунок).
Исходным уравнением для получения модели «подача воздуха – температура в верхней камере летом» является уравнение теплового баланса без учета тепловых потерь, которое будет иметь вид:
vк1 × Своз × (Ттэн1 – Тккб1 + Ткс) × dt = (mб × Сб) × dTкл1, (1)
где vк1 – массовый расход воздуха, продуваемого через верхнюю камеру, л/с; Своз – удельная теплоемкость воздуха, Дж/(оС * кг); Ттэн1 – температура воздуха после трубчатого электронагревателя (ТЭН), оС; Тккб1 – температура воздуха после теплообменника компрессорно-конденсаторного блока (ККБ), оС; Ткс – температура воздуха после камеры смешивания с вытяжным воздухом, оС; mб – масса ботвы, кг; Сб – удельная теплоемкость ботвы, Дж/(оС * кг); dTкл1 – приращение температуры воздуха в верхней камере летом за время dt, оС.
Запишем выражение для определения приращения температуры в верхней камере:
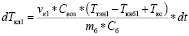. (2)
Расход среды в общем виде определяется выражением:
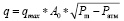, (3)
где q – массовый расход среды через регулирующий орган, кг/с; qmax – массовый расход среды через регулирующий орган при перепаде давления на нем 0,1 МПа, кг/(Па * с); A0 – степень открытия регулирующего органа; Pm – давление в магистрали, Па; Pатм – атмосферное давление, Па.
Подставляя в формулу (2) выражение (3), без учета инерционности исполнительного механизма, получаем искомое дифференциально выражение:
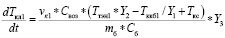, (4)
где Y1 – управляющий сигнал мощностью ККБ; Y2 – управляющий сигнал мощностью ТЭНа; Y3 – управляющий сигнал мощностью двигателей, обеспечивающих газообмен в верхней камере.
Поскольку в зимний период единственное отличие в работе – это отсутствие осушения и охлаждение [13, 14], то ККБ в расчетах не учитывается и выражение (4) будет иметь вид:
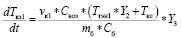, (5)
где dTкз1 – приращение температуры воздуха в верхней камере зимой за время dt, оС.
Так как нижняя камера отличается от верхней только отсутствием камеры смешивания и распылением дополнительной влаги (питательного раствора), то уравнения для летнего (4) и зимнего (5) режимов будут иметь вид:
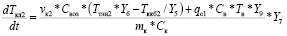, (6)
где qc1 – массовый расход воды через клапан аэрационной системы, л/с; Cв – удельная теплоемкость воды, Дж/(оС * кг); Тв – температура воды, поступающей в систему, оС; dTкл2 – приращение температуры воздуха в нижней камере летом за время dt, оС; Y5 – управляющий сигнал мощностью ККБ; Y6 – управляющий сигнал мощностью ТЭНа; Y7 – управляющий сигнал мощностью двигателей, обеспечивающих газообмен в нижней камере; Y9 – управляющий сигнал клапаном аэрации.
С учетом указанных выше особенностей работы в зимний период получаем, что выражение (8) будет иметь вид:
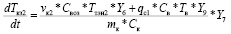, (7)
где dTкз2 – приращение температуры воздуха в нижней камере зимой за время dt, оС.
Исходным уравнением для получения модели по каналу «переосушение и увлажнение воздуха – влажность воздуха в верхней камере летом» является уравнение материального баланса, имеющее вид:
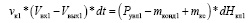, (8)
где vк1 – массовый расход воздуха, продуваемого через верхнюю камеру, л/с; Vвх1 – начальное влагосодержание воздуха на входе, г/кг; Vвых1 – конечное влагосодержание воздуха на выходе, г/кг; Рувл1 – производительность увлажнителя, л/с; тконд1 – масса конденсата на выходе ККБ, л/с; ткс – приращение влагосодержания после камеры смешивания, л; dHкл1 – приращение влажности в верхней камере установки за время dt, учитывающее естественное испарение влаги с поверхности листьев летом, кг.
Подставляя в формулу (10) выражение (3), без учета инерционности исполнительного механизма, получаем искомое дифференциально выражение:
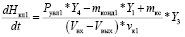, (9)
где Y1 – управляющий сигнал мощностью ККБ; Y3 – управляющий сигнал мощностью двигателей, обеспечивающих газообмен в верхней камере; Y4 – управляющий сигнал клапаном подачи воды для повышения влажности входящего в верхнюю камеру воздуха.
С учетом указанных выше особенностей работы в зимний период получаем, что выражение (9) будет иметь вид:
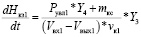, (10)
где dHкз1 – приращение влажности в верхней камере установки за время dt, учитывающее естественное испарение влаги с поверхности листьев зимой, кг.
Так как нижняя камера отличается от верхней только отсутствием камеры смешивания и распылением дополнительной влаги (питательного раствора), то уравнения для летнего (9) и зимнего (10) режимов будут иметь вид:
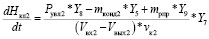, (11)
где mрпр – масса распыленного питательного раствора, л/с; dHкл2 – приращение влажности в нижней камере установки за время dt, учитывающее естественное испарение влаги с поверхности листьев летом, кг; Y5 – управляющий сигнал мощностью ККБ; Y7 – управляющий сигнал мощностью двигателей, обеспечивающих газообмен в нижней камере; Y8 – управляющий сигнал клапаном подачи воды для повышения влажности входящего в нижнюю камеру воздуха; Y9 – управляющий сигнал клапаном аэрации.
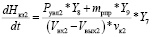, (12)
где dHкз1 – приращение влажности в верхней камере установки за время dt, учитывающее естественное испарение влаги с поверхности листьев зимой, кг.
Экспериментальные данные указывают на необходимость поддержания постоянного уровня pH в течение всего периода выращивания, поскольку его отклонения от оптимального значения существенно влияют на продуктивность. Постоянный контроль pH осуществляется в аквариуме с рыбами.
Рыбы в процессе жизнедеятельности [15] выделяют аммиак (NH3), который, взаимодействуя с водой, образует гидроксид аммония (NH4OH), что приводит к повышению pH в зависимости от концентрации. Концентрация аммиака и pH связаны уравнением Генри. При температуре 22–24°C и нормальном атмосферном давлении:
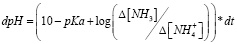, (13)
где dpH – изменение показателя pH раствора; Δ[NH3] – изменение концентрации аммиака;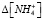 
– изменение концентрации ионов аммония; pKa – диссоационная константа основания конкретного соединения (для NH3 равна примерно 9,25).
Поскольку NH3 является слабым соединением, концентрация ионов аммония приблизительно равна концентрации аммиака. При концентрации NH3 в 1 моль/л pH составляет 9,25, что значительно выше оптимального уровня.
Для поддержания оптимального pH необходимо его постоянное снижение. Это достигается мониторингом pH и регулярным обновлением воды. Грязная вода направляется в отстойники для получения концентрата аммиака, а лишняя вода смешивается с внешней водой, проходит через системы обратного осмоса, минерализации и аэрации, после чего возвращается в аквариум с заданным pH.
В концентрат аммиака добавляются минеральные вещества для получения оптимального раствора по питательным веществам и pH.
Подставляя в формулу (13) выражение (3), без учета инерционности исполнительного механизма, получаем искомое дифференциально выражение:
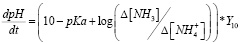, (14)
где Y10 – управляющий сигнал клапаном подачи воды в аквариум.
Исходным управлением для получения модели «Изменение температуры подаваемой воды – температура в аквариуме» является уравнение теплового баланса без учета тепловых потерь, которое будет иметь вид:
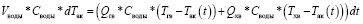(15),
где Vводы – общий объем воды, л; Своды – удельная теплоемкость воды, Дж/(оС * кг); Qгв – объем горячей воды, поступающей в аквариум, л/мин; Qхв – объем холодной воды, поступающей в аквариум, л/мин; Тгв – температура горячей воды, оС; Тхв – температура холодной воды, оС; Так(t) – температура воды в аквариуме в момент времени dt, оС; dТак – приращение температуры воды в аквариуме за время dt, оС.
Запишем выражение для определения приращения температуры в аквариуме:
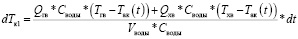. (16)
Подставляя в формулу (16) выражение (3), без учета инерционности исполнительного механизма, получаем искомое дифференциально выражение:
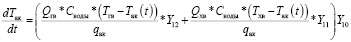, (17)
где Y10 – управляющий сигнал клапаном подачи воды в аквариум; Y11 – управляющий сигнал открытия клапана с холодной водой; Y12 – управляющий сигнал открытия клапана с горячей водой.
В качестве переменных состояния для предполагаемой системы управления процессом выращивания картофеля принимаем:
x1 – температура воздуха в верхней камере, Tк1;
x2 – температура воздуха в нижней камере, Tк2;
x3 – влажность воздуха в верхней камере, Нк1;
x4 – влажность воздуха в нижней камере, Нк2;
x5 – уровень pH в аквариуме, рН;
x6 – температура воды в аквариуме, Tак.
Проанализируем полученные уравнения (1–17) математических моделей с добавленными управляющими параметрами и преобразуем их в форму дифференциальных уравнений первого порядка относительно первой производной переменной состояния. Для упрощения последующей работы введем новые обозначения.
Так, для модели изменения температуры воздуха в верхней камере летом получаем:
Так, для модели изменения температуры воздуха в верхней камере летом получаем:
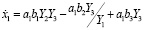, (18)
где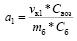 
; b1 = Tтэн1; b2 = Tккб1; b3 = Tкс.
Для модели изменения температуры воздуха в верхней камере зимой получаем:
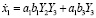. (19)
Для модели изменения температуры воздуха в нижней камере летом получаем:
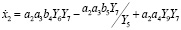, (20)
где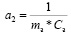 
; а3 = vк2 * Cвоз;
а4 = qc1 * Cв * Tв; b4 = Tтэн2; b5 = Tккб2.
Для модели изменения температуры воздуха в нижней камере зимой получаем:
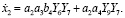(21)
Для модели изменения влажности воздуха в верхней камере летом получаем:
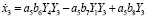, (22)
где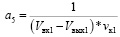 
;
b6 = Рувл1; b7 = mконд1; b8 = mкс.
Для модели изменения влажности воздуха в верхней камере зимой получаем:
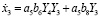. (23)
Для модели изменения влажности воздуха в нижней камере летом получаем:
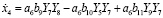, (24)
где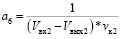 
;
b9 = Рувл2; b10 = mконд2; b11 = mрпр.
Для модели изменения влажности воздуха в нижней камере зимой получаем:
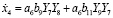. (25)
Для модели изменения параметра pH воды в аквариуме получаем:
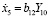, (26)
где
.
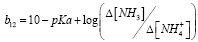Для модели изменения температуры воды в аквариуме получаем:
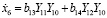, (27)
где
.
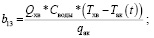
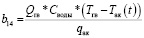Из полученных уравнений наглядно видно, что многие управляющие сигналы пересекаются друг с другом по воздействиям на систему. С учетом этого систему уравнений, которая описывает перемещение системы в пространстве переменных состояния, представим как:
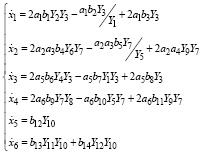
(28)
Система уравнений (28) моделирует движение объекта в пространстве состояний. Ввиду наличия произведений переменных состояний, которые изменяются в процессе функционирования системы, данная система характеризуется как нелинейная и нестационарная. В такой форме невозможно найти аналитическое решение задачи оптимального управления, поэтому целесообразно применять численные методы. При этом важно учитывать вопросы существования и оптимальности решения.
Проанализируем систему, поведение которой определяется формулой (28). В управляющей подсистеме определена область регулирования Y. Приемлемыми способами управления являются любые кусочно-непрерывные функции Y(t)=(Y1(t), …, Y12(t)), значения которых находятся в пределах области Y. В фазовом пространстве Х выделены начальная точка х0 и целевая точка х1.
Выбор типов управляющих воздействий
|
Дискретное управление |
Непрерывное управление |
|
Y3, Y7 (вентиляторы) |
Y1, Y5 (ККБ) |
|
Y9 (клапан подачи воды в нижнюю камеру) |
Y2, Y6 (ТЭН) |
|
Y10 (клапан подачи воды в аквариум) |
Y4, Y8 (парогенератор) |
|
Y11 (клапан подачи холодной воды) |
|
|
Y12 (клапан подачи горячей воды) |
Примечание: составлено авторами.
Траектория движения системы (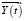
, x(t)) от начального момента до времени Т считается оптимальной, если она обеспечивает переход из начального состояния х0 в конечное х1 за минимальное время и с наилучшим качеством управления, выраженным в минимуме функционала. Для каждой фазы процесса выращивания картофеля в аэроаквапонной установке можно сформировать стратегию управления.
Проведенные экспериментальные исследования в области управления процессом аэроаквапоники в установке (рисунок) позволили сформировать практические рекомендации по выбору типов управляющих воздействий (таблица).
Полученные уравнения для летнего периода (4), (6), (9), (11), (14), (17) и зимнего периода (5), (7), (10), (12), (14), (17) с точностью 94,3 % (для лета) и 92,7 % (для зимы) описывают динамику исследуемых процессов. Сравнение производилось с экспериментальными данными, полученными авторами в период с июля по сентябрь 2024 г. и с декабря по февраль 2025 г.
Заключение
В ходе исследования были разработаны комплексные математические модели технологических процессов аэроаквапонной установки для выращивания картофеля. Модели описывают температурные режимы в камерах установки для разных сезонов эксплуатации, учитывают нелинейность и нестационарность системы, что требует применения численных методов управления. Созданы модели контроля влажности воздуха с учетом процессов испарения и увлажнения, а также модель управления pH в аквариуме, учитывающая влияние аммиака и необходимость обновления воды. Разработаны математические описания температурных режимов воды в аквариуме с учетом подачи горячей и холодной воды. Анализ показал взаимосвязь управляющих сигналов, что требует использования ПИ-регуляторов для точного поддержания параметров в заданных пределах.