Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 1,172

Введение

Система остаточных классов (СОК) является альтернативой двоичной системе счисления и представляет собой перспективный способ ускорения арифметических вычислений. Благодаря возможности параллельной обработки чисел с небольшой разрядностью СОК существенно уменьшает время выполнения операций сложения, вычитания и умножения [1]. Эти преимущества делают СОК особенно привлекательной для задач, в которых преобладают модульные арифметические вычисления [2]. Широкое применение данный подход находит в цифровой обработке сигналов [3; 4]. Так, на основе вычислений в СОК решается ряд задач по цифровой фильтрации видеосигналов [5] и интеллектуальному анализу визуальных данных [6; 7], разработке отказоустойчивых модулярных нейрокомпьютеров [8]. СОК применяют в том числе для различных задач в области криптографии [9; 10]. Облачные технологии [11] и беспроводные сенсорные сети [12] – это области, которые требуют наличия высокопроизводительных и надежных решений на основе СОК. В настоящее время активно разрабатываются подобные решения для спутниковой связи [13; 14], вычислений на основе ДНК [15] и во многих других направлениях.

Тем не менее СОК имеет и определённые недостатки. Ключевая трудность заключается в реализации немодульных операций, таких как определение знака числа [16], сравнение чисел [17], обнаружение переполнения, деление, извлечение корня и некоторые другие. Поскольку эти операции не относятся к модульным, поиск эффективных методов их выполнения остаётся актуальной задачей. В последние годы было опубликовано множество работ, направленных на совершенствование алгоритмов выполнения таких операций в СОК для конкретных наборов модулей, например вида 2n ± 1, 2n ± 1 и т. д. [18; 19]. Современное развитие теории СОК отличается множеством узкоспециализированных исследований, сосредоточенных на отдельных наборах модулей, которые зачастую не пересекаются между собой. Это приводит к тому, что модульный набор, эффективный для одной задачи, может оказаться совершенно неприменимым для другой, что подробно представлено в работе авторов Kaplun D. и др. [20]. Такое положение дел значительно усложняет практическое использование СОК из-за разнообразия и несогласованности существующих решений, а также отсутствия универсальных и эффективных подходов. Исследователями Younes и Steffan была предпринята попытка обобщить существующие подходы к выполнению операций сложения и умножения в различных реализациях СОК [21].

Одной из основных проблемных операций в СОК является определение знака числа. Эта операция играет фундаментальную роль, поскольку служит основой других сложных в СОК операций, таких как сравнение чисел и деление. В настоящее время разработаны эффективные алгоритмы определения знака, однако они применимы лишь к СОК с определёнными, специально подобранными наборами модулей. Авторами Xu, Bian, Yao предложен алгоритм определения знака для СОК вида {2n+1–1, 2n–1, 2n}, однако скорость проведения операции представляется недостаточной [22]. Tomczak разработал новый алгоритм определения знака в СОК вида {2n–1, 2n, 2n+1}, требующий больших аппаратных затрат [23]. Mohan и Phalguna также оценивают данный набор модулей для двух методов получения чисел со смешанным основанием счисления, что доказывает необходимость высоких аппаратных затрат [24]. Setiaarif и Siy предложили алгоритм определения знака, требующий построения модулей СОК по заданным условиям [25]. Kumar и Chang разработали новый подход к решению задачи сравнения чисел в СОК для специализированного набора из пяти оснований 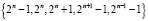, что позволяет повысить энергоэффективность, однако скорость вычислений недостаточна [26]. Особенность подхода заключается в том, что знаки операндов при сравнении, а также их разность определяются после масштабирования на коэффициент (22n–1)(2n–1–1), что позволяет уменьшить размер сумматоров по модулю с 5n бит до n и n+1 бит. Однако все известные работы по данной проблеме имеют общий недостаток, заключающийся в ограниченности применения на практике. Для устранения этой проблемы необходимо разработать новые методы и алгоритмы определения знака числа в СОК, пригодные для произвольных конфигураций модулей, что обосновывает выбор цели исследования.

Целью исследования является разработка нового алгоритма определения знака числа в СОК на основе Китайской теоремы об остатках с вычислениями над дробными величинами.

Материалы и методы исследования

В данном исследовании применен новый подход к определению знака числа в СОК на основе преобразования метода вычислений по Китайской теореме об остатках над кольцом целых чисел к вычислениям над дробными числами. Такой подход привел к увеличению разрядности обрабатываемых чисел, однако позволил избежать вычислительно сложной операции деления чисел. С использованием классических математических методов была доказана теорема, подтверждающая корректность выполнения операции определения знака числа в СОК на основе предложенного алгоритма. Для оценки эффективности алгоритма была проведена его программная реализация на языке Python с моделированием в различных СОК, имеющих динамические диапазоны от 256 до 2048 бит включительно. Кроме того, было выполнено сравнение предложенной разработки с известным алгоритмом на основе обобщенной позиционной системы счисления.

Результаты исследования и их обсуждение

СОК задаётся множеством положительных взаимно простых между собой чисел {m1, m2, …, mn}, называемых модулями. Произведение этих модулей M = m1m2…mn определяет диапазон СОК. В рамках такой системы любое целое число X, которое находится в интервале 0 ≤ X < M, можно однозначно представить в виде набора остатков (x1, x2, …, xn), где xi вычислен как остаток от деления X на соответствующий модуль mi.

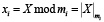, 0 ≤ xi < mi. (1)

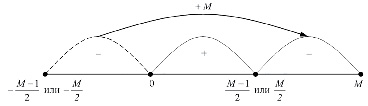
Рис. 1. Визуализация расположения положительных и отрицательных чисел в СОК

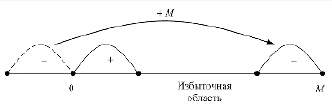
Рис. 2. Визуализация расположения положительных и отрицательных чисел в избыточной СОК

Положительные и отрицательные числа в СОК представляются за счет условного деления диапазона M на две примерно равные части, при этом одна часть соответствует положительным числам, другая – отрицательным. Знак числа X определяется тем, в какую из данных частей оно попадает:

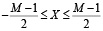, если M нечетное, (2)

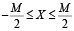, если M четное.

Это условие определяет однозначность представления числа X в СОК. На рисунке 1 представлено распределение положительных и отрицательных чисел в системе остаточных классов на числовой оси. Отрицательные значения, входящие в соответствующие диапазоны (2), смещены вправо на M единиц, что обеспечивается циклической природой представления чисел в СОК на основе алгебры колец классов вычетов.

Арифметические операции сложения, вычитания и умножения в СОК реализуются по следующим правилам:

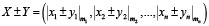(3)

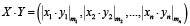(4)

В формулах (3) и (4) проявляется главное достоинство СОК – указанные операции выполняются параллельно по каждому из модулей.

При разработке отказоустойчивых систем применяется избыточная система остаточных классов (RRNS). В такой системе модули делятся на информационные и дополнительные (избыточные). Благодаря включению избыточных модулей полный диапазон системы становится больше, чем диапазон её информационной части. Разряды СОК по избыточным модулям на практике используются для обнаружения и исправления ошибок вычислительной системы. На рисунке 2 продемонстрировано расположение положительных и отрицательных чисел в избыточной СОК.

Целью данной статьи является разработка эффективных алгоритмов для определения знака числа, заданного в виде набора остатков (x1, x2, …, xn). В дальнейшем будет представлен новый метод, позволяющий проверять, принадлежит ли число интервалу положительных или отрицательных значений в СОК, как это показано на рисунках 1 и 2. Математической основой вычисления позиционной характеристики числа в СОК является его преобразование в позиционную форму представления. Преобразование осуществляется на базе Китайской теоремы об остатках (КТО, CRT), что обеспечивает однозначное восстановление значения по его представлению в вычетах. Пусть в СОК с модулями m1, m2, …, mn задано число X, удовлетворяющее неравенству 0 ≤ X < M = m1m2…mn и представленное в виде набора остатков X = (x1, x2, …, xn). Восстановление исходного числа X по этим остаткам выполняется согласно выражению (6):

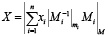, (5)

где Mi = M / mi , а 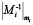это мультипликативная обратная величина для числа 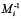по модулю mi.

Разделив обе части равенства (5) на M, получим:

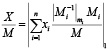, (6)

в котором | |1 означает дробную часть числа.

Положив 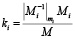, тогда преобразуем выражение (6) в компактную форму:

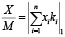. (7)

Все значения 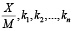в формуле (7), которые представляют собой бесконечные периодические дроби, лежат в интервале [0,1). Коэффициенты ki зависят только от выбранных модулей СОК и, следовательно, являются её априорными характеристиками.

Сопоставление формул (5) и (7) позволяет выделить ряд отличий, имеющих практическое значение. Формула (5) требует выполнения операции нахождения остатка по большому модулю M, что на практике связано с высокой вычислительной сложностью. В формуле (7) указанная операция заменяется определением дробной части числа, что значительно упрощает реализацию – фактически сводится к удалению целой части, то есть переноса в разряд единиц. Однако это преимущество сопровождается существенным недостатком: вычисления по формуле (7) требуют работы с бесконечными дробями. Тогда необходимо ответить на вопрос: с какой точностью необходимо производить вычисления по формуле (7), чтобы обеспечить корректное восстановление позиционного значения числа X на практике? Чтобы ответить на поставленный вопрос, введем методику определения знака числа в СОК, которая будет основана на применении Китайской теоремы об остатках и операциях с дробными значениями.

Обозначим через 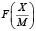бесконечную периодическую двоичную дробь, соответствующую отношению 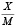. При усечении этой дроби, начиная с (N + 1)-го бита после запятой, получится конечная двоичная дробь, которую обозначим как .

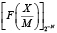Например, если ,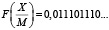

то .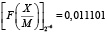

Для введенных величин выполняется неравенство

,

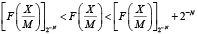описывающее положение на числовой оси точного значения 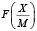относительно округленной величины .

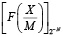В работе [27] была продемонстрирована высокая эффективность применения вычислений над дробными величинами для реализации проблемной операции деления в СОК. Далее покажем, как аналогичный подход может быть использован для реализации вычислительно сложной операции определения знака числа в СОК.

Пусть в вычислениях по формуле (7) используются округлённые значения вида 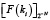. Следующая теорема предоставляет теоретическое обоснование корректности применения таких приближённых величин для точного восстановления чисел при обратном преобразовании из системы с дополнительным кодом (СОК) в позиционную систему счисления

Теорема 1. Минимальное значение N, обеспечивающее корректное преобразование числа X из СОК в позиционную систему счисления, согласно формуле

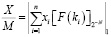, (8)

будет точным, равно

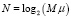, (9)

где .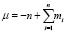

Доказательство. Очевидно, что

,

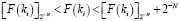для всех i = 1,2,…,n. Просуммировав последнее неравенство по всем модулям СОК, получим:

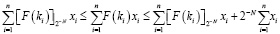. (10)

Величина 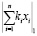отражает точное положение числа X на числовой оси. Для обеспечения точного определения значения X необходимо выбрать параметр N таким образом, чтобы в произвольный интервал 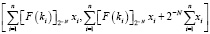попадало не более одного допустимого значения из диапазона системы СОК. Это требование эквивалентно условию .

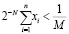Введем обозначение 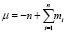. Наименьшее значение N, при котором возможно точное преобразование числа X из СОК в позиционную систему счисления с использованием формулы (8), определяется выражением 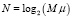, что и требовалось доказать.

Применение константы N, вычисленной по формуле (9), в формуле (8) для обратного преобразования числа X по вычислительной сложности приблизительно соответствует выполнению преобразования по формуле (5).

Точное местоположение X на числовой оси не является обязательным условием при определении его знака в СОК. Для корректного определения знака достаточно лишь узнать, в какой из интервалов, изображенных на рисунках 1, 2, попадает исследуемое число. Если использовать в формуле (8) вместо N уменьшенную величину Ñ, Ñ < N, то интервал (10) увеличится. При этом в интервал (10) могут попадать несколько дробей, соответствующих различным числам в СОК, поэтому использование Ñ для обратного преобразования не даст корректного результата. Однако при решении задачи об определении знака числа в СОК этот увеличенный интервал все еще может быть использован.

В произвольный промежуток 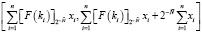могут попасть не более 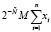дробей 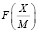, соответствующих различным числам в СОК.

Если учесть, что 0 ≤ xi < mi (формула (1)), то .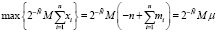

Для определения знака числа в СОК по его дробной части 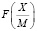необходимо учитывать следующие условия:

- если значение 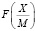удовлетворяет 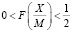, то число X является положительным;

- если 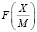удовлетворяет 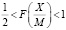, то число X отрицательное.

Ранее доказанная теорема 1 может служить теоретической основой для разработки нового алгоритма определения знака числа в СОК. Ниже представлен разработанный алгоритм определения знака числа в СОК, основанный на использовании величины 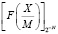, где N определяется по формуле (9).

Алгоритм

1. В СОК с модулями {m1, m2, …, mn} предварительно вычисляются константы

M = m1m2…mn, 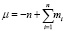, 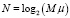и .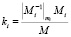

2. Для констант ki, определенных в пункте 1, определяются дробные величины .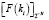

3. Вычисляется .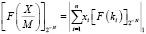

4. При условии 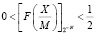, число X положительное.

Если 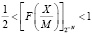, то X отрицательное.

Заданной точности N, из пунктов 5-6 приведенного алгоритма, достаточно для корректного определения знака числа в СОК. Это обеспечивается теоремой 1. Следующий пример демонстрирует работоспособность метода и его вычислительную сложность, сравнимую с применением классической КТО.

Пример 1. Пусть СОК задана основаниями m1 = 2, m2 = 3, m3 = 5 и m4 = 7.

Тогда , , ,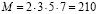

, , , .

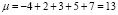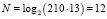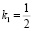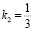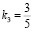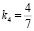Дроби, соответствующие константам ki, i = 1,…,4, будут иметь вид:

, ,

, .

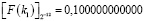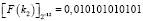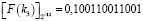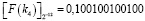Определим знак числа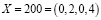

.

.

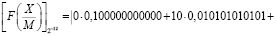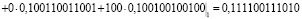Так как 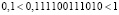, то число 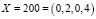отрицательное.

Далее будет показано, как применение разработанного алгоритма позволяет ускорить определение знака числа в СОК при программной реализации вычислительной системы.

С целью сравнения работы алгоритмов определения знака числа на основе метода быстрого преобразования в обобщенной позиционной системе счисления (ОПСС), описанного в [28], и на основе КТО с дробными величинами было проведено программное моделирование. Моделирование проводилось на языке Python 3.11. Для вычислений использовалась ЭВМ с процессором Intel Core i5-12450H, с 16 ГБ оперативной памяти и 64-битной операционной системой Windows 10. Для моделирования предложенного алгоритма были выбраны СОК, представленные в таблице 1. Данный выбор объясняется тем, что представленные наборы модулей COK1 – COK6 позволяют представить востребованные на практике числовые диапазоны от 256 до 2048 бит.

Таблица 1

Наборы модулей СОК, перекрывающие различные динамические диапазоны

Примечание: составлено автором на основе проведенных вычислений.

Таблица 2

Время работы алгоритмов определения знака числа в СОК

Примечание: составлено автором с использованием разработанного алгоритма и метода из источника [28].

Критерием для сравнения алгоритмов выбрано время выполнения, выраженное в секундах. Было проведено 1 000 000 итераций для каждого из алгоритмов во всех моделируемых случаях. В таблице 2 приведены результаты моделирования алгоритмов с указанием среднего времени выполнения.

Предложенный алгоритм выигрывает в скорости во всех рассмотренных случаях. Для COK1 время работы сокращается в ≈1.5 раза по сравнению с алгоритмами на основе MRC. В случае COK2 время работы сокращается в ≈1.8 раза. Для COK3 сокращение временных затрат составляет ≈1.4 раза. Для COK4 время сокращается в ≈3.5 раза. Для COK5 время сокращается в ≈2.2 раза. Наконец, для COK6 время работы сокращается в ≈2.9 раза. Другими словами, время работы предложенного алгоритма составляет 34–67% от времени работы алгоритма из [28]. Указанные цифры зависят от выбранной СОК и ее характеристик: модулей, их количества и т.д.

Данные из таблицы 2 позволяют сделать вывод о том, что предложенный алгоритм быстрее известного аналогичного алгоритма определения знака числа в СОК с модулями произвольного вида. Продемонстрированный результат может быть использован для разработки новых способов реализации проблемных операций СОК – сравнения чисел и деления. Кроме того, более быстрое определение знака числа в СОК на основе предложенного метода позволит значительно расширить область практического применения СОК, особенно в области реализации систем машинного обучения и для цифровой обработки сигналов и изображений.

Заключение

Предложенный в статье алгоритм определения знака числа в СОК основан на модифицированной версии Китайской теоремы об остатках с использованием вычислений над дробными величинами. Результаты моделирования продемонстрировали, что данный алгоритм превосходит по скорости алгоритм на основе ОПСС. Предложенный в данной работе алгоритм является универсальным и не привязан к какому-либо набору модулей СОК. Данное обстоятельство может быть использовано в приложениях, использующих динамическое изменение параметров вычислительной системы.

Предложенный алгоритм определения знака позволяет ускорить данную проблемную операцию в СОК. Стоит отметить, что определение знака является базовой операцией для других проблемных задач, к которым относятся: сравнение чисел в СОК, деление в СОК, обнаружение переполнения диапазона, локализация ошибки и другие. Применение предложенного алгоритма позволит улучшить время выполнения перечисленных операций. Любое улучшение проблемных операций в СОК может расширить границы ее применения и найти новые приложения на практике, в которых СОК может быть использована с максимальной эффективностью, например в цифровой обработке сигналов, изображений и видео, а также в машинном обучении.