Введение
В металлургической, химической, горнообогатительной промышленности широко используются теплотехнические устройства прямого и косвенного нагрева разнообразных материалов, применяющиеся для различных тепловых воздействий, например сушки материала, обжига сырья, в том числе рудного. Важным аспектом современного подхода к проектированию теплотехнологического оборудования является возможность применения математического и компьютерного моделирования протекающих энергоемких процессов для обеспечения высоких показателей его энергетической эффективности. Детальное рассмотрение протекания процесса высокотемпературной подготовки материалов на примере обжига рудного сырья позволяет выявить пути совершенствования алгоритмов управления энергоемким теплотехнологическим оборудованием для отыскания оптимальных режимов работы. Под режимом нагрева понимается соблюдение определенных условий нагрева рудного материала во времени [1].
Цель исследования – разработка математических моделей и вычислительных процедур оптимального управления нагревом «термически тонких» и «термически массивных» тел в печи, обеспечивающих минимум по критерию расхода топлива и учитывающих особенности численного метода динамического программирования, проведение компьютеризированного расчета управляющего параметра – температуры газа, нагревающего плотный слой засыпки рудного сырья в многозонной проходной печи.
Материалы и методы исследования
Для всестороннего изучения протекания процесса высокотемпературной подготовки материалов на примере обжига рудного сырья в теплотехнологическом оборудовании горнообогатительной отрасли промышленности и отыскания оптимальных режимов работы, необходимо учесть технологические условия нагрева сырья с учетом различного рода технологических ограничений, зависящие от конструкции и назначения печи, от формы, размеров и расположения рудного материала в печи. Различают температурный и тепловой режимы нагрева материала [2]. Под температурным режимом понимают соблюдение определенного температурного закона нагрева рудного материала во времени. Под тепловым режимом понимают соблюдение определенного закона изменения тепловой нагрузки во времени. Тепловой и температурный режимы нагрева между собой взаимосвязаны. Чтобы обеспечить выполнение заданного температурного режима в печи, необходимо изменять количество тепла, подаваемого в печь в режиме реального времени.
В существующей практике нагревательных печей встречаются одно-, двух- и многоступенчатые режимы нагрева. Одноступенчатые режимы применяют для нагрева тонкого материала, так как при его нагреве исключено возникновение температурных напряжений и перепада температур по сечению тела [3, 4].
Применение камерного режима нагрева приводит к повышению производительности печи за счет форсирования нагрева и к ухудшению использования топлива в печи. Установлено, что снижение начального теплового потока до 50 % от максимального приводит к потере производительности до 15 %, но зато к резкому выигрышу в установочной мощности энергетического оборудования (тяги, давления газа, вентиляторов). Дальнейшее снижение теплового потока приводит к заметному увеличению длительности процесса нагрева рудного материала. На основании вышеизложенного возможно предположить значение оптимального начального теплового потока: qопт = 0.5. Реализация режима нагрева при постоянном тепловом потоке требует, чтобы тепловая мощность во времени нарастала по определенному закону, что затрудняет практическое осуществление такого режима. Реальным является режим при постоянной общей тепловой мощности печи [5]. Предложена методика расчета нагрева рудного материала при постоянной мощности. Установлено, что при постоянной мощности тепловой поток в начале первого периода нагрева на 10% больше, чем в конце того же самого периода.
Одной из задач металлургической и горно-обогатительной теплотехники является повышение эффективности использования ресурсов при строительстве и эксплуатации действующих агрегатов. Решению этой задачи способствует разработка и внедрение в практику научно обоснованных методов расчета оптимальных и конструктивных параметров печей различного типа и назначения [6]. Простейшие процессы нагрева тонких тел характеризуются системами с сосредоточенными параметрами и описываются обыкновенными дифференциальными уравнениями, устанавливающими зависимости характеристик процесса (температуры материала, газов и т.п.) от времени.
Более сложные процессы нагрева массивных тел характеризуются системами с распределенными параметрами и описываются дифференциальными уравнениями в частных производных, устанавливающими зависимость пространственного распределения характеристик от времени.
Траекторию нагрева «термически тонкого» тела обычно рассматривают в координатах температура – время. Более глубокие обобщения можно получить, если рассматривать процесс нагрева в фазовом пространстве. Состояние системы в любой момент времени τ можно характеризовать температурой t = t(τ) и ее скоростью tʹ = tʹ(τ). При этом между множеством состояний системы и точками на плоскости (t;tʹ) имеется взаимооднозначное соответствие. При движении точки на фазовой плоскости получаем фазовую траекторию. Задачей оптимального управления является: найти такие управляющие функции t(τ) и tʹ(τ), чтобы изображающая точка перешла из заданного начального состояния в начало координат и чтобы определенный критерий оптимальности, в данном случае расход топлива, достиг минимального значения.
Общая формулировка движения системы в фазовом пространстве дается принципом Гамильтона. Каждая система характеризуется функцией f0(t;tʹ). Пусть в моменты времени τ = τ1 и τ = τ2 система занимает положения
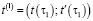и 
,
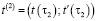тогда между этими положениями система движется таким образом, что интеграл действия (критерий оптимальности)
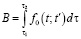
имеет наименьшее возможное значение. Для того чтобы интеграл B имел наименьшее значение, функция f0 должна удовлетворять дифференциальному уравнению Эйлера – Лагранжа:
.
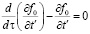При движении системы ряд ее величин (t;tʹ) изменяется со временем. Существуют, однако, такие функции этих величин, которые при движении сохраняют постоянное значение. Эти функции называют инвариантами движения, а их постоянство связано с однородностью пространства и времени. Используя закон сохранения, связанный с однородностью времени, и уравнение Эйлера – Лагранжа, приходим к функции Гамильтона Н, системы, пропорциональной энергии системы, которая остается неизменной при движении:
.
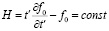Обозначив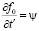 
, получим 
.
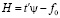Из последнего уравнения после дифференцирования получим соотношения, определяющие выбор траектории движения, обеспечивающий минимум интегралу действия
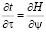и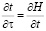 
.
Результаты исследования и их обсуждение
Рассмотрим задачу нагрева термически «тонкого тела», позволяющую при заданных условиях конвективного теплообмена в печи, времени нагрева и вида топлива выбрать такой температурный режим, при котором заданная конечная температура достигается при минимальном расходе топлива [7]. Такая постановка задачи позволяет обоснованно распространять решения на камерные печи, а в ряде случаев, при рассредоточенном подводе топлива и отводе дыма, на проходные печи [8].
Пусть изменение температуры t описывается уравнением
,
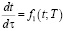где T – температура газов (управляющее воздействие), при условии: t(0) = t0 и t(τк) = tк .
Удельный расход топлива выражается интегралом:
,
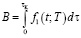где функция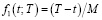 
, а мощность М = (Gc) / (αF), G – расход топлива, с – его теплоемкость, α – коэффициент теплоотдачи, F – поверхность. Таким образом, расход топлива составит:
,
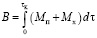где Mп – полезная мощность, равная
,
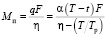Тр – расчетная (теоретическая) температура горения топлива, η – коэффициент использования топлива, Mх – мощность холостого хода.
В результате
, 
,
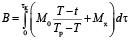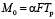тогда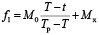 
,
а функция Гамильтона принимает вид
,
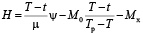где μ – постоянная, зависящая от интенсивности нагрева.
Для выбора режима нагрева, при котором расход топлива будет минимальным, принимается, что M0, Mх и μ не изменяются в процессе нагрева, а также, что оптимальная температура меньше допустимой. Эта температура в течение всего процесса нагрева должна быть такой, чтобы величина В имела максимальное значение для всех значений τ: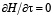 
.
Решение такой задачи получается в следующем виде:
температура материала –
;
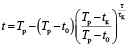температура газов –
.
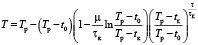Оптимальное значение полезной тепловой мощности
.
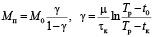Общий расход тепла
,
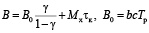где b – удельный расход тепла.
С увеличением времени нагрева первое слагаемое уменьшается, а второе – увеличивается. Это означает, что имеется такая оптимальная длительность нагрева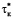 
, при которой расход топлива будет наименьшим.
Оптимальное время нагрева можно определить из условий H = 0 или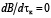 
, в виде
,
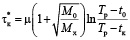оптимальная тепловая мощность при этом равна
.
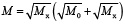При возрастании M оптимальное время нагрева уменьшается. Поэтому скоростной нагрев «термически тонких» тел выгоден при большой удельной мощности холостого хода печей, например секционных. При отсутствии ограничений оптимальная температура газов достигается при постоянной тепловой мощности, а затем нагрев ведется при предельно допустимой температуре газов [9].
Для оптимизации процесса нагрева при нелинейных граничных условиях, например передаче тепла излучением по закону Стефана – Больцмана, может быть эффективно применен метод динамического программирования. Этот метод не имеет общего алгоритма и заключается в последовательной оптимизации процесса нагрева на одном, двух и последующих этапах.
Нагрев «термически тонкого» тела в многозонной печи определяется температурой газов в каждой зоне или конечной температурой материала, при условии, что начальная температура материала задана [10]. Поэтапная оптимизация нагрева в многозонной печи заключается в следующем. Удельный расход тепла в k-й зоне n-зонной печи bk определяется соотношением
,
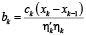где xk–1, xk – средняя температура материала в начале и конце k-й зоны печи, ηk – коэффициент использования тепла, ηk – отношение полезной мощности к общей мощности печи в k-й зоне. После преобразований получается bk = pLk, где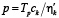 
, 
.
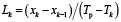Значение p одинаково для всех зон, поэтому расход топлива на участке, включающем n – m последних зон, определяется функцией
.
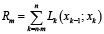Для всей печи
при m = 0 –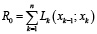 
.
Минимальное значение Rm, при заданном значении xk, характеризующее минимальный расход топлива на выделенном участке, обозначим через Фm. Связь между Rm и Фm имеет вид Фm = minRm. Минимальное значение R0, характеризующее расход топлива во всей печи, обозначим через Ф0 = minR0. Минимум отыскивается по переменным xk путем упорядоченной системы проверки различных вариантов значений xk при заданных t0 и tк. Неупорядоченная проверка вариантов потребовала во много раз большего количества вычислительных операций и практически неосуществима даже на мощных компьютерах [11]. Схема формирования аддитивно-сепарабельного критерия эффективности Ф представлена на рис. 1.
С физической точки зрения такой метод решения задачи заключается в отыскании такого распространения приращения теплосодержаний материала по зонам, при котором удельный расход топлива на печь был минимальным.
С математической точки зрения расчетная схема является численным решением рекуррентных нелинейных функциональных уравнений.
.
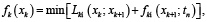
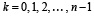Для расчета нагрева «термически тонкого» тела при граничных условиях третьего рода принимают выражения
,
,
,
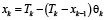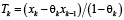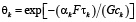где αk – средний для k-й зоны коэффициент теплоотдачи с учетом излучения и конвекции.
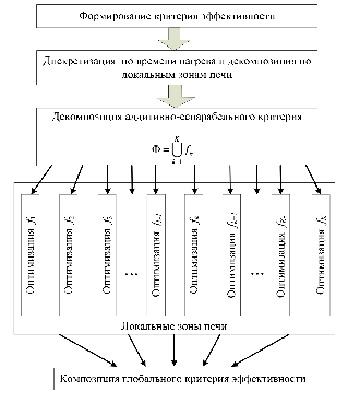
Рис. 1. Схема формирования аддитивно-сепарабельного критерия эффективности
Последовательность расчета четырехзонной печи следующая. Находят допустимый интервал изменения температур рудного материала в 1, 2 и 3-й зонах. Определяют расход топлива в третьей и четвертой зонах печи в виде функции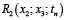 
и находят зависимость температуры x3(x2) и f2(x2). Определяют расход топлива во 2, 3 и 4-й зонах печи 
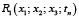и находят зависимость x2(x1) и f1(x1). Определяют общий расход тепла 
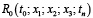, по которому находят f0 и оптимальную температуру в конце первой зоны. Осуществляя поэтапное движение от начала процесса к концу, находят оптимальные значения температур на границах 2-й и 3-й зон [12, 13].
Используя функции стабилизированного распределения температур по сечению массивного тела для стадии регулярного периода, можно полученные решения для тонких тел распространить на массивные тела.
dt / dτ = (T – t) / μʹ,
где t – среднеобъемная температура материала.
Выражения для температуры рудного материала, газов, тепловой мощности и расхода топлива оказываются аналогичными «термически тонким» телам и характеризуются заменой параметров α, μ, M0 на αʹ, μʹ, Mʹ0, учитывающих термическую массивность тела.
Оптимальное по расходу топлива время нагрева
,
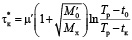оптимальная тепловая мощность при этом равна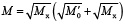 
. При выборе оптимального по расходу топлива режима нагрева массивных тел следует учитывать ограничения во втором периоде нагрева.
Разработана вычислительная методика для расчета нагрева массивного слитка в колодцах, состоящая из двух периодов: нагрева при оптимальной постоянной тепловой мощности до момента достижения заданной конечной среднеобъемной температуры с выдержкой при постоянном теплосодержании и определен удельный расход топлива.
Для решения задачи методом динамического программирования разделим время нагрева на четыре интервала. В течение первых двух интервалов нагрев ведется при постоянном тепловом потоке [14]. Этот режим в начале нагрева весьма близок к режиму нагрева при постоянной тепловой мощности и прост для расчета. В течение двух последних интервалов слиток нагревается при постоянной температуре газов. В течение третьего интервала температура газов принимает предельное максимальное значение равное 1350ºС. Продолжительность четвертого (последнего) интервала и температура газов выбираются из условия нагрева слитков до заданной конечной среднеобъемной температуры и достижения заданного конечного перепада температур по сечению [15]. Выбрав длительность последнего интервала и температуру газов, обеспечивающих конечный перепад по сечению, получаем заданную равномерность нагрева за определенное время [16]. Задачей вариационного расчета является выбор средних температур в конце 1-го x1, 2-го x2 и 3-го x3 интервалов, обеспечивающих в заданных ограничениях нагрев с минимальным расходом топлива. Вычислительная методика выбора оптимальных средних температур заключается в следующем.
На первом этапе расчета оптимизируются условия нагрева в 3-м и 4-м интервалах. Для этого для фиксированной средней температуры в конце 2-го интервала x2 варьируется средняя температура в конце 3-го интервала x3 и рассчитывается расход топлива в 3-м и 4-м интервалах R2 = L3 + f3. Определяется минимальное значение расхода топлива f2 = min{L3 + f3} и отвечающее ему значение средней температуры в конце 3-го интервала x3.
На втором этапе расчета оптимизируются условия нагрева на 2, 3 и 4-м интервалах. Для этого при фиксированной средней температуре в конце 1-го интервала x1 варьируется средняя температура в конце 2-го интервала x2 и рассчитывается расход топлива во 2, 3 и 4-м интервалах R1 = L2 + f2. Определяется минимальное значение расхода топлива f1 = min{L2 + f2} и отвечающее ему значение средней температуры в конце 2-го интервала x2.
На третьем этапе расчета оптимизируются условия нагрева в 1, 2, 3 и 4-м интервалах. Для этого при известной средней температуре металла в начале 1-го интервала (в начале нагрева t0) варьируется средняя температура в конце 1-го интервала x1 и рассчитывается расход топлива в 1, 2, 3 и 4-м интервалах R0 = L1 + f1. Определяется минимальное значение расхода топлива f0 = min{L1 + f1} в течение всего процесса нагрева и отвечающее ему значение средней температуры в конце 1-го интервала x1.
На 4-м этапе расчета осуществляется понятное движение, находим искомое значение температур x2 и x3.
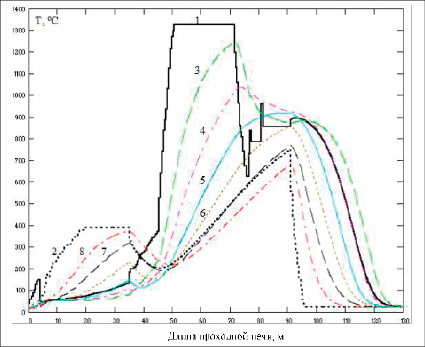
Рис. 2. Температура газа-теплоносителя над слоем рудного сырья (1) и под колосниковой решеткой (2). Температура в различных горизонтах плотного слоя рудного сырья сверху вниз (3–8). Оптимальный режим функционирования проходной печи
Характерной особенностью приведенного оптимального режима по сравнению с двухступенчатым является некоторое увеличение тепловых потоков в 3-м интервале нагрева за счет повышения температуры газов до предельно допустимого значения.
Применение разработанных вычислительных процедур поиска оптимальных условий нагрева рудного сырья в печах и колодцах с использованием предлагаемой методики позволяет выявить новые закономерности между характеристиками нагрева, которые могут быть полезными при конструировании теплотехнического оборудования, нормирования расхода топлива и совершенствования систем управления нагревом. Относительный расход топлива следует определять по формуле
VT = Bmin / BD , 0 < VT < 1,
где VT – оценка расхода топлива на данной печи в сравнении с оптимальным, Bmin – минимально возможный расход топлива, BD – действительный расход топлива. Также можно ввести оценку времени нагрева:
,
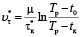при котором BD = Bmin. Рассматривая соотношение оптимального времени нагрева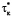 
к свободному времени нагрева τк в виде 
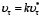, возможно установить, что величина VT определяется выражением:
,
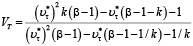где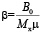 
.
Знание зависимости VT от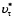 
, k и β позволит оценить потенциальный резерв экономии топлива в направлении изменения режима работы печи в сторону оптимизации.
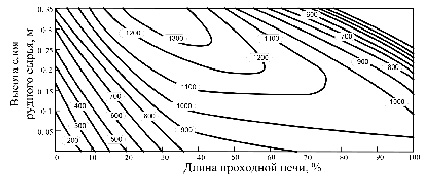
Рис. 3. Параметрическое семейство изолиний, показывающих температуру в плотном слое рудного сырья, в оптимальном режиме, ºС
По разработанным авторами вычислительным процедурам, реализованным в виде компьютерной программы на языке Borland C++, были определены оптимальные режимы функционирования многозонной печи, для нагрева рудного сырья в плотном слое высотой 0,35 м и шириной 1 м. Результаты расчета температуры газа-теплоносителя в оптимальном режиме функционирования печи представлены на рис. 2.
Найденный оптимальный режим функционирования проходной печи формирует тепловую волну, которая движется вглубь рудного материала в плотном слое засыпки и интенсифицирует процесс нагрева, рис. 3.
Заключение
Представлены математические модели и оригинальные вычислительные процедуры оптимального управления нагревом «термически тонких» и «термически массивных» тел, в печи для нагрева и высокотемпературной обработки рудного сырья, обеспечивающих минимум по критерию расхода топлива и учитывающие особенности численного метода динамического программирования. Представленные методики являются актуальным инструментом для построения цифровизированных двойников процессов, протекающих в реально функционирующем оборудовании, в частности с использованием предложенных вычислительных процедур был определен оптимальный режим функционирования многозонной печи, для нагрева рудного сырья в плотном слое шириной 1 м и высотой 0,35 м, используемой на предприятиях горнообогатительного комплекса промышленности для высокотемпературной обработки рудного сырья. Разработанные вычислительные процедуры оптимального управления нагревом рудного материала в печи и методика расчета нагрева рудного материала при постоянной мощности, обеспечивающие минимум по критерию расхода топлива и учитывающие особенности численного метода динамического программирования, позволяют увеличить эффективность использования ресурсов при минимальном значении расхода топлива, определить время нагрева при оптимальной постоянной тепловой мощности до момента достижения заданной конечной среднеобъемной температуры с выдержкой при постоянном теплосодержании, а также определить удельный расход топлива для дальнейшего поиска оптимальных режимов работы теплотехнологического оборудования в различных отраслях промышленности.