Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 1,172

Введение

Прогнозирование экономических показателей зародилось в США в конце XIX – начале XX в. Как ученые, так и практикующие деятели финансового рынка исходили из концепции, согласно которой экономические показатели, такие, например, как показатели погоды, являются циклическими и, соответственно, могут быть точно предсказаны. В итоге данный подход оказался неверным, однако он привел к появлению множества институтов, занимающихся сбором данных и мониторингом по финансовым рынкам, а также к конструированию экономических показателей, которые используются и по сей день и список которых постоянно расширяется с развитием мировой экономики и финансовых рынков [1].

К статистическим методам прогнозирования одномерных временных рядов принадлежат авторегрессионные модели и модели сглаживания. Авторегрессионные модели представляют текущие значения временного ряда как регрессионную зависимость от прошлых значений, а модели сглаживания считают какой-либо скользящий показатель (например, простое среднее арифметическое) и на его основании продолжают тренд [2]. Также классические модели прогнозирования могут учитывать фактор сезонности. Подобного рода модели хорошо работают при прогнозировании временных рядов с ярко выраженным трендом.

Временные ряды с выраженным трендом и с сезонностью являются нестационарными временными рядами. К стационарным временным рядам относятся ряды с постоянным средним и дисперсией. На практике такими рядами описываются случайные процессы, которые прогнозировать еще проще, достаточно посчитать среднее значение и дисперсию, тогда все фактические значения будут где-то около среднего с разбросом в среднеквадратичное отклонение [3].

Если в классической инвестиционной теории финансовые временные ряды считались случайными и стационарными [4], то начиная с 1990-х гг. этот постулат был опровергнут [5], однако на практике использование традиционных моделей Марковитца и Шарпа [6] продолжалось.

Наиболее точными на данный момент статистическими методами прогнозирования временных рядов являются модели авторегрессии – скользящего среднего (ARMA) и интегрированной авторегрессии – скользящего среднего (ARIMA) [7, с. 102]. Первая модель применима к стационарным временным рядам, а вторая приводит временной ряд к стационарному виду путем взятия разниц. Стационарность временного ряда определяется тестом Дики – Фулера и для приведения финансового ряда к стационарному виду достаточно первого порядка разностей [8].

В данной работе рассматривается не тождественное, но близкое стационарности понятие, которое традиционно применяется к финансовым временным рядам – персистентность [9, с. 69]. Персистентность в большинстве источников определяется как зависимость от прошлых значений. Таким образом, персистентные временные ряды обладают некоторой трендовостью. Понятие персистентность было введено гидрологом Гарольдом Херстом применительно к природным явлениям, а затем перенесено на финансовую сферу учеными Бенуа Мандельбротом и Эдгаром Петерсом. Автор предлагает выбирать между моделями ARMA и ARIMA, исходя не из теста Дики – Фулера, определяющего стационарность временных рядов, а по итогам R/S анализа, который показывает, персистентен или случаен временной ряд.

Цель исследования состоит в обосновании использования моделей авторегрессии – скользящего среднего и интегрированной авторегрессии – скользящего среднего для прогнозирования финансовых котировок, исходя из зависимости текущих значений временных рядов от прошлых.

Материалы и методы исследования

Модели ARMA и ARIMA

Модель ARMA (p, q) представляется следующим уравнением

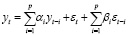, (1)

где yt – текущий уровень ряда, yt–i – уровень ряда, отстающий на i периодов, εt – случайная компонента, εt–i – случайная компонента, отстающая на i периодов, αi, βi – параметры модели [10]. Первая сумма модели является компонентой авторегрессии, а вторая – компонентой скользящего среднего. В работах автора [11, 12] было предложено в качестве ошибки рассчитывать нормально распределенный шум с нулевым математическим ожиданием и стандартным отклонением, равным стандартному отклонению ошибки прогноза по модели авторегрессии, коэффициенты которой можно рассчитать по формулам, представленным в работах Бокса и Дженкинса. Для модели ARIMA формула (1) имеет вид

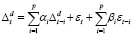, (2)

где Δd – разность порядка d.

Порядок взятия разностей определяется тестом Дики–Фуллера [13, с. 227]. Параметры p и q определяются графиками частичной автокорреляции и автокорреляции. [13, с. 223]. Коэффициенты моделей ARMA и ARIMA рассчитываются в процессе обучения модели, путем минимизации стандартного отклонения прогнозных значений ряда от фактических.

R/S анализ

R/S анализ предназначен для нахождения показателя Херста (в данном случае с целью определить персистентность временного ряда). Алгоритм осуществления R/S анализа следующий [14]. Выбирается временной ряд достаточно большого размера. Дополнительным условием выступает большое количество собственных делителей, так как от этого зависит количество подвыборок и, соответственно, объем исходных данных для построения уравнения регрессии. Частное соседних уровней ряда логарифмируется и получается ряд log(yt / yi–1) длиной n.

Находится наименьший собственный делитель n, не меньший 10 (обозначение –m). Выборка делится на k = n / m групп. Элементы в каждой группе обозначены ti В каждой группе количество элементов составляет m. Средние значения в k-й группе

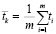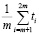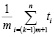, , … , , (3)

накопленные отклонения от среднего Xi:

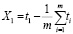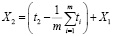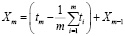, … . (4)

По каждой группе нормированный размах Rk = max(Xi) – min(Xi). Стандартное отклонение Sk по каждой группе

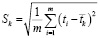. (5)

Показатель R / S по каждой группе рассчитывается как Rk / Sk. Средний размах вариации

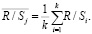(6)

Таким образом, получена выборка

, .

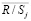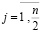Строится уравнение линейной регрессии, в котором переменной X выступает логарифм показателя R / S, а переменной Y – логарифм количества элементов в j-й группе k:

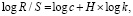(7)

где H, k – коэффициенты регрессии [15].

Автором разработан и запатентован алгоритм на Python, который позволяет рассчитать показатель Херста для различных финансовых инструментов и построить линию регрессии.

Результаты исследования и их обсуждение

Для анализа были взяты индексы AMEX, NASDAQ, NYSE американских фондовых бирж и индекс валютного рынка FOREX. Поскольку использовали данные за длительный период – 10 лет, данные по некоторым инструментам были пропущены и их пришлось отсечь. Также расчет показателя Херста потребовал более глубокой очистки данных. К примеру, для расчета показателя R/S требуется поместить стандартное отклонение в знаменатель. Таким образом, акции и валюты, котировки которых не меняются в течение длительных периодов и стандартное отклонение по ним соответственно равно нулю, отсекаются. В итоге по индексу AMEX был взят 131 инструмент, по NASDAQ – 162, по NYSE – 401, по FOREX – 338 инструментов. Из этих акций и валют выбирали те, у которых показатель Херста меньше либо равен 0,5, то есть случайные либо антиперсистентные акции.

Автором предложено выбирать модель ARMA для случайных и антиперсистентных временных рядов. Для того чтобы проверить, насколько это целесообразно, был осуществлен прогноз на годовых временных промежутках методами ARIMA и ARMA и сравнили их по метрике MAPE (средняя абсолютная ошибка в процентах). Общий период делился на тренировочный и прогнозный в соотношении 80:20. Таким образом были проанализированы котировки за 10 лет – с 2015 по 2024 г. Результаты показаны в таблице.

Из таблицы можно сделать вывод о том, что в большинстве случаев модель ARMA показывает меньшую среднюю ошибку. Только в 2018 г. по трем из двух индексов ARMA показала большую среднюю ошибку, при этом существенная разница была только по индексу AMEX. Отсюда следует вывод о том, что в первую очередь следует разделять акции по показателю Херста, а затем персистентные акции прогнозировать методом ARIMA со взятием разностей, а случайные и антиперсистентные – методом ARMA без взятия разностей. На рис. 1, 2 визуализированы прогнозы некоторых инструментов методами ARMA и ARIMA.

Усредненная по индексам MAPE (в %) по методам ARMA и ARIMA

Источник: составлено автором на основе полученных данных в ходе исследования.

а)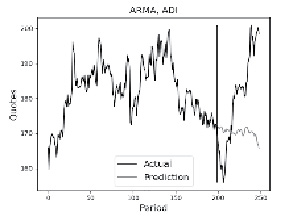

б)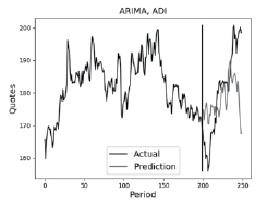

Рис. 1. Прогноз для акции Nivida методами а) ARMA, б) ARIMA Источник: составлено автором

а)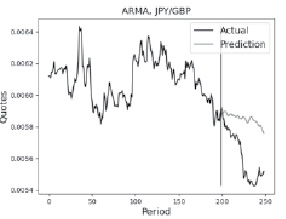

б)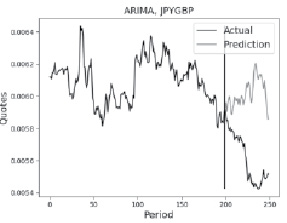

Рис. 2. Прогноз для валютной пары Японская иена / Британский фунт методами а) ARMA, б) ARIMA Источник: составлено автором

Заключение

В работе рассматривалось прогнозирование финансовых инструментов методами ARMA и ARIMA. Также автором рассмотрен показатель Херста, который позволяет делать выводы о персистентном, случайном либо антиперсистентном характере временных рядов. Нами было выдвинуто предположение о том, что случайные и антиперсистентные ряды при прогнозировании методом ARIMA не нуждаются во взятии разниц и, таким образом, модель ARIMA вырождается в модель ARMA.

С помощью разработанного автором алгоритма на языке программирования Пайтон рассчитаны показатели Херста примерно по тысяче акций и валютных пар, входящих в американские фондовые индексы и инструменты рынка FOREX. Затем выбраны те из них, у которых показатель Херста меньше либо равен 0,5, и осуществлены прогнозы по годовым выборкам за 10 периодов с 2015 по 2024 г. методами ARMA и ARIMA. По каждому методу и по каждому периоду рассчитывалась метрика MAPE, усредненная по индексу. В большинстве случаев ошибка по методу ARMA была меньше (в части случаев существенно меньше), чем по методу ARIMA, из чего можно сделать вывод о том, что использовать метод ARMA вместо ARIMA для случайных и антиперсистентных по Херсту инструментов имеет смысл.