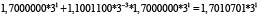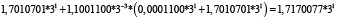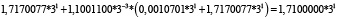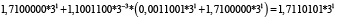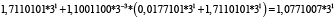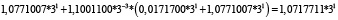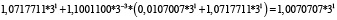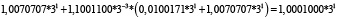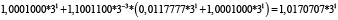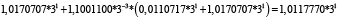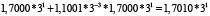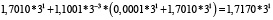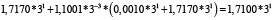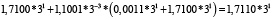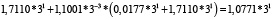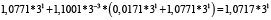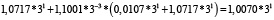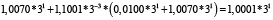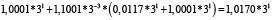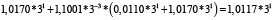Введение
Современные высокотехнологичные отрасли, такие как аэрокосмическая промышленность и ядерная энергетика, предъявляют исключительные требования к точности решения обыкновенных дифференциальных уравнений (ОДУ). В аэрокосмической сфере погрешность в 0,001 % при расчете траекторий может привести к отклонению космического аппарата на километры от цели, а в ядерной энергетике ошибка в 0,0001 % способна вызвать, перегрев активной зоны реактора. Эти примеры наглядно демонстрируют критическую важность разработки высокоточных методов численного решения ОДУ [1; 2].
В данной работе исследуется перспективный подход к повышению точности решения дифференциального уравнения классическим методом Эйлера за счет применения троично-сбалансированной системы счисления (ТСС).
Троичная сбалансированная система счисления – это позиционная система счисления, которая содержит в своем алфавите 3 символа: -1; 0; +1. Знаки перед единицами «встроены» в свои символы, и иногда разряды ТСС-чисел так и именуются – «минус/плюс». Для обозначения -1 можно использовать любой символ кроме 0 и 1, в данной работе используется символ 7 [3; 4].
Исторически первая аппаратная реализация троично-сбалансированной системы счисления была осуществлена Н.П. Брусенцовым при создании ЭВМ «Сетунь» [5]. Впоследствии данная технология получила развитие в California Polytechnic State University [6], а в настоящее время продолжает привлекать внимание разработчиков электронных систем [7].
Цель исследования – повышение точности решения дифференциальных уравнений за счет применения троичной сбалансированной системы счисления в экспоненциальном виде, с плавающей запятой.
Материалы и методы исследования
Для проведения исследований было выбрано обыкновенное дифференциальное уравнение [8; 9], решение которого осуществлялось в двоичной [10] и троичной сбалансированной системах счисления [3] с использованием классического метода Эйлера [11].
Обыкновенное дифференциальное уравнение первого порядка [12, c. 107]:
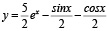 . (1)
. (1)
Формула метода Эйлера [13, c. 377]:
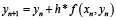 . (2)
. (2)
Результаты исследования и их обсуждение
Для удобства работы с числами в данной работе используется следующая запись числа: мантисса, со значащим разрядом до запятой – в ТСС, экспонента в десятичной системе счисления – число 3 в соответствующей степени. В табл. 1 и 2 приведены пошаговые вычисления значений дифференциального уравнения в троичной сбалансированной и десятичной системах счисления с разной степенью точности.
Таблица 1
Результаты ручного расчета ОДУ в ТСС с шагом h = 0,05, с точностью 7 трит после запятой
|
yi , i= |
Вычисление в ТСС |
Результат в десятичной СС |
|
1 |
|
2,1001371 |
|
2 |
|
2,2167352 |
|
3 |
|
2,3333333 |
|
4 |
|
2,45816188 |
|
5 |
|
2,5912208 |
|
6 |
|
2,7338820 |
|
7 |
|
2,8751714 |
|
8 |
|
3,0370370 |
|
9 |
|
3,2085048 |
|
10 |
|
3,3909465 |
Источник: составлено авторами.
Таблица 2
Результаты ручного расчета ОДУ в ТСС с h = 0,05, с точностью 4 трит после запятой
|
yi, i = |
Вычисление в ТСС |
Результат в десятичной СС |
|
1 |
|
2,111111 |
|
2 |
|
2,222222 |
|
3 |
|
2,333333 |
|
4 |
|
2,444444 |
|
5 |
|
2,592592 |
|
6 |
|
2,740740 |
|
7 |
|
2,888888 |
|
8 |
|
3,037037 |
|
9 |
|
3,222222 |
|
10 |
|
3,407407 |
Источник: составлено авторами.
В данной работе для компьютерных вычислений значений ОДУ методом Эйлера была написана программа на языке Си, использующая для переменных стандартный 32-битный формат данных IEEE 754 с плавающей запятой: бит 31 – знак мантиссы, 30 – 23 биты – экспонента, 22 – 0 биты – мантисса без первой цифры, что обеспечивает примерно 7 десятичных значащих цифр в диапазоне ±8388608. Особое внимание уделялось изучению влияния точности представления чисел на накопление вычислительной погрешности – проводились серии расчетов с последовательным уменьшением разрядности мантиссы как для исходных данных, так и для промежуточных результатов.
Запись аналитического решения ОДУ [14; 15], а также результаты решения ОДУ классическим методом Эйлера в двоичной системе счисления, в случае, если задействованы все 23 бита при представлении мантиссы, изображены на рис. 1.
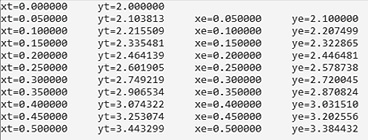
Рис. 1. Результаты решения ОДУ аналитическим (yt) и численным методом (ye) в компьютерном представлении в виде короткого вещественного числа
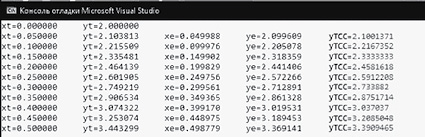
Рис. 2. Результаты решения ОДУ аналитическим (yt) и численным (ye) методами представлены в виде вещественных чисел с усеченной 10-битной мантиссой
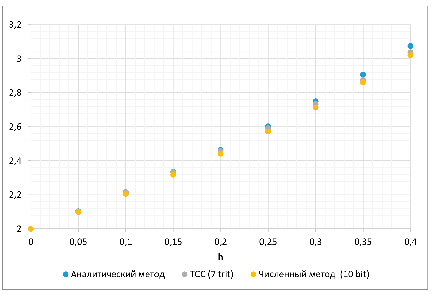
Рис. 3. Графическое представление результатов решения ОДУ
После усечения разрядов до 10 бит представления мантиссы, значащая часть числа находится в диапазоне ±1024 (десятичное представление), мантисса в 7 трит ТСС числа соответствует диапазону ±1093 (десятичное представление). Запись аналитического решения ОДУ, а также результаты компьютерного решения ОДУ классическим методом Эйлера приведены на рис. 2.
Точечная диаграмма результатов решения ОДУ приведена на рис. 3.
После усечения разрядов до 5 бит представления мантиссы, значащая часть числа находится в диапазоне ±32 (десятичное представление), мантисса в 4 трита ТСС числа соответствует диапазону ±40 (десятичное представление). Запись аналитического решения ОДУ, а также результаты решения ОДУ классическим методом Эйлера в двоичной системе счисления при шаге h = 0,05 приведены на рис. 4.
Точечная диаграмма результатов решения ОДУ приведена на рис. 5.
Как видно из рис. 3 и 5, результат решения ОДУ классическим методом Эйлера с применением ТСС позволяет получить более точное решение по сравнению с традиционной двоичной реализацией.
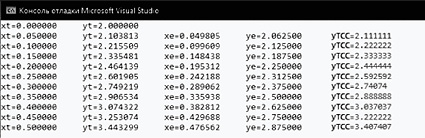
Рис. 4. Результаты решения ОДУ аналитическим (yt) и численным (ye) методами представлены в виде вещественных чисел с усеченной 5-битной мантиссой
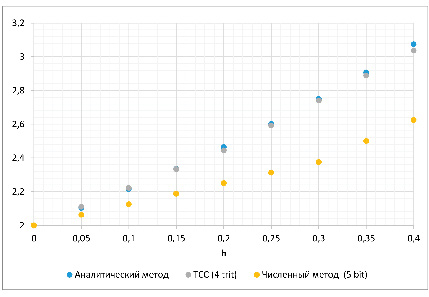
Рис. 5. Графическое представление результатов решения ОДУ
Заключение
Исследование показало высокую эффективность троично-сбалансированной системы счисления (ТСС) для решения дифференциальных уравнений методом Эйлера, погрешность вычислений в рамках проведенных исследований составляла 1–6 %.
Применение ТСС в классическом методе Эйлера на примере обыкновенного дифференциального уравнения позволило достичь значительного улучшения точности вычисления – в 5 раз и более раз по сравнению с традиционной двоичной реализацией.