Введение
При обработке статистических данных на практике довольно часто возникает ситуация, когда исследуемая переменная носит категориальный или качественный характер [1; 2]. Например, к категориальной переменной [3] относится «пол человека», «группа крови», «тип заболевания», «страна», «политическая партия» и т.д. Для включения таких категориальных переменных в регрессионную модель их предварительно маркируют (кодируют), то есть присваивают каждой категории уникальное целое значение. Если порядок категории важен, то переменную называют порядковой, а если нет – номинальной. Существует множество методов кодирования категориальных переменных (например, [4–6]). Так, в работе Д.В. Новиковой сравнивается эффективность следующих методов: порядковое, горячее, бинарное, восьмеричное, частотное и целевое кодирование, а также кодирование Стейна, Гельмерта и метод обратной разницы [6].
Аппарат математического программирования уже много десятилетий используется в рамках регрессионного анализа. Основой для этого послужила работа Х.М. Вагнера, в которой задача оценки неизвестных параметров линейной регрессии с помощью метода наименьших модулей (МНМ) была сведена к задаче линейного программирования [7]. К настоящему времени в регрессионном анализе появилось несколько новых разновидностей регрессионных моделей, оценка параметров которых с помощью МНМ предполагает решение задач частично булевого линейного программирования (ЧБЛП). Сегодня эффективность решателей таких задач, как отмечено в работе Т. Коха, Т. Бертхолда, Я. Педерсена и Ч. Ванарета, заметно повысилась [8]. Так, в работе С.И. Носкова задача оценки параметров производственной функции Леонтьева с помощью МНМ сведена к задаче ЧБЛП [9, с. 120–121]. В статье [10] введены модульные регрессии, которые послужили фундаментом для разработки их многослойного аналога [11] и «широкой» модульной регрессии [12]. В работе [13] автором описана задача оценки параметров регрессионных моделей с целочисленными функциями пол и потолок с применением аппарата частично целочисленного линейного программирования (ЧЦЛП). Такие модели целесообразно строить, когда зависимая переменная принимает целые значения. Следовательно, такие регрессии отлично подходят для ситуаций, когда зависимая переменная носит категориальный характер. Проблема состоит в том, каким образом следует маркировать зависимую переменную, чтобы качество регрессии с выбранной целочисленной функцией было наилучшим.
Цель исследования состоит в формализации задачи ЧЦЛП для идентификации с помощью МНМ параметров регрессионной модели с целочисленной функцией пол с одновременной маркировкой значений зависимой переменной.
Материалы и методы исследования
Для оценки параметров регрессионных моделей применяется МНМ, реализуемый в виде задачи линейного программирования. Интеграция функции пол в эту задачу производится с помощью целочисленных переменных.
Результаты исследования и их обсуждение
Пусть исследуется влияние l объясняющих (независимых) переменных x1, x2, …, xl на объясняемую (зависимую) переменную y. Предположим, что объясняющие переменные имеют значения xij, 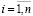 ,
, 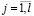 , где n – объем выборки.
, где n – объем выборки.
Допустим, что зависимая переменная y имеет категориальный характер.
Будем считать, что число категорий равно p. Тогда значения переменной y можно промаркировать, например, следующим образом:
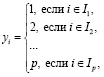 (1)
(1)
где Ik – множество номеров наблюдений, относящихся к k-й категории. Очевидно, что справедливы следующие соотношения между этими множествами:
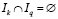 ,
, 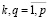 , k ≠ q,
, k ≠ q,
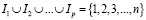 .
.
Выражение (1) означает, что маркером для первой категории переменной y выступает целое число 1, маркером для второй категории – целое число 2, и т.д. Тогда для исследования зависимости y от x1, x2, …, xl целесообразно использовать предложенную в [13] регрессионную модель с целочисленной функцией пол:
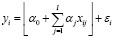 ,
, 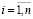 , (2)
, (2)
где α0, α1, …, αl – неизвестные параметры; εi, 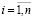 – ошибки регрессии; скобками
– ошибки регрессии; скобками 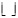 обозначена рассмотренная в работе Р. Грэхема, Д. Кнута и О. Паташника целочисленная функция пол, которая округляет заключенное в них значение до ближайшего целого числа в меньшую сторону [14, с. 88]. Например,
обозначена рассмотренная в работе Р. Грэхема, Д. Кнута и О. Паташника целочисленная функция пол, которая округляет заключенное в них значение до ближайшего целого числа в меньшую сторону [14, с. 88]. Например, 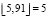 .
.
Модель (2) относится к классу нелинейных регрессий. Для оценки ее неизвестных параметров с помощью МНМ требуется решить задачу:
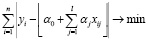 . (3)
. (3)
В работе автора [13] показано, что решение задачи (3) сводится к решению задачи ЧЦЛП. Учитывая, что зависимая переменная по правилу (1) принимает ограниченное множество значений, такая задача будет иметь следующий вид:
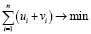 , (4)
, (4)
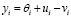 ,
, 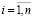 , (5)
, (5)
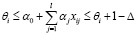 ,
, 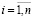 , (6)
, (6)
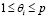 ,
, 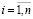 (7)
(7)
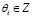 ,
, 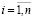 , (8)
, (8)
ui ≥ 0, vi ≥ 0, 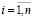 , (9)
, (9)
где Z – множество целых чисел; если ошибка регрессии в i-м наблюдении положительна, то ее модуль численно равен значению переменной ui, а если отрицательна, то значению переменной vi, причем, ui ∙ vi = 0 для любого i; θi – предсказанный по модели маркер (категория) зависимой переменной в i-м наблюдении; Δ – выбранное исследователем близкое к нулю положительное число.
Задача ЧЦЛП (4)–(9) подходит для моделирования порядковой категориальной зависимой переменной y, маркировка которой производится по правилу (1). Например, как отмечено в работе С. Баладрам, такой порядковой переменной может служить «температура», принимающая значения «очень низкая», «низкая», «высокая» и «очень высокая» [3]. Отметим, что в таком случае маркировать значения зависимой переменной y можно не только целыми числами в диапазоне от 1 до p, но и в любом диапазоне от (1+k) до (p+k), где k – целое число. Действительно, пусть задача (4)–(9), в которой переменная y закодирована по правилу (1), имеет оптимальное решение 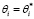 ,
, 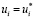 ,
, 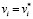 ,
, 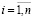 ,
, 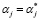 ,
, 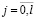 . Промаркируем теперь зависимую переменную y по правилу
. Промаркируем теперь зависимую переменную y по правилу
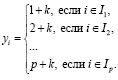 (10)
(10)
И рассмотрим задачу (4)–(9), в которой линейные ограничения (7) заменены на двойные неравенства 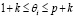 ,
, 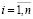 . Очевидно, что эта задача будет иметь оптимальное решение
. Очевидно, что эта задача будет иметь оптимальное решение 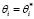 ,
, 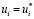 ,
, 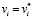 ,
, 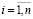 ,
, 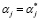 ,
, 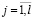 ,
, 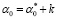 . Таким образом, при маркировке зависимой переменной y по правилу (10) для любого k оптимальные значения всех параметров, кроме α0, сохраняются.
. Таким образом, при маркировке зависимой переменной y по правилу (10) для любого k оптимальные значения всех параметров, кроме α0, сохраняются.
Рассмотрим теперь ситуацию, когда категориальная зависимая переменная y носит номинальный характер. Такой переменной может служить, например, «прогноз погоды», категории которой «солнечно», «пасмурно» и «дождливо» [3]. Порядок маркировки этих категорий не важен. Иными словами, категории «солнечно» можно присвоить число 1, «пасмурно» – 2, «дождливо» – 3. Либо категории «солнечно» можно поставить в соответствие число 2, «пасмурно» – 3, «дождливо» – 1. Естественно, что выбранное правило маркировки значений зависимой переменной y будет влиять на решение задачи (4)–(9). Это доказывается на примере в следующем разделе статьи.
Возникает задача выбора оптимальной маркировки значений зависимой переменной y наряду с идентификацией неизвестных параметров регрессионной модели (2) с помощью МНМ. Введем следующее правило маркировки значений категориальной переменной y:
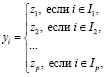 (11)
(11)
где z1, z2, …, zp – маркеры каждой категории переменной y, принимающие целые и отличные друг от друга значения из диапазона от 1 до p.
Введем булевы переменные σqk, 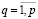 ,
, 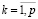 по следующему правилу:
по следующему правилу:
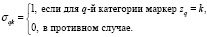
В задачу математического программирования ограничения на булевы переменные интегрируются в виде
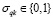 ,
, 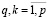 . (12)
. (12)
Тогда выбор маркера для первой категории реализуется через следующее линейное ограничение:
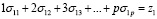 .
.
Если в этом ограничении, например, σ13 = 1, а все оставшиеся булевы переменные равны 0, то маркер z1 принимает значение 3. В общем виде все маркеры zp, 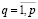 связаны с булевыми переменными равенствами
связаны с булевыми переменными равенствами
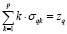 ,
, 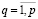 . (13)
. (13)
Для обеспечения выбора только одного маркера для каждой категории требуется ввести ограничения
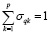 ,
, 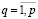 , (14)
, (14)
а для обеспечения различия маркеров из разных категорий – ограничения
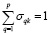 ,
, 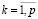 . (15)
. (15)
Вместо фиксированных значений маркеров yi в (5) с учетом правила (11) используем переменные zq:
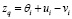 ,
, 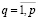 ,
, 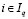 . (16)
. (16)
Тогда решение задачи ЧЦЛП с целевой функцией (4) и с линейными ограничениями (6)–(9), (12)–(16) дает оптимальные по МНМ значения параметров θi, ui, vi, 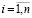 , αj,
, αj, 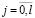 , σqk,
, σqk, 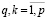 , zq,
, zq, 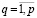 .
.
Для проведения вычислительных экспериментов была использована известная выборка данных, содержащая информацию о биологических видах животных [15]. Объем выборки составляет 101 наблюдение. Зависимая переменная y является категориальной и выражает категорию (класс, тип) животного. Всего представлено 7 категорий. К первой относится 41 вид (медведь, слон, жираф, заяц, волк и пр.). Ко второй – 20 видов (курица, утка, страус и пр.). К третьей – 5 видов (морская змея, черепаха и пр.). К четвертой – 13 видов (окунь, карп, щука, пиранья и пр.). К пятой – 3 вида (лягушка, тритон и жаба). К шестой – 8 видов (комар, пчела, муха и пр.). К седьмой – 10 видов (краб, рак, осьминог, скорпион и пр.). По умолчанию каждой категории был присвоен соответствующий ей номер, то есть zq = q, 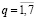 . Категория животного предсказывается 15 бинарными переменными: x1 – волосы; x2 – перья, x3 – яйца, x4 – молоко, x5 – воздушное, x6 – водное, x7 – хищник, x8 – зубастое, x9 – позвоночник, x10 – дышащее, x11 – ядовитое, x12 – плавники, x14 – хвост, x15 – домашнее, x16 – кошачий. И одна объясняющая переменная x13 – число лап, которая принимает целые значения 0, 2, 4, 5, 6 и 8.
. Категория животного предсказывается 15 бинарными переменными: x1 – волосы; x2 – перья, x3 – яйца, x4 – молоко, x5 – воздушное, x6 – водное, x7 – хищник, x8 – зубастое, x9 – позвоночник, x10 – дышащее, x11 – ядовитое, x12 – плавники, x14 – хвост, x15 – домашнее, x16 – кошачий. И одна объясняющая переменная x13 – число лап, которая принимает целые значения 0, 2, 4, 5, 6 и 8.
Предварительно общий список из 16 объясняющих переменных был сокращен до 3 наиболее сильно влияющих на y переменных – x4, x9 и x10. Для их выбора применен метод последовательного исключения, алгоритм которого встроен в пакет Gretl, с использованием двухстороннего p-значения 0,01. Построенная по этим переменным с помощью МНМ линейная регрессия имеет уравнение
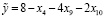 . (17)
. (17)
Для модели (17) сумма модулей ошибок (SAE) составила 27.
Построенная модель (2) с целочисленной функцией пол имеет вид
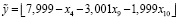 . (18)
. (18)
Для регрессии (18) SAE = 20, то есть ее качество выше, чем у модели множественной линейной регрессии (17).
Сначала маркировка категориальной переменной y проводилась вручную. В первый раз категориям случайно были присвоены маркеры z1 = 3, z2 = 6, z3 = 1, z4 = 7, z5 = 2, z6 = 5, z7 = 4. Решение задачи ЧЦЛП (4)–(9) позволило идентифицировать модель
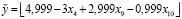 , (19)
, (19)
для которой SAE = 50.
Во второй раз категориям случайно были присвоены значения z1 = 1, z2 = 5, z3 = 4, z4 = 7, z5 = 6, z6 = 2, z7 = 3. В результате была построена модель
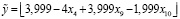 ,(20)
,(20)
для которой SAE = 14.
Как видно, при разной маркировке категориальной переменной качество регрессионной модели (2) меняется. Так, регрессия (19) оказалась хуже модели (18) с кодами категорий по умолчанию, а регрессия (20) лучше, чем (18).
После чего решалась задача ЧЦЛП (4), (6)–(9), (12)–(16). В ограничениях (6) число Δ = 0,0001. В результате была построена модель
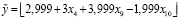 , (21)
, (21)
для которой SAE = 12. При этом оптимальные маркеры категорий переменной y оказались следующими: z1 = 7, z2 = 4, z3 = 5, z4 = 6, z5 = 3, z6 = 1, z7 = 2. Как видно, модель (21) превосходит по качеству все построенные регрессии (17)–(20). Значение SAE = 12 означает, что только в 12 наблюдениях из 101 тип животного был классифицирован неверно. Это наблюдения под номерами 26, 27, 53, 63, 73, 77, 81, 82, 90, 91, 92 и 100.
Заключение
В результате проведенных исследований задача одновременной идентификации с помощью МНМ и маркеров категориальной переменной y, и параметров регрессионной модели с целочисленной функцией пол сведена к задаче ЧЦЛП. На примере решения задачи классификации видов животных доказана корректность разработанного математического аппарата. Построенная предложенным способом регрессионная модель превзошла по качеству регрессии, оцененные по известным алгоритмам. В дальнейшем планируется использовать полученные результаты для модернизации метода оценки списочных регрессионных моделей.



