Введение
Подготовка квалифицированных кадров является стратегической целью государственной политики в области российского высшего образования, достижение которой определяет технологический и экономический суверенитет страны. Министерство науки и высшего образования России в качестве одной из перспективных задач на среднесрочный период рассматривает обеспечение доступности высшего образования [1, с. 178]. Для вузов решение этой задачи предполагает, в частности, сохранение контингента студентов за счет повышения успешности их обучения. Это позволит не только повысить качество подготовки специалистов, но и обеспечить стабильное финансирование образовательной организации.
В связи с этим является актуальной проблема оценки эффективности основных профессиональных образовательных программ (ОПОП), основанная на прогнозировании успешности обучения студентов. Анализ литературы показал, что обозначенная проблема является важной не только в России, но и за рубежом. Несмотря на довольно обширный опыт по созданию прогностических систем в иностранных университетах (Висконсинский университет (США), университет Пердью (США), Миланский политехнический университет (Италия), Мадридский университет UDIMA (Испания) и др.), следует согласиться, что прямое заимствование зарубежного опыта учебной аналитики нецелесообразно за счет существенных отличий российской системы образования [2].
Немногочисленные исследования российских ученых в области научного прогнозирования успешности обучения отличаются подходами к выбору предмета и методов исследования. При этом понятие «успешность обучения» в исследованиях, основанных на применении количественных методов, трактуется по-разному. Во всех проанализированных источниках определения данного понятия связаны с академической успеваемостью студентов: успешность обучения как положительная итоговая оценка по определенной учебной дисциплине [3], доля успешно сдавших сессию обучающихся [4], обучение, демонстрирующее положительную динамику успеваемости по совокупности учебных дисциплин [5].
При построении прогностических моделей успешности обучения, как правило, исследователи используют данные образовательного профиля обучающегося на платформе электронного обучения вуза. При этом применяются различные методы моделирования. В исследовании Р.В. Есина и соавторов используются дерево решений и моделирование на основе логистической регрессии [2]. Г.П. Озерова, Г.Ф. Павленко использовали методы машинного обучения [6]. М.В. Носков с соавторами и С.В. Помян с соавторами построили прогностические модели на основе марковских процессов [7, 8]. В исследовании С.В. Щербина и соавторов применяются методы кластерного и регрессионного анализа [9]. В исследовании В.И. Токтаровой и соавторов построение моделей осуществляется с использованием технологий искусственного интеллекта [10].
Успешность освоения ОПОП зависит не только от обучающихся, но и от содержания и условий реализации программы. В исследовании А.Н. Сергеева эффективность реализации ОПОП понимается как показатель, отражающий количество привлекаемых ресурсов для полноценной реализации всех видов учебной работы, предусмотренных учебным планом [11]. В исследовании Т.В. Зыковой и соавторов представлена методика анализа учебного плана, позволяющая судить о качестве педагогического дизайна ОПОП с точки зрения достижения сформированности у обучающихся необходимых компетенций [12].
В условиях конкуренции вузов все субъекты системы образования должны иметь возможность оценить эффективность предлагаемых ОПОП, в том числе с точки зрения возможностей их успешного освоения.
Цель исследования – разработать методику оценки эффективности ОПОП на основе вероятностей успешного обучения. Под успешным обучением в настоящем исследовании понимается получение обучающимися положительных оценок, превышающих заданный уровень, по всем дисциплинам учебного плана ОПОП. Достижение поставленной цели предполагает последовательное решение следующих задач:
− преобразовать оценки (от 60 до 100 баллов) по учебным дисциплинам ОПОП в случайные величины, распределенные на отрезке [0;1];
− построить модели одномерных распределений, оценить их параметры и проверить адекватность;
− построить модели совместного распределения (для двумерных и многомерных случайных величин);
− вычислить вероятности успешного обучения на основе построенной модели.
Материалы и методы исследования
В работе был применен комплекс теоретических и эмпирических методов исследования. На основе сравнительно-сопоставительного анализа научной литературы были выявлены существующие подходы к решению проблемы прогнозирования успешности обучения и оценки эффективности образовательных программ. Для проведения эмпирического исследования были использованы данные промежуточной аттестации 22 студентов по всем дисциплинам учебного плана, обучавшихся одновременно в Астраханском государственном университете имени В.Н. Татищева по направлению подготовки 44.03.05 Педагогическое образование (с двумя профилями подготовки «Математика и информатика») с 2019 по 2024 гг. По этим данным была построена модель совместного распределения успеваемостей по всем дисциплинам образовательной программы с применением моделей бета-распределения одномерных случайных величин, копул Гамбела–Хаугарда для распределений двумерных случайных величин и иерархической копулярной модели для многомерного распределения. Построенная модель позволяет найти вероятности успешного обучения. Обработка данных выполнялась в статистическом пакете R.
Результаты исследования и их обсуждение
В качестве исходных данных использованы результаты обучения группы студентов по всем дисциплинам основной профессиональной образовательной программы по направлению подготовки 44.03.05 Педагогическое образование (с двумя профилями подготовки «Математика и информатика»). Результаты обучения оценивались в баллах по 100-балльной шкале. Оценке «удовлетворительно» соответствуют баллы от 60 до 69, оценке «хорошо» – от 70 до 89, оценке «отлично» – от 90 до 100. Некоторые дисциплины изучаются несколько семестров. В этом случае каждый ряд оценок по семестрам учитывался отдельно. В итоге получилось 103 ряда оценок.
юбые оценки в баллах являются порядковыми (ранговыми) случайными величинами. Однако, если размах колебаний является достаточно большим по сравнению с ценой деления балльной шкалы, приближенно можно считать баллы количественными случайными величинами. Баллы варьируются от 60 до 100, что позволяет считать их количественными случайными величинами. Предварительно баллы вычитались из 100 и полученный результат делился на 40. Полученные таким способом случайные величины далее будем называть переменными и обозначать xi.
Для моделирования одномерных распределений случайных величин xi было использовано бета-распределение, плотность которого равна нулю вне отрезка [0;1], а для х ∈ [0; 1] имеет вид [13]:
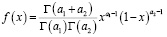 . (1)
. (1)
Параметры бета-распределения вычислялись методом моментов. При этом теоретические моменты, зависящие от параметров распределения, приравниваются к выборочным моментам [13]:
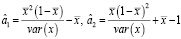 . (2)
. (2)
Полученные оценки параметров бета-распределения для всех рядов преобразованных оценок по учебным дисциплинам представлены на разработанном авторами сайте (https://676.su/alit). Для решения вопроса о приемлемости бета-распределения был выполнен тест Колмогорова–Смирнова. В результате оказалось, что бета-распределение не подходит для рядов оценок по 20 учебным дисциплинам из 103. В случаях когда бета-распределение оказалось неприменимым, преподаватель, как правило, придерживался своеобразного подхода к оцениванию знаний студентов.
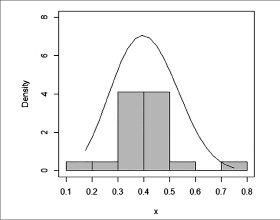
Рис. 1. Гистограмма оценок по дисциплине «Информатика» с графиком соответствующего бета-распределения Источник: составлено авторами
Например, по одной из учебных дисциплин преподаватель выставил студентам только два вида оценок: 60 или 90 баллов. Поэтому для дальнейшего исследования были использованы ряды оценок xi только по 83 дисциплинам. Для каждой переменной xi был вычислен ряд значений uk (k = 1,…,83) соответствующей функции распределения. Пример модели одномерного распределения оценок для дисциплины «Информатика» (оценки параметров бета-распределения 6,56 и 9,47, p-value 0,605), приведенный на рисунке 1, визуализирует возможность использования бета-распределения для моделирования этого одномерного распределения.
В настоящее время для моделирования совместных распределений случайных величин хорошо себя зарекомендовали копула-функции. Копулой называется функция совместного распределения нескольких случайных величин, каждая из которых имеет равномерное распределение на отрезке [0;1]. Распространенным является подход, когда сначала моделируют парные распределения, а затем из них строят более сложные модели по определенному алгоритму [13].
Для моделирования парных распределений зависимостей между переменными uk в настоящем исследовании была выбрана копула Гамбела–Хаугарда [13]:
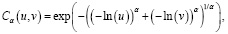 (3)
(3)
где u, v – случайные величины, a – параметр, подлежащий оценке по исходным данным.
Выбор копулы Гамбела–Хаугарда обусловлен тем, что она часто используется в экономических исследованиях [14], достаточно просто устроена и ее параметр a просто связан с коэффициентом τ ранговой корреляции Кендалла [13]:
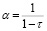 (4)
(4)
Коэффициент τ был вычислен для пар рядов uk с помощью программы R.
Иерархическая копулярная модель для многомерного распределения строилась следующим образом. Среди рядов значений функций распределения uk (k = 1, … , 83) выбиралась пара рядов, для которых коэффициент корреляции τ был наибольшим. Для этого авторами была создана в R специальная функция taumax. Код и результат работы этой функции представлены на рисунке 2.
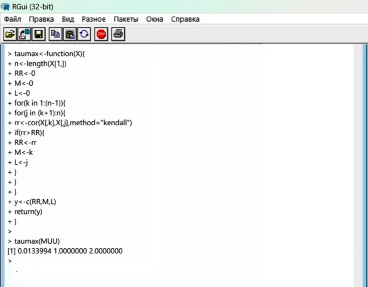
Рис. 2. Функция выбора пары рядов с наибольшим коэффициентом корреляции Кендалла Источник: составлено авторами
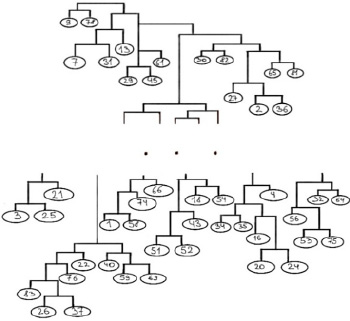
Рис. 3. Фрагмент структуры иерархической копулярной модели Источник: составлено авторами
Вероятности успешного обучения
|
Событие |
Вероятность по копулярной модели |
Вероятность при условии независимости |
Относительная частота |
|
А |
0,0197086 |
1,443258*10-9 |
0,091 |
|
Б |
4,252882*10-5 |
2,429692*10-25 |
0 |
|
С |
0,0001410377 |
4,13788*10-22 |
0 |
Примечание: составлено авторами.
На первом шаге такими рядами оказались ряды, соответствующие дисциплинам «Теоретико-групповые принципы геометрии» и «Практикум по решению математических задач». Два данных ряда заменялись рядом функции совместного распределения по формуле (3). Затем указанный процесс для пар рядов с наибольшим коэффициентом корреляции повторялся до тех пор, пока не остался один ряд. Соответствующий алгоритм, а также результат его применения размещены на сайте авторов (https://676.su/alit). Фрагмент структуры иерархической копулярной модели изображен на рисунке 3.
Построенная модель позволяет вычислять вероятности успешного обучения на исследуемой ОПОП (https://676.su/alit). Были вычислены вероятности трех случайных событий: А – выпускник образовательной программы завершил его «без троек», т.е. все его оценки не менее 70 баллов; B – все оценки выпускника не менее 80 баллов. В третьем случае все учебные дисциплины были разбиты на три модуля: модуль профессиональной подготовки, модуль психолого-педагогической подготовки и модуль общей культурной подготовки. Событие С – выпускник получил оценки не ниже 80 баллов по всем дисциплинам профессионального модуля, оценки не ниже 70 баллов по всем дисциплинам психолого-педагогического модуля и оценки не ниже 60 баллов по остальным дисциплинам.
Для сравнения были определены относительные частоты этих событий по данной выборке, а также вероятности этих событий в предположении о независимости оценок. Результаты представлены в таблице.
В результате вероятность закончить обучение по рассматриваемой ОПОП «без троек» составила примерно 0,02, т.е. закончить обучение без троек может только 1 студент из 50. В исследуемой выборке таких студентов оказалось 2 из 22. Такое расхождение можно объяснить с двух точек зрения. Это может быть как следствием несовершенства модели, так и следствием случайного стечения факторов. Вероятность закончить обучение по исследуемой ОПОП, получив по всем дисциплинам оценки не ниже 80 баллов, не нулевая. Однако в данной выборке таких студентов нет. Вероятности рассмотренных случайных событий А, В и С, вычисленные с использованием иерархической копулярной модели совместного распределения, оказались значительно выше вероятностей, вычисленных в предположении независимости оценок по различным дисциплинам. Можно признать результат моделирования достаточно успешным.
Заключение
Построенная совокупность моделей позволяет прогнозировать успешность обучения по ОПОП в соответствии с заданным уровнем успеваемости студентов. При построении модели совместного распределения многомерной случайной величины вместо копулы Гамбела–Хаугарда можно использовать и другие копулярные модели. Сравнение этих моделей и поиск наилучшей могут составить предмет дальнейшего развития системы оценки эффективности основных профессиональных образовательных программ.
Разработанная авторами методика оценки эффективности образовательных программ на основе вероятностей успешного обучения может стать одной из основных для сравнения двух ОПОП по родственным направлениям подготовки. При этом программа, для которой вероятность успешного обучения окажется выше, может считаться более эффективной.



