Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Введение

Исследования в области механической обработки сосредоточены на двух аспектах: первый касается технологических разработок, направленных на повышение производительности и качества готовых деталей, второй – моделирование, которое используется для прогнозирования сил резания, температурных полей и свойств готовых поверхностей. На современном этапе развития технологий проектирования эффективность работы металлорежущего оборудования во многом зависит от свойств и стабильности свойств материалов режущего инструмента, заготовки, характеристик других элементов технологической системы [1-3].

Изучение физических явлений, сопровождающих процессы механической лезвийной обработки и, соответственно, изучение закономерностей формирования свойств обработанной поверхности, традиционно проводится [3, 4] на примере токарной обработки. Такой подход был принят, поскольку, во-первых, однолезвийное точение «избавлено» от комплекса усложняющих взаимодействий [5-7], связанных с одновременной работой нескольких режущих лезвий или сложностью геометрической формы обрабатываемой поверхности. Во-вторых, токарная обработка до настоящего времени остается наиболее распространенным [6, 8] методом механической лезвийной обработки.

Моделирование результатов обработки проведено на примере углеродистой стали C1018 (сталь 20 по ГОСТ 1050-2013). В процессе токарной обработки основные причины шероховатости поверхности связаны с тремя аспектами: геометрическими и физическими [6, 7] причинами и изменениями условий резания [5, 8] в процессе обработки. Рассмотрены три спецификации регрессионных моделей [9], наиболее часто применяемые в инженерном проектировании:

линейная 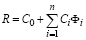; (1)

степенная 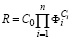; (2)

показательная 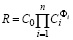; (3)

где R – функция отклика; в данной работе в качестве функции отклика рассматривается среднее арифметическое отклонение высоты микронеровностей Ra;

Ci – коэффициенты регрессионной модели;

Ci > 0 – зависимость возрастающая, при увеличении значения фактора значение функции увеличивается;

Ci < 0 – зависимость убывающая, при увеличении значения фактора значение функции уменьшается;

Ci ≈ 0 – зависимость отсутствует, аргумент не оказывает влияния на функцию;

Φi – независимые переменные многофакторной регрессионной модели (факторы): технологические условия обработки: скорость резания V, глубина резания t и скорость продольной подачи S, предположительно оказывающие влияние на формирование качества поверхности;

n, i – соответственно количество и текущий номер рассматриваемых факторов.

Входные факторы должны удовлетворять условию взаимной независимости [9], что формально проверяется по величине абсолютного значения коэффициентов парной корреляции (табл. 1) «фактор – фактор» – величина коэффициента должна быть малой.

Помимо независимых факторов, названных выше, в регрессионных моделях учтено влияние взаимодействий [9] – рассмотрены псевдофакторы, образованные попарными сочетаниями независимых объясняющих переменных [10].

Таблица 1

Коэффициенты парной корреляции

Цель исследования – выделение группы наиболее значимых по степени влияния на шероховатость технологических условий обработки, определяющих закономерности и результаты формирования микрорельефа обработанной поверхности.

Материалы и методы исследования

Теория регрессионного анализа позволяет анализировать и оценивать данные, полученные в результате моделирования. Функция отклика дает возможность качественно сравнить коэффициенты регрессии объясняющих факторов, затем выявить их влияние и, наконец, лучше понять закономерности в процессе формирования высоты микрорельефа обработанной поверхности Ra. Эта теория использована для анализа и оценки факторов, участвующих в процессе механической однолезвийной обработки [11, 12].

С учетом результатов, полученных ранее [5-7], сделано допущение о нелинейном характере зависимости высоты микронеровностей от технологических условий обработки. С учетом такого допущения план исследований для построения модели включает эксперименты [13, 14, 15] с тремя уровнями вариации факторов. Нормированные значения переменных модели равны [–1; 0; +1]. Реальные значения соответствующих физических величин при проведении определяются нормирующими соотношениями. Минимальное количество экспериментов, проведенных при различных неповторяющихся сочетаниях условий обработки, необходимое для построения модели [9, 11], составляет для трех независимых факторов V, S, t: 33 = 27.

Условия обработки – продольное наружное чистовое точение заготовок из холоднокатаной углеродистой стали C1018. Глубина резания t = 0,5…0,7 мм, двухкарбидный твердый сплав Т15К6. Геометрия режущей части инструмента:

γ = 0°, α = α1 = 10°, ф = 45°,

ф1, = 25°, r = 0,3…0,4 мм.

Результаты исследования и их обсуждение

Регрессионный анализ проводится в форме статистического исследования результатов эксперимента. Целью регрессионного анализа является определение перечня технологических факторов и их взаимодействий, оказывающих статистически значимое влияние на шероховатость поверхности (Ra). Критерии выбора модели, обеспечивающей наиболее качественное [11] описание процесса: стандартное отклонение; средняя относительная погрешность; F-критерий Фишера; оценка адекватности модели – вероятность существования выявленной зависимости.

В таблице 2 приведен план проведения экспериментальных исследований [8]. Условия резания, используемые для испытаний, изменяются в следующих диапазонах: V = [50–120] м/мин; S = [0,08–0,16] мм/об; t = [0,5–0,7] мм.

Функциональная связь между входными параметрами (V, S и t) и выходными параметрами (Ra), определяемыми как параметры технологической обработки, называется регрессией. Отметим, что для обеспечения корректности регрессионного моделирования необходимо, чтобы для переменных величин, входящих в модель, выполнялся комплекс условий [9, 11] Гаусса–Маркова. Для обеспечения этих условий производится операция нормирования [11]. Способ нормирования определяется спецификацией исходной модели.

В результате нормирования математические зависимости (1), (2), (3) рассматриваемых спецификаций принимают линейный вид (4).

линейная 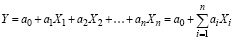(4)

где Y – функция отклика нормированной модели;

Xi – независимые переменные нормированной модели;

ai – коэффициенты регрессии нормированной модели (рис. 1); численные значения коэффициентов регрессии нормированной модели равны частным производным 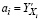нормированной функции отклика по соответствующим независимым переменным нормированной модели (4).

Таблица 2

Фрагмент массива исходных данных в размерном и нормированном виде

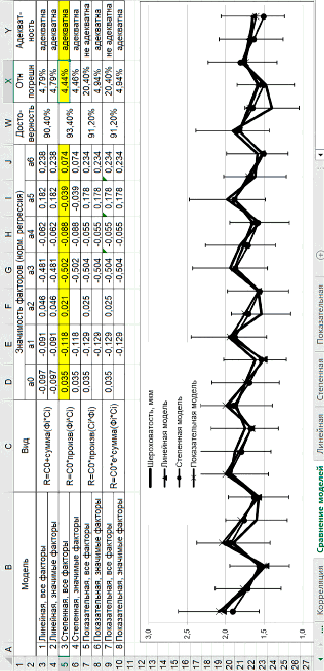
Рис. 1. Рабочий лист «Сравнение моделей»

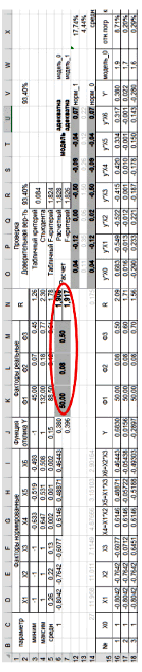
Рис. 2. Рабочий лист «Степенная»

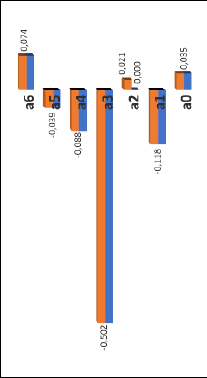
Рис. 3. Сравнение значимости технологических условий обработки

Поскольку все переменные нормированной модели имеют одинаковый численный масштаб и являются безразмерными математическими величинами, для независимых переменных допустима операция оценки сравнительной значимости соответствующих технологических факторов процесса на функцию отклика по величине коэффициентов регрессии нормированной модели.

Пример расчета коэффициентов ai показан на рисунке 2.

Анализ данных, представленных на рисунках 1, 2, позволяет сделать следующие выводы. Средняя относительная погрешность показательной модели превышает аналогичные параметры линейной и степенной (12,67% – показательная; 4,79% – линейная; 4,45% – степенная). Максимальная относительная погрешность модели составляет около 17%, а средняя относительная погрешность – 4%.

В контексте обсуждаемой модели значимость фактора относится к его статистической значимости в пределах интервалов варьирования переменных исходной модели. Это означает, что факторы, которые были определены как значимые, оказывают влияние на результаты модели, в то время как незначимые факторы могут быть исключены из анализа без потери важной информации. Важность того или иного фактора оценивается путем определения коэффициентов регрессии. Они могут принимать положительные или отрицательные значения, указывая на направление их влияния. Гистограмма на рисунке 3 показывает значения коэффициентов регрессии a0, a1, a2, a3, a4, a5 и a6 для изучаемой линейной модели.

В электронной таблице для степенной модели на рисунке 2 представлены коэффициенты регрессии 0,04, –0,12, 0,02, –0,50, –0,09, –0,04 и 0,7. Эти коэффициенты используются для определения значимых факторов для модели. Они получены с достоверностью более 93%.

Из семи факторов три являются независимыми и соответствуют технологическим условиям обработки – эти три фактора учитывают взаимодействие технологических условий обработки. Один из независимых факторов (Ф2) в результате оценки значимости с вероятностью не менее 93,4% (рис. 2) признан статистически не значимым, соответственно, коэффициент регрессии a2 = 0.

Влияние фактора Ф2 (скорость линейной подачи S) для условий чистовой обработки можно рассматривать как случайное. Объяснить подобное явление можно тем, что при чистовом точении глубина резания сравнима по величине с радиусом при вершине резца и удельное влияние пластического деформирования в зоне обработки сравнимо с влиянием собственно процесса стружкообразования. Фактически имеет место явно выраженное обкатывание обрабатываемой поверхности [8].

Построенная степенная модель (рис. 4) достоверна с вероятностью более 90%. Качественное сравнение коэффициентов регрессии переменных позволяет выделить два значимых технологических фактора: скорость резания V и глубина резания t. Глубина резания имеет гораздо большее влияние (a3 = –0,502, рис. 3), чем скорость резания (a1 = –0,118, рис. 3), что также объясняется явно выраженным процессом поверхностного пластического деформирования и развитым силовым механизмом формирования свойств обработанной поверхности.

Черная линия с «отсечками погрешности» – экспериментальные данные, на основе которых построены модели. На рис. 2 показаны коэффициенты регрессии нормированных моделей – определенные без проверки статистической значимости (строка 14) и статистически значимые (строка 12). Выделенное поле – ячейки K6:N7 – представляет «виртуальный калькулятор» для вычисления высоты микронеровностей, прогнозируемой при определенных условиях обработки.

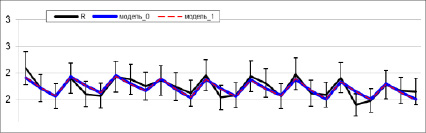
Рис. 4. Представление шероховатости поверхности для степенной модели

Заключение

С помощью статистического анализа выявлены два основных технологических фактора, определяющих формирование микропрофиля при чистовом точении углеродистой стали: скорость резания V и глубина резания t. Глубина резания оказывает значительное влияние на процесс резания. Поскольку глубина резания сопоставима с радиусом кривизны режущего инструмента, то при малых подачах и малых глубинах фактически не происходит резания. Вместо этого наблюдаются такие явления, как пластическое деформирование и трение. При увеличении глубины резания и скорости подачи (ширины и толщины срезаемого слоя) удельная доля процесса резания в совокупности механизмов формирования поверхностного слоя возрастает, влияние геометрии инструмента и температурных явлений на микропрофиль также увеличивается.

Вероятность корреляции между скоростью и шероховатостью составляет более 90%. Другими словами, чем выше скорость, тем ниже шероховатость. Глубина резания оказывает значительное влияние на шероховатость. При постоянной глубине резания шероховатость уменьшается, а коэффициент корреляции между этими двумя параметрами составляет 90%. Более глубокий срез может способствовать получению более чистой поверхности. Погрешность модели в среднем составляет 17%, что считается вполне приемлемым при прогнозировании сложных стохастических процессов. Вероятность того, что зависимость определена правильно, – более 90%.