Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Введение

Значение интенсивности входного потока является важной характеристикой любой системы массового обслуживания (СМО). Оно определяет количество требований (заявок), поступающих в систему за единицу времени, таким способом позволяя варьировать нагрузку.

При проектировании и моделировании систем массового обслуживания часто предполагается, что входной поток является стационарным. Это означает, что его интенсивность остается постоянной и не зависит от времени: λ = сonst.

Системы такого типа встречаются достаточно часто. Например, на производственных линиях поток изделий в течение дня может рассматриваться как стационарный. Однако было бы ошибкой рассматривать данный поток стационарным на более длинном промежутке времени. Это связано с тем, что объем производства зависит от спроса на продукцию, графика работы персонала и других факторов, прямо или косвенно влияющих на характер входного потока. Таким образом, этот и многие другие процессы обладают свойством стационарности только на достаточно ограниченном промежутке времени.

В отличие от классических СМО с постоянным входным потоком, в системах с нестационарным (переменным) потоком интенсивность поступления требований меняется с течением времени: λ = λ(t) [1, с. 17]. Интенсивность в системах такого типа может быть в линейной, экспоненциальной, синусоидальной и других зависимостях от времени. СМО с нестационарными потоками рассматриваются, например, в работах [2, 3]. Обзор существующих моделей нестационарных систем и методов их расчета приведен в работе авторов [4].

Модели систем, учитывающие свойство нестационарности, часто являются более реалистичными для решения современных задач с динамическим изменением параметров. Модели систем такого типа используются при анализе трафика, проектировании производственных и логистических систем, а также в других областях, требующих учета изменения частоты событий во времени. Изменение интенсивности может происходить в зависимости от времени суток, дня недели, сезона и других факторов.

Например, при исследовании потоков пассажиров общественного транспорта следует принимать во внимание, что трафик меняется в течение суток (утром и вечером пассажиров больше, чем днем), количество заказов в службах доставок также зависит от времени (количество заказов возрастает перед праздниками). Моделирование потоков в медицинских учреждениях (количество обращений зависит от сезона и времени суток) и розничных магазинах (количество покупок зависит от времени суток и дня недели), железнодорожных вокзалах и аэропортах (количество пассажиров зависит от расписания транспорта), телекоммуникационных сетях (повышенный трафик связан с деловой активностью), производственных процессах (количество изготавливаемой продукции зависит от спроса), операции на фондовом рынке (объем торгов зависит от экономической ситуации, новостей) – немногие примеры систем, в которых СМО с нестационарным входным потоком имеют прикладное значение.

Кроме нестационарного входного потока, многие реальные системы часто характеризуются неодинаковой скоростью работы приборов (каналов, обслуживающих устройств) [5–7]. Таким системам посвящено немало современных работ, например [8]. Особенностью систем такого типа является необходимость распределения потока заявок между свободными каналами [9–11]. При некоторых значениях нагрузки системы такого типа могут быть эффективнее классических систем с приборами одинаковой производительности [12].

Настоящая работа посвящена исследованию систем массового обслуживания, обладающих обоими свойствами – нестационарным входным потоком и приборами различной производительности. Несмотря на прикладную значимость моделей такого типа, в настоящее время они практически не изучены. Особый интерес представляют вопросы влияния нестационарного характера входного потока на эффективность систем с приборами различной производительности в сравнении с системами, обладающими приборами одинаковой производительности.

Объектом исследования являются модели СМО, функционирующие в условиях нестационарного входного потока. Целью работы является исследование влияния неоднородности приборов на функциональные характеристики системы массового обслуживания с нестационарным входным потоком.

Материалы и методы исследования

Математическое моделирование систем массового обслуживания, функционирующих в режиме нестационарных потоков, затруднено ввиду отсутствия общего решения в явном виде соответствующих им дифференциальных уравнений. С учетом этого для решения задач исследования применяются методы имитационного моделирования.

Для разработки моделей используется программный комплекс AnyLogic [13–15]. Данная среда предоставляет довольно широкий комплекс встроенных функций, обладает современным графическим интерфейсом и позволяет использовать язык программирования Java. На рисунке 1 представлена модель 2-канальной системы, состоящая из стандартных объектов среды AnyLogic.

Рассмотрим простейший пример системы с переменным потоком: СМО, интенсивность входного потока в которой задается кусочной функцией и является постоянной на некоторых промежутках времени. Расписание значений интенсивности входного потока системы представлено на рисунке 2.

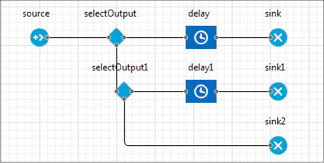
Рис. 1. Модель 2-канальной СМО Источник: составлено автором

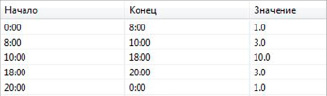
Рис. 2. Расписание значений интенсивности входного потока Источник: составлено автором

Таким образом, в рассматриваемой системе интенсивность входного потока меняется в течение дня от λ = 1 до λ = 10. Приближенно примером СМО такого типа может быть call-центр – служба поддержки некоторой организации. С указанной моделью проведен ряд вычислительных экспериментов, целью которых является сравнительный анализ эффективности СМО с приборами одинаковой и различной производительности. В ходе вычислительных экспериментов для исследования влияния нагрузки на показатели эффективности суммарная производительность системы варьировалась от μ1 + μ2 = 1 до μ1 + μ2 = 100.

Для исследования производительности рассматриваемых систем в качестве критериев эффективности используются вероятности состояний p0 и pотк в стационарном режиме. Здесь и далее полагаем, что p01 и p02 – вероятности отсутствия заявок в системе с приборами одинаковой и различной производительности соответственно, pотк1 и pотк2 – вероятности отказа в обслуживании соответственно для системы с приборами одинаковой и различной производительности.

СМО-1 – система с приборами одинаковой производительности, СМО-2 – система с приборами различной производительности. Для распределения заявок между приборами в СМО-2 используется алгоритм направления поступающих заявок на свободный прибор наибольшей производительности как наиболее эффективный для систем без функции накопления очереди [12].

Результаты исследования и их обсуждение

Рассмотрим результаты вычислительных экспериментов с имитационной моделью при крайне высокой нагрузке на систему. В таблице 1 представлены результаты расчетов для суммарной производительности приборов μ1 + μ2 = 1.

В столбцах «p02 – p01» и «pотк1 – pотк2» представлены области эффективности систем с разнотипными приборами, а именно разница между соответствующими значениями вероятностей стационарных состояний p02 – p01 и pотк1 – pотк2 для систем с приборами одинаковой (p01, pотк1) и различной (p02, pотк2) производительности. Таким образом, положительные значения ячеек указывают на то, что СМО с приборами различной производительности при соответствующих параметрах эффективнее классической СМО.

Таблица 1

Результаты вычислительных экспериментов с имитационной моделью СМО при μ1 + μ2 = 1

Примечание: составлено автором.

Таблица 2

Результаты вычислительных экспериментов с имитационной моделью СМО при μ1 + μ2 = 5

Примечание: составлено автором.

Таблица 3

Результаты вычислительных экспериментов с имитационной моделью СМО при μ1 + μ2 = 10

Примечание: составлено автором.

Очевидно, что рассматриваемой в таблице 1 суммарной производительности явно недостаточно для эффективной работы системы, о чем свидетельствуют большие значения вероятностей отказа. Данные таблицы 1 демонстрируют, что при небольшом различии в значениях производительности устройств (см. результаты при μ1 = 0,4 и μ2 = 0,6) показатели эффективности системы СМО-2 достаточно близки к показателям СМО-1.

При увеличении разницы в производительности устройств (см. результаты при μ1 = 0,2 и μ2 = 0,8) система массового обслуживания с неоднородными приборами оказывается менее эффективной по сравнению с классической системой, где все приборы обладают одинаковой производительностью.

В таблице 2 демонстрируются результаты имитационного моделирования при суммарной производительности приборов μ1 + μ2 = 5.

Снижение нагрузки на систему привело к увеличению разницы между значениями вероятностей состояний в стационарном режиме p02 – p01 и pотк1 – pотк2.

В таблице 3 представлены результаты вычислительных экспериментов при суммарной производительности μ1 + μ2 = 10. В данном случае общая интенсивность обслуживания совпадает с максимальной интенсивностью входного потока (см. расписание интенсивностей на рисунке 2).

Повышение суммарной производительности приборов также привело к увеличению разницы между значениями p02 – p01 и pотк1 – pотк2. Это позволяет утверждать, что при снижении нагрузки на систему СМО с приборами различной производительности становится эффективнее классической системы с однородными приборами

Таблица 4

Результаты вычислительных экспериментов с имитационной моделью СМО при μ1 + μ2 = 50

Примечание: составлено автором.

Вместе с тем, СМО-2 демонстрирует значительное снижение показателей эффективности при увеличении разрыва в производительности приборов.

К примеру, при μ1 = 1 и μ2 = 9 разница в показателях эффективности составляет p02 – p01 = – 0,072.

Рассмотрим данные, полученные с помощью имитационной модели при крайне низкой нагрузке на систему. Очевидно, что при суммарной интенсивности μ1 + μ2 = 50 система будет достаточно хорошо справляться с рассматриваемыми значениями входного потока.

Материалы таблицы 4 демонстрируют, что при незначительной нагрузке на систему (иными словами, если суммарная интенсивность приборов системы значительно больше интенсивности входного потока) система массового обслуживания с каналами различной производительности может быть более эффективна, чем классическая система с однотипными приборами (см. результаты таблицы 4). Увеличение диспропорции между производительностями обслуживающих устройств до определенного значения приводит к увеличению сравнительной эффективности СМО с приборами различной производительности, далее – к снижению.

Выводы

1. Разработана имитационная модель системы массового обслуживания, функционирующей в режиме нестационарных потоков. С помощью разработанной модели проведен ряд вычислительных экспериментов, в ходе которых исследовались области эффективности систем с приборами различной производительности.

2. Установлено, что при переменном входном потоке неоднородность приборов может обеспечивать более высокие эксплуатационные характеристики системы массового обслуживания. Таким образом, оптимальное сочетание интенсивностей входного потока и обслуживания позволяет увеличить пропускную способность СМО. Одновременно с этим чрезмерная диспропорция в производительности приборов значительно снижает общую эффективность системы.

3. Перспективы исследования темы включают в себя изучение механизмов эффективной работы с очередями, так как во время пиковых нагрузок нестационарные потоки могут приводить к образованию достаточно больших очередей; кроме того, достаточно перспективным представляется исследование моделей систем, позволяющих динамически менять интенсивность отдельных приборов в зависимости от текущей нагрузки.