Введение
В работе рассматривается возможность параллельного решения полной проблемы собственных значений с формулами собственных векторов матрицы. Подход опирается на метод Леверье с видоизменением Д.К. Фаддеева. Параллельные алгоритмы представляются на модели неветвящихся параллельных программ, понимаемой как последовательность шагов, на каждом из которых синхронно выполняются арифметические операции над готовыми значениями данных. Временная сложность алгоритма («время выполнения») обозначается Т(R) и измеряется числом последовательных операций, указывается их вид, а также количество требуемых процессорных элементов R (условно – процессоров). Время и способы обмена при этом не учитываются. Известные проблемы синтеза и анализа параллельных алгоритмов излагаются в [1, с. 443; 2]. Аспекты программирования параллельных алгоритмов обсуждаются, в частности, в [3, c. 43, 183]. Особенности адаптации к архитектурам параллельных вычислительных систем детально анализируются в [3, с. 69, 96, 136; 4]. Разновидности архитектуры суперкомпьютеров и их связь с классами решаемых задач описываются в [1, с. 94; 3, c. 43]. Общие тенденции развития параллельных вычислений отмечаются в [5].
Решение полной проблемы собственных значений включает нахождение всех собственных чисел матрицы. В рамках метода Леверье решение этой проблемы принято понимать как определение всех коэффициентов характеристического полинома. В целом решение проблемы подразумевает как вычисление корней характеристического полинома, так и поиск всех собственных векторов. Проблема актуальна для многих разделов математики, механики, техники и технологии. В небесной механике решение полной проблемы собственных значений связано с оценкой возмущения вековых орбит небесных тел [6, с. 295]. Именно с этой целью Леверье создал метод, который применял для анализа отклонений от расчетных орбит планет Солнечной системы [7, с. 15]. На основе оценок возмущения орбиты Урана был открыт Нептун. Обзор работ Леверье на эту тему с доступом к их электронным копиям представлен в [8, с. 518]. В приложении к оценкам возмущений метод применяется к матрице постоянных коэффициентов после линеаризации систем дифференциальных уравнений, описывающих движение небесных тел [9, с. 286]. Видоизменения классического метода используются в современных исследованиях в области планетной астрономии и движения космических тел [10].
Решение проблемы собственных значений принципиально для задач теоретической и прикладной механики. В квантовой механике при описании стационарных квантовых состояний решение уравнения Шредингера сводится к нахождению собственных функций и собственных значений гамильтониана:
Hψ = Eψ,
где E – нижний уровень энергии, ψ – волновая функция, H – гамильтониан [11].
Приложение задач на собственные значения к расчету вибраций в механических структурах описано, в частности, в [12, с. 202]. Применение решения полной проблемы собственных значений в теории пластичности материалов показано в [13, с. 42].
Среди разнообразных математических приложений полной проблемы собственных значений можно отметить непосредственное использование в теории и практике решения систем линейных дифференциальных уравнений с постоянными коэффициентами. На этой основе строится фундаментальная система решений. По виду и структуре собственных чисел матрицы коэффициентов формулируется критерий устойчивости линейной дифференциальной системы с важными применениями. В аналитической и дифференциальной геометрии с помощью решения полной проблемы собственных значений определяется канонический вид кривых и поверхностей. В алгебре на данной основе выполняется построение канонической формы Жордана для представления линейных операторов.
Значение полной проблемы собственных значений общеизвестно и отмеченными применениями не исчерпывается. Необходимо, однако, принять во внимание, что ее практическое решение связано с большим объемом вычислений, с проблемой вычислительной устойчивости, со значительным накоплением вычислительной погрешности [14, с. 110, 243, 384]. В известной мере это относится к методу Леверье, характеризующемуся объемом вычислений порядка O(n4). Поэтому в вычислительных приложениях предпочтением пользуются другие методы. В частности, используется метод вращений Якоби [14, с. 426]. Наиболее часто указывается на применение устойчивых разновидностей QR-алгоритма [15; 16]. Тем же отличается и [14, с. 426], где метод Леверье рассматривается в критическом аспекте [14, с. 384]. Метод Леверье подробно представлен преимущественно в учебных изданиях, например в [17, c. 311]. Тем не менее выбор этого метода в качестве предмета исследования обусловлен хорошо известными объективными отличиями. Во-первых, это единственный универсальный метод решения полной проблемы собственных значений, который не требует ограничений на вид матрицы. Во-вторых, это прямой (точный), а не итерационный метод, который за конечное число шагов дает решение. Аналогичным качеством обладает видоизменение Д.К. Фаддеева этого метода. В-третьих, в отличие от аналогов этот метод универсально дает дополнительные объекты алгебры, включая обратную матрицу (на основе соотношения Гамильтона – Кели), и тем самым решение системы линейных алгебраических уравнений. В-четвертых, что ценно для реализации на параллельных вычислительных системах, метод Леверье обладает максимально параллельной формой, позволяя на основе схемы Ксанки параллельно решить систему линейных алгебраических уравнений за конечное число шагов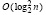 
[18].
До настоящего времени результат Ксанки не распространен на нахождение собственных векторов матрицы. В излагаемой ниже работе ставится задача построить параллельное решение полной проблемы собственных значений на основе метода Леверье с видоизменением Д.К. Фаддеева, которое включает параллельное вычисление матрицы собственных векторов. С этой целью указываются формулы представления собственных векторов в явном виде. Требуется по возможности уменьшить объем вычислений, снизить оценку временной сложности за счет максимально параллельной формы, при этом ограничить накопление вычислительной погрешности.
Цель исследования. Первая цель – выполнить преобразование метода Леверье решения полной проблемы собственных значений с видоизменением Д.К. Фаддеева, при котором достигается максимально параллельная форма преобразуемого метода с сохранением временной сложности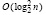 
для определения коэффициентов характеристического полинома и одновременно всех собственных векторов матрицы. Вторая цель – показать, что корни характеристического полинома можно найти также по параллельной схеме, сохранив по величине порядка указанную временную оценку.
Материалы и методы исследования
Исследование опирается на методы синтеза и анализа параллельных алгоритмов в приложении к вычислительной линейной алгебре.
Результаты исследования и их обсуждение
Предложено преобразование метода Леверье с видоизменением Д.К. Фаддеева, которое позволяет параллельно выполнять численное решение полной проблемы собственных значений. Преобразование отличается тем, что исключает последовательность шагов вычисления вспомогательных величин, представляя матрицу собственных векторов как матричный полином с числовыми коэффициентами. Отсюда формируется параллельное решение полной проблемы собственных значений с применением известной схемы Ксанки параллельного вычисления коэффициентов характеристического полинома и решения системы линейных алгебраических уравнений. От итерационных методов решения рассматриваемой проблемы предложенная разновидность отличается универсальностью, изначально присущей методу Леверье. Предложенное преобразование реализует прямой метод решения проблемы за конечное число шагов. В целом метод допускает максимальное распараллеливание с временной сложностью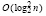 
для всей совокупности искомых объектов полной проблемы собственных значений. Попутно конструктивно вычисляется преобразование подобия и определяется структура матриц собственных векторов. Параллельное вычисление необходимо для сокращения времени численного моделирования многих процессов механики, опирающихся на решение полной проблемы собственных значений.
Исходные соотношения для решения полной проблемы собственных значений на основе метода Леверье.
Рассматривается однородная система линейных алгебраических уравнений (вековое уравнение)
Ax = λx, (1)
где A = (aij) – квадратная матрица, n×n, x – искомый собственный вектор. Требуется указать все значения λ, при которых решения (1) являются нетривиальными, требуется, иными словами, найти все собственные числа матрицы A. Условием для их определения является равенство нулю определителя системы (1):
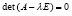, (2)
где E – единичная матрица. Уравнение (2) – характеристическое уравнение матрицы A. Развертывание (2) влечет полиномиальное уравнение с неопределенными коэффициентами.
Согласно [6, с. 295] ниже характеристическое уравнение записывается в виде
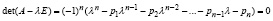. (3)
В скобках правой части (3) – характеристический полином матрицы A –
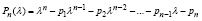. (4)
Относительно разновидности уравнения (3),
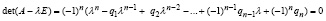, (5)
известно, что qi равно сумме всех диагональных миноров i-го порядка матрицы A [19, c. 403].
В частности,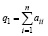 
, 
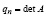. Из (3), (5) следует, что 
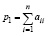и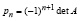 
. Ниже след матрицы A понимается как сумма ее диагональных элементов и обозначается 
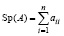. Элементы матрицы Aℓ обозначаются 
, 
.
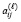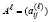Известно, что если λk – собственное число матрицы A, то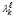 
есть собственное число матрицы Aℓ [6, с. 21]. При этом сумма диагональных элементов матрицы Aℓ есть
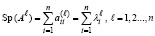[6, с. 295].
Пусть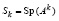 
. Корни полинома связаны с его коэффициентами уравнениями Ньютона, которые применительно к характеристическому полиному (4) примут вид [6, с. 295]
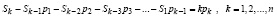, (6)
где подразумевается, что в левой части только не повторяющиеся слагаемые. Метод Леверье рекуррентно определяет из (6) коэффициенты pk , k = 1,2,…,n, поэтому включает априорное нахождение всех степеней матрицы до n-й включительно и их следов
, 
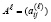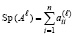, ℓ = 1,2,…,n. (7)
Уравнения (6) разворачиваются в виде [19, с. 417]
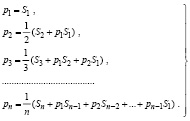(8)
Из (8) рекуррентно находятся искомые коэффициенты характеристического полинома.
С другой стороны, система (8) эквивалентна системе линейных алгебраических уравнений в приведенной форме относительно n неизвестных с нижней треугольной матрицей с нулевой диагональю. Именно,
P = SP + s,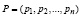 
, 
, 
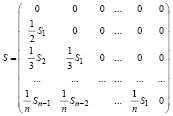. (9)
Решение системы (8) можно представить в виде
P = (E – S)–1s. (10)
Для обращения матрицы вида E – S известно несколько алгоритмов эффективного распараллеливания с оценкой временной сложности [18]
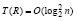, (11)
где число процессоров R = O(n3). Для характеристического полинома (4) имеет место тождество Гамильтона – Кели
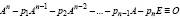. (12)
Здесь и ниже O – обозначение нулевой матрицы, что по контексту различается с обозначением порядка роста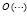 
. Из (12), в предположении pn ≠ 0,
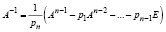. (13)
Ввиду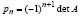 
предположение всегда выполнено для невырожденной матрицы A, и в этом предположении (13) дает решение системы линейных алгебраических уравнений. По алгоритму Ксанки все степени матриц находятся за логарифмическое число шагов [18]:
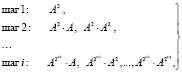(14)
где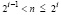 
. Отсюда 
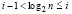. В точности 
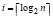. В максимально параллельной форме шаг i имеет временную сложность 
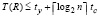, где ty и tc соответственно время бинарного умножения и сложения чисел, количество процессоров R ≤ n4. На основе параллельных разновидностей алгоритма Штрассена [20, с. 7] число процессоров в (14) может быть снижено. В дальнейшем эти разновидности не учитываются. Совокупность всех шагов (14) выполняется с временной сложностью
~ 
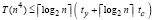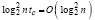. (15)
С учетом (10), (11) порядок оценки (15) сохраняется для всей схемы параллельного решения системы Ax = b с невырожденной матрицей A (после предварительного развертывания коэффициентов характеристического полинома из (14) [18]).
Ниже требуется показать, что с сохранением оценки (15) может быть не только параллельно решена рассматриваемая система, найдены все коэффициенты характеристического полинома, но и одновременно с тем могут быть параллельно найдены все собственные векторы векового уравнения (1).
Преобразование к параллельной форме видоизменения Д.К. Фаддеева метода Леверье. Известное видоизменение имеет вид [6, с. 296]:
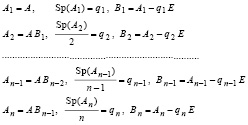
В [6, с. 297] доказано, что
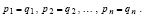(16)
Кроме того, Bn = O, и если det A ≠ 0, то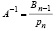 
.
Пусть из (14) уже найдены все степени матрицы, их следы (7), и пусть из (8), с переходом к (10), найдены все коэффициенты характеристического полинома. Тогда с учетом (16) видоизменение Д.К. Фаддеева можно переписать в виде
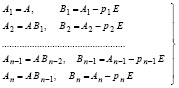. (17)
В силу индукции из (17) следует, что
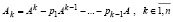, (18)
(соотношение (18) именно в таком виде используется в [6, с. 298]), и, кроме того,
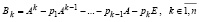. (19)
С помощью (19) в [6, с. 298] обосновывается следующая формула вычисления матрицы собственных векторов. Пусть все собственные числа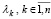 
, уже найдены и при этом оказались различными. Рассматривается матрица вида
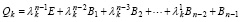. (20)
В [6, с. 299] показано, что каждый столбец матрицы Qk состоит из компонентов собственного вектора матрицы A, принадлежащего собственному числу λk, при этом Qk ≠ 0. С учетом (19) и (20) матрицу Qk можно в явной форме выразить через сумму последовательных степеней матрицы A, взятых с числовыми коэффициентами. Именно, искомое выражение находится с помощью подстановок Bk из (19) в формулу (20):
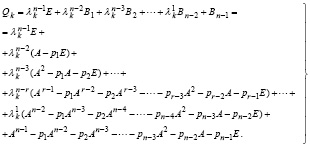(21)
Суммирование коэффициентов при одинаковых степенях матрицы Aℓ, ℓ = 0,1,…,n влечет
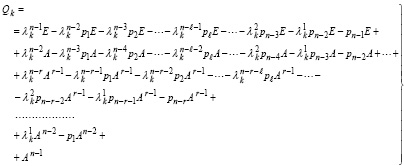(22)
или
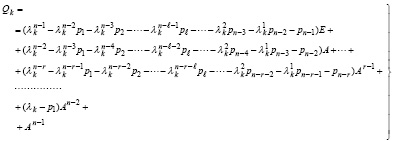(23)
Отсюда
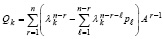. (24)
В краткой записи
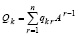, (25)
где
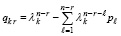. (26)
Обоснование того, что матрица (25) с коэффициентами (26) является матрицей собственных векторов матрицы A, соответствующих собственному числу λk, следует из сопоставления (20) с (24). Подробнее такое сопоставление будет развернуто в дальнейшем.
В (24)–(26) каждый коэффициент pℓ является коэффициентом из (8) с таким же индексом и совпадает с коэффициентом Pn(λ) из (4) с индексом численно равным ℓ, то есть с коэффициентом характеристического полинома при степени λn–ℓ. Коэффициенты (26) образуют убывающую по степеням с показателем n – r последовательность полиномов, взятых при значении λ = λk.
Последовательность начинается сразу после значения характеристического полинома
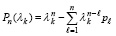, (27)
но собственно полином (27) в эту последовательность не входит, он абстрактно соответствует (26) при r = 0. Вид полиномов (26) аналогичен по структуре (27) в смысле соответствия убывающих показателей степени λ и возрастающих индексов коэффициентов.
В результате матрица собственных векторов Qk матрицы A в явной форме выражена через линейную комбинацию последовательных степеней матрицы Aℓ, ℓ = 0,1,…,n–1, в виде матричного полинома с числовыми коэффициентами из (24), что эквивалентно (25), (26). При использовании данного представления матрицы Qk нет необходимости предварительно вычислять матрицы Bk ,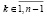 
, из (17), так как все степени для (25), (26) уже априори найдены при вычислении (7), в частности, по схеме (14). Априори также найдены все коэффициенты характеристического полинома (4), используемые в (24)–(26). Они вычислены из (8) или, что эквивалентно, из (9), (10). Собственные числа λk, 
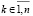, также предполагаются априори найденными и различными.
В итоге матрица Qk представлена явной формулой, позволяющей вычислить ее параллельно, исключая последовательные шаги (17).
Оценки временной сложности параллельного вычисления матриц собственных векторов. Пусть параллельно вычислены все Aℓ, ℓ = 0,1,…,n, по схеме (14) с оценкой (15), обратная матрица (13), а также все коэффициенты характеристического полинома Pn(λ) с оценкой (11). Пусть, кроме того, некоторым способом найдены все корни полинома Pn(λ) (требуемый способ обсуждается в дальнейшем вместе с оценкой временной сложности), и все они оказались различными. В этих предположениях для нахождения матрицы Qk собственных векторов матрицы A оказываются известными все компоненты выражений (25), (26). Требующими вычисления оказываются коэффициенты qkr из (26). Для их определения понадобится вычислить все степени собственного числа λk: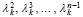 
. По схеме Стоуна это можно сделать параллельно на n процессорах (с помощью синхронного вычисления всех двоичных степеней и соединения из таких комбинаций степени с любым требуемым показателем) за время 
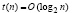. Если это сделать одновременно для всех априори найденных собственных чисел, то число процессоров возрастет в n раз:
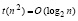. (28)
Дальнейшее вычисление qkr по формуле (26) потребует нахождения суммы парных произведений найденных таким образом степеней собственного числа на коэффициенты характеристического полинома, отдельно в сумму войдет слагаемое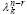 
. Для каждого фиксированного значения r из (26) с использованием схемы сдваивания это займет время
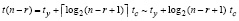. (29)
Для вычисления с сохранением оценки времени (29) одновременно всех qkr из (25) потребуется количество процессоров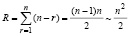 
. Так что оценку временной сложности вычисления всех искомых qkr можно записать в виде
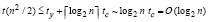. (30)
Если такое вычисление проделать одновременно для всех собственных чисел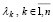 
, то количество процессоров возрастет в n раз, и оценка (30) перейдет в оценку
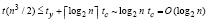. (31)
Локально, при вычислении значения полинома, число процессоров по сравнению с (28)–(31) можно сократить, если использовать следующую схему. Пусть рассматривается полином общего вида
.
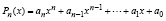Непосредственным умножением матриц слева направо оправдывается разложение
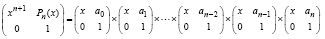. (32)
Значение полинома получается в верхней правой клетке левой части (32). Применение к правой части схемы сдваивания влечет следующую оценку параллельного вычисления значения полинома
,
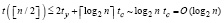где учитывается, что каждое умножение данных матриц сохраняет их структуру, так что две нижние клетки заполнять не нужно. Помимо экономии процессоров схема удобна тем, что позволяет перемножать матрицы слева направо и справа налево. Кроме того, она реализуема и последовательно. В отличие, в частности, от схемы Горнера схема (32) двунаправленна, то есть позволяет вести умножение от младших коэффициентов к старшим (слева направо) и от старших к младшим (справа налево), в таком варианте коэффициенты могут поступать динамически по ходу их вычисления без априорного хранения в памяти. При последовательном вычислении коэффициентов (26) схема (32) позволяет за n шагов получить сразу все коэффициенты формулы (25), поскольку каждый последующий коэффициент получается из предыдущего на каждом шаге умножения матриц справа налево (что очевидно из (23)).
Остается найти значение матричного полинома (25) с учетом того, что все степени матриц априори найдены. Одновременное их умножение на вычисленные коэффициенты qkr параллельно выполняется за время ty при количестве процессоров R ≤ n3. С половиной такого количества процессоров полученные после умножения на коэффициенты степени матриц можно сложить по схеме сдваивания с оценкой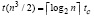 
. Объединение рассмотренных оценок влечет следующую оценку временной сложности вычисления матрицы собственных векторов Qk, представленную в (25), (26), –
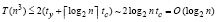. (33)
Если такие вычисления выполнить одновременно для всех матриц Qk,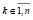 
, то число процессоров увеличится в n раз, оценка (33) перейдет в оценку 
.
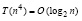Из изложенного вытекает
Теорема 1. Пусть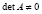 
и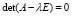 
. Пусть по методу Леверье с применением тождества Гамильтона – Кели и схемы Ксанки параллельно выполнено вычисление всех степеней матриц (14), параллельно решена треугольная система (9), (10), согласно которой получены все коэффициенты характеристического полинома (4) и параллельно найдена обратная матрица A–1 из (13) с суммарной оценкой временной сложности (15). Если, кроме того, найдены все собственные числа 
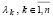, матрицы A и при этом все они оказались различными, то имеет место следующее утверждение. Все собственные векторы матрицы A, соответствующие отдельно взятому собственному числу λk , могут быть найдены из соотношений (25), (26) по описанной выше параллельной схеме с временной сложностью 
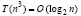. Одновременно все собственные векторы, соответствующие всем собственным числам 
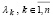, матрицы A, могут быть найдены параллельно из соотношений (25), (26), примененных ко всем k = 1,2,…,n, с временной сложностью 
.
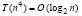Следствие 1. В условиях теоремы 1 все вычисления по схеме Ксанки и вычисление матриц всех собственных векторов в совокупности выполняются параллельно с временной сложностью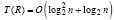 
, или, 
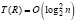, где R = n4.
Замечание 1. Исключение согласно условию теоремы составляют операции нахождения корней характеристического полинома, которые обсуждаются непосредственно ниже. С точностью до этой принципиальной оговорки операции по параллельному вычислению собственных векторов по величине порядка сохраняют оценку временной сложности (15) известной схемы Ксанки. Ниже оценивается возможность сохранить порядок оценки (15) с учетом временной сложности нахождения всех корней характеристического полинома, то есть всех собственных чисел матрицы A.
Оценка временной сложности параллельного вычисления всех собственных чисел матрицы A. В [21, с. 268] изложен метод вычисления всех корней характеристического полинома матрицы с учетом кратности, основанный на применении устойчивой адресной сортировки, которая допускает максимально параллельную форму. В этой работе приводится программа [21, с. 269] и описывается схема ее максимального распараллеливания. Формально такая схема позволяет все корни характеристического полинома найти с оценкой временной сложности следующего вида [21, с. 275]:
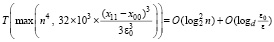, (34)
где в скобках левой части – число процессоров. В (34) n – порядок матрицы, ε – априори заданная граница абсолютной погрешности вычислений, ε0 – априори заданный радиус локализации каждого корня, x11 – x00 – длина стороны квадрата, ограничивающего область корней характеристического полинома, d > 1 – априори заданный постоянный числовой параметр. Согласно [6, с. 132, 133] все собственные числа матрицы A лежат в объединении кругов Гершгорина
, 
, 
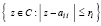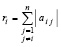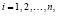(35)
где ri – сумма модулей внедиагональных элементов i-й строки матрицы. Из (35) для корней характеристического полинома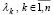
, верна оценка 
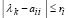. Отсюда 
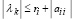. Подстановка ri из (35) влечет
.
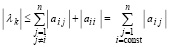С применением первой канонической нормы матрицы получится
, 
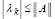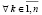, где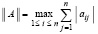 
[6, с. 133].
Рассматриваемая программа сама находит уточненные границы расположения корней [21, с. 259], если априори границы сверху указать в произвольно фиксированном приближении. В качестве стороны квадрата, ограничивающего область корней, можно взять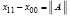 
. Подстановка в (34) влечет
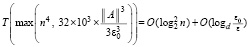. (36)
В (36) величины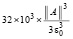 
, а также 
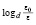– априори задаваемые постоянные числовые параметры. За исключением ||A|| эти параметры от n не зависят. Следовательно, оценку (36) можно переписать в виде 
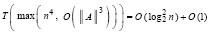, или
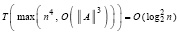. (37)
Очевидно,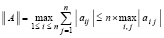 
.
Отсюда (37) переходит в оценку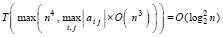 
.
Если элементы матрицы считать априори равномерно ограниченными,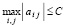 
, где C = const, то 
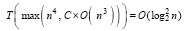, следовательно,
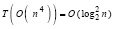, (38)
где число процессоров R = O(n4) практически весьма велико, но при этом имеет порядок роста n4, как в оценке Ксанки (15). Таким образом, имеет место
Предложение 1. Пусть матрица A, n×n, удовлетворяет условиям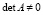 
и 
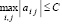, где C = const. Тогда все корни характеристического полинома этой матрицы могут быть параллельно вычислены с априори заданной границей абсолютной погрешности ε с временной сложностью (38). В условиях теоремы 1 оценка (38) сохраняется для одновременного вычисления всех собственных чисел и всех собственных векторов, соответствующих всем собственным числам матрицы A.
Некоторые следствия явного выражения собственных векторов через степени матрицы. Пусть выполнены все условия теоремы 1. Из того, что
AQk = λkQk, (39)
следует, что A2Qk = λkAQk. Отсюда и из (39)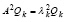 
. По индукции,
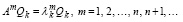(40)
Подстановка (25) влечет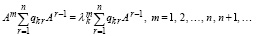 
, или,
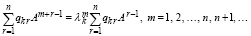(41)
С учетом (26)
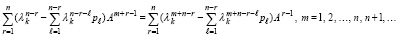(42)
Следствие 2. Для любой матрицы A и любого ее собственного числа λk в условиях теоремы 1 выполнены равенства (41), (42), где pℓ совпадают с коэффициентами характеристического полинома Pn(λ) из (4) при равных значениях индексов. Эквивалентной формой (42) является равенство
,
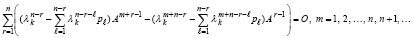которое означает, что в условиях теоремы 1 любая матрица A является корнем матричного полинома из левой части равенства при любом значении m.
В тех же условиях из (40), (25), (26) получается еще одно представление матрицы собственных векторов: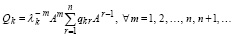 
, или,
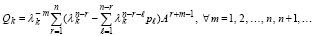
Далее, из (39) следует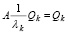 
и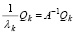 
, или,
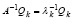. (43)
Из (43), по аналогии с (40),
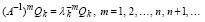(44)
Подстановка (25) влечет
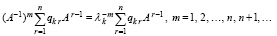(45)
С учетом (26)
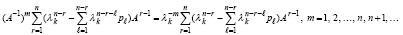(46)
Следствие 3. Для любой матрицы A и ее собственного числа λk, а также для обратной к ней матрицы A–1 и ее собственного числа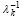 
в условиях теоремы 1 выполнены равенства (45), (46), где pℓ совпадают с коэффициентами характеристического полинома Pn(λ) из (4) при равных значениях индексов. Эквивалентной формой (46) является равенство
,
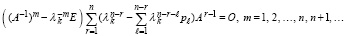означающее, что в условиях теоремы 1 любая матрица A является корнем матричной функции из левой части равенства при любом натуральном m. Кроме того, замена в левой части (44) Qk из (25), (26) влечет еще одно представление матрицы собственных векторов:
,
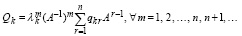или
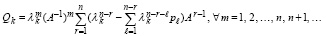
В другой форме связь матрицы собственных векторов с обратной матрицей вытекает непосредственно из (21). Последняя строка этого разложения совпадает с выражением в скобках (13), то есть с обратной матрицей, умноженной на pn. Поэтому разложение можно переписать в виде
,
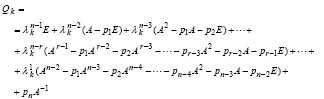или
.
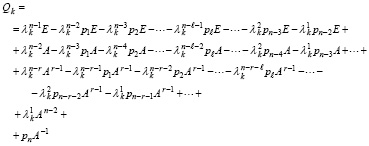Отсюда
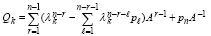, (47)
или
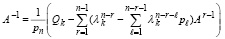. (48)
Следствие 4. В условиях теоремы 1 матрица собственных векторов Qk матрицы A и обратная матрица A–1 связаны соотношениями (47) и (48).
Можно указать дополнительные разложения матрицы собственных векторов Qk по степеням матрицы A. Именно, в (22) каждую строчку с фиксированной степенью матрицы можно преобразовать так, что коэффициент примет вид характеристического полинома. С учетом того, что значение характеристического полинома Pn(λ) из (4) берется при значении корня, Pn(λ) = Pn(λk) = 0, преобразование первой строчки (22) примет вид
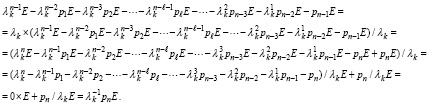
Аналогично, для второй строчки (22) получится
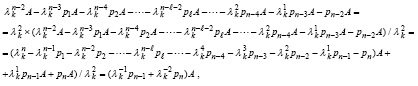
для r-й строчки –
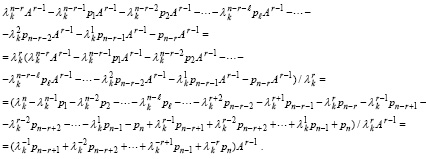
Здесь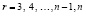 
.
В результате
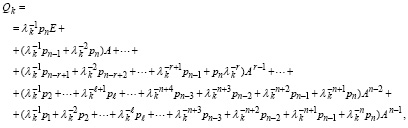
или
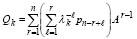. (49)
Из (24) и (49) следует равенство правых частей,
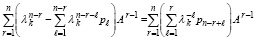, (50)
а по построению (49) получается равенство коэффициентов в правых частях:
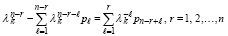. (51)
Следствие 5. В условиях теоремы 1 для любой матрицы A матрица Qk собственных векторов, соответствующих отдельно взятому собственному числу λk, представима в виде (49), матрица A удовлетворяет равенству (50), коэффициенты удовлетворяют уравнениям (51).
Как отмечалось, обоснование того, что матрица (25) с коэффициентами (26) является матрицей собственных векторов матрицы A, соответствующих собственному числу λk, следует из (16)–(23). Ниже прилагается структурное дополнение к обоснованию. Условие (39) эквивалентно условию
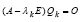. (52)
Подстановка в (52) Qk из (25) влечет
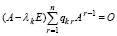, (53)
или
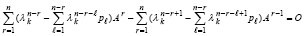. (54)
Для раскрытия связи выражений с парой соседних индексов в (54) рассматривается сумма двух соседних строк (22) –
.
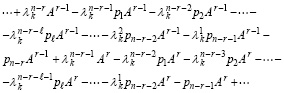Первая из этих двух строк совпадет со второй при умножении первой строки на A, а второй строки – на λk, если дополнительно вычесть из умноженной на λk второй строки выражение pn–rAr. Именно так связаны слагаемые с одноименными соседними индексами в (54). Выражение в скобках второго слагаемого, содержащего Ar–1, получается из слагаемого, содержащего Ar, умножением на λk, и при этом первое слагаемое априори уже включало умножение на A согласно (52), (53). Если первое слагаемое умножить на λk, а второе на A и вычесть из него pn–rAr, то оба слагаемых совпадут. Рассматриваемые операции в точности соответствуют индексу r первого слагаемого и индексу r+1 второго слагаемого для допустимых значений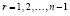 
. При этом они имеют противоположный знак. Таким образом,
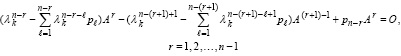(55)
Из (54) и (55) следует, что с вычитанием добавленных слагаемых, а также с учетом слагаемых, не вошедших при сдвиге по r начальных и конечных индексов, получится
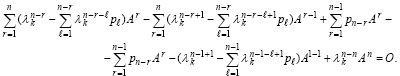
Если к левой части этого равенства добавить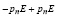 
, равенство преобразуется к виду
,
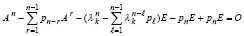или,
.
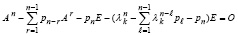Окончательно,
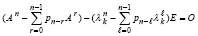. (56)
Равенство (56) оправдано по соотношению Гамильтона – Кели применительно к первой паре скобок и по определению характеристического полинома, взятого в корне этого полинома, применительно ко второй паре скобок.
В силу обратимости изложенных преобразований имеет место
Предложение 2. В условиях теоремы 1 подстановка в левую часть (52) Qk из (25) влечет преобразование левой части к виду
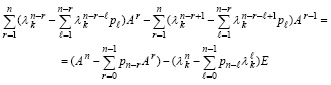. (57)
С учетом (56) это равенство эквивалентно равенству (54), которое означает, что любая матрица A в рассматриваемых условиях является корнем матричного полинома левой части (54). Каждое из равенств (57) и (54) показывает, что Qk из (25) удовлетворяет характеристическому уравнению (52), и, таким образом, Qk является матрицей, столбцы которой совпадают с собственными векторами матрицы A, соответственными ее характеристическому значению λk при любом фиксированном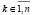 
.
Структура матриц собственных векторов в случае преобразования подобия. Преобразование подобия H–1AH, где H – невырожденная матрица, n×n, не меняет собственных значений матрицы A, а собственные векторы подобной матрицы H–1AH получаются из собственных векторов матрицы A их умножением на матрицу H–1 [14, с. 24]. Рассматриваемая матрица A невырожденная, все ее собственные значения различны, поэтому существует преобразование подобия, которое преобразует эту матрицу к канонической форме Жордана, такой, что на диагонали матрицы расположены собственные числа, остальные ее элементы – нули. Ниже диагональная форма матрицы, полученной в результате преобразования подобия матрицы A, обозначается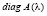 
. Если 
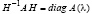, то на диагонали матрицы 
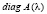расположены все собственные числа 
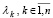, при этом матрица H состоит из n столбцов, каждый из которых совпадает с собственным вектором матрицы A, соответствующим одному и только одному из данных собственных чисел λk [14, с. 24]. Столбцы матрицы H линейно независимы [14, с. 22], поэтому 
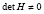и существует H–1. Таким образом, в рассматриваемом случае, когда все 
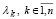, различны, преобразование подобия H–1AH заведомо существует. Ниже детализируются структуры матриц собственных векторов в случае выполнения этого преобразования. Пусть согласно (24)–(26) вычислены матрицы собственных векторов Qk, соответствующих каждому собственному числу 
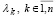. Из n матриц Qk можно выбрать по одному столбцу и составить из них столбцы матрицы H. Столбцы отвечают n различным собственным числам, так что 
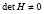, и сформированная матрица H удовлетворяет требованиям искомого преобразования (можно из каждой матрицы Qk выбирать по одному первому слева направо столбцу). Для преобразования подобия нужна, кроме того, обратная матрица H–1. Поскольку H уже сформирована, то H–1 можно найти по формуле (13), заменив в ней A на H, если только предварительно по схеме (8) найти соответственные этой матрице коэффициенты. С изменением обозначений коэффициентов получится
,
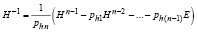где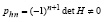 
. В результате окончательно сформируется 
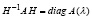. Для преобразованной матрицы в полной аналогии (24)–(26) получится
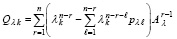, (58)
где для компактности записи обозначено
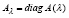. (59)
Для дальнейшего соответственная (59) матрица H преобразования подобия обозначается Hλ, так что
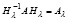. (60)
В силу диагональной структуры матрицы (59), (60)
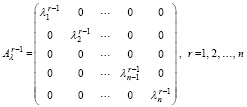. (61)
Из (61)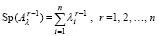 
. Поэтому 
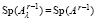, и поскольку в (6) 
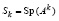, то решение уравнений (6) в виде (8) дает одинаковые значения коэффициентов 
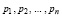характеристического полинома (4) матрицы A и характеристического полинома
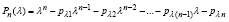
матрицы Aλ. Отсюда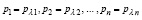 
, и соотношение (58) можно переписать в виде
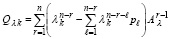. (62)
Согласно (62) для вычисления матрицы собственных векторов Qλk, соответствующих собственному числу λk матрицы (59), вычислять коэффициенты pλℓ заново не потребуется. Не требуется также заново вычислять степени матрицы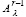 
, поскольку рассматриваемый поиск собственных векторов предполагает априори найденными все 
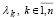. Степени диагональных элементов (61) также уже вычислены при нахождении коэффициентов (26). В рассматриваемом преобразовании подобия (60) матрица собственных векторов Qλk матрицы Aλ получается из матрицы собственных векторов Qk матрицы A путем умножения на 
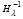, то есть
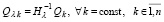, (63)
поэтому
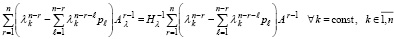, (64)
что эквивалентно
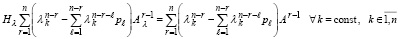. (65)
Матрицу собственных векторов (63) можно определить непосредственно. Именно, матрица умножается на число поэлементно и матрицы складываются поэлементно. Поэтому в левой части (64) все множители можно внести под знак степени матрицы,
,
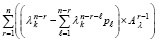и после суммирования полученных матриц, с учетом структуры матрицы (61), вся левая часть (64) преобразуется в одну матрицу вида
(66)
Матрица (66) является диагональной. Поскольку равные матрицы равны поэлементно, то правая часть (64) также является диагональной матрицей. Имеет место
Предложение 3. В условиях теоремы 1 для любой матрицы A выполняется равенство (64), где в левой части располагается матрица собственных векторов матрицы Aλ, полученной в результате преобразования подобия (60). При этом матрица собственных векторов левой части соответствует собственному числу λk матрицы A, которое равно собственному числу матрицы Aλ. Данная матрица имеет диагональную структуру и записывается в виде (66), где собственное число λk матрицы A присутствует с различными показателями степени в скобках выражений на диагонали. В правой части равенства (64) располагается матрица Qk собственных векторов матрицы A из (24), соответствующих тому же собственному числу λk, которая умножается на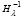 
из (60). Матрица правой части также становится диагональной, элементы ее диагонали совпадают с элементами диагонали (66). Данная структура рассматриваемых подобных матриц имеет место для каждого собственного числа λk ,
.
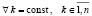Следствие 6. Все различные собственные векторы матрицы Aλ из (59), (60), соответственные собственному числу λk этой матрицы (или, что то же, матрицы A), совпадают со всеми различными столбцами матрицы (66) в порядке их расположения.
Следствие 7. В силу обратимости матрицы (66) с сохранением диагональной структуры матрица правой части (64) также обратима с сохранением диагональной структуры. В случае обращения обе части равенства будут определяться из (66) путем деления единицы на элемент диагонали в каждой строке:
.
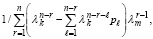
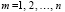Таким образом, в условиях теоремы 1 могут быть найдены не только все собственные векторы матрицы A, соответственные каждому собственному числу λk этой матрицы, но одновременно с тем могут быть определены все соответственные тому же собственному значению собственные векторы матрицы Aλ, являющейся результатом преобразования подобия (60). При этом собственные векторы соответствуют каждому собственному числу λk матрицы Aλ и вычисляются как столбцы матрицы Qλk по схеме (58), которая эквивалентна (62). Все вычислительные компоненты схемы (62) становятся известными на стадии вычисления собственных векторов матрицы A. Как отмечалось, все степени на диагонали в (61) уже вычислены на этапе определения коэффициентов (26) для матрицы Qk из (24). Тогда же найдены все значения коэффициентов в скобках (62). Остается только их умножить на диагональные элементы матриц (61), затем сложить по схеме сдваивания полученные матрицы. В результате дополнительное вычисление матрицы Qλk из (62) можно выполнить параллельно с логарифмической оценкой времени, что не изменит порядка оценки теоремы 1. Порядок оценки не изменится и по количеству процессоров, включая случай одновременного вычисления всех таких матриц Qλk для всех собственных чисел λk,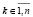 
.
Из изложенного вытекает
Теорема 2. В условиях теоремы 1 для любой матрицы A наряду с матрицей собственных векторов Qk из (24), соответствующих ее собственному числу λk, по схеме (62) можно параллельно вычислить матрицу собственных векторов Qλk, соответствующих тому же собственному числу λk матрицы Aλ, полученной в результате преобразования подобия (60). При этом порядок оценки временной сложности (38) не изменится ни по времени, ни по количеству процессоров, включая случай одновременного вычисления всех таких матриц Qλk для всех собственных чисел λk ,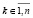 
.
Следствие 8. Утверждение теоремы 2 распространяется на одновременное параллельное вычисление матриц преобразования подобия Hλ,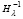 
. Кроме того, утверждение теоремы 2 сохраняется и конкретизируется при выполнении (63)–(65) и (66).
Следствие 9. Вычисления теоремы 2 можно выполнять непосредственно из (66) без изменения отмеченного порядка временной сложности.
Следствие 10. Согласно (65), (66) матрица Qk собственных векторов матрицы A, соответственных собственному числу λk этой матрицы, будет диагональной, если существует преобразование подобия (60), при котором матрица Hλ является диагональной, и именно в такой диагональной форме эта матрица использована в левой части (65).
Предложенное преобразование метода Леверье с видоизменением Д.К. Фаддеева позволяет параллельно выполнять численное решение полной проблемы собственных значений. При этом принимается стандартное ограничение исходного метода – предположение о том, что все собственные числа различны. Непосредственно от прототипа преобразование отличается тем, что исключает последовательность из n шагов (17) по вычислению вспомогательных величин и матриц, как результат представляет матрицу собственных векторов, соответствующую отдельно взятому собственному значению, в виде матричного полинома с числовыми коэффициентами. Параллельное решение полной проблемы собственных значений включает известную схему Ксанки, по которой параллельно находятся собственные числа и решение системы линейных алгебраических уравнений. К этой известной схеме добавляется предложенная схема параллельного вычисления собственных векторов. От других известных методов решения рассматриваемой проблемы предложенная разновидность отличается свойством универсальности, которым изначально обладает метод Леверье. Существенно, что метод Леверье, как и видоизменение Д.К. Фаддеева, представляет собой прямой (точный) метод, применение которого дает искомое решение за конечное число шагов вычислительного алгоритма. Дополнительно можно заметить, что известные аналоги, как правило, не предполагают априорного вычисления собственных значений, в то время как предложенное преобразование опирается на приближенное вычисление корней характеристического полинома с помощью устойчивой адресной сортировки. Вычисление корней выполняется с точностью до формата представления данных в языке программирования для полиномов высокой степени [22], при этом программа допускает максимальное распараллеливание, что позволяет сохранить оценку временной сложности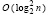 
для всей совокупности искомых объектов, включая вычисление собственных чисел и собственных векторов. Попутно с сохранением той же временной оценки в рамках предложенного подхода конструктивно вычисляется преобразование подобия. Кроме того, в рамках предложенного преобразования получается ряд структурных соотношений между матричными полиномами, представляющими собственные векторы, и конструктивно указывается связь между собственными векторами и обратной матрицей. Недостатком обсуждаемого метода является большой объем вычислений в случае последовательного выполнения, хотя возможна естественная рационализация предложенного алгоритма. Параллельное вычисление необходимо для сокращения времени численного моделирования многих процессов механики, опирающихся на решение полной проблемы собственных значений. Рассматриваемые преобразования и их результаты не относятся к случаю, когда среди собственных чисел матрицы имеются кратные. Работа включает явные формулы собственных векторов матрицы, а также их видоизменений в случае преобразования подобия. Это может оказаться целесообразным для оценок возмущений в приложениях к задачам механики.