Введение
В последние годы актуальность использования возобновляемых источников энергии стала очевидной и обсуждаемой в различных сферах общества. Одним из перспективных направлений является использование солнечной энергии. Однако в настоящее время многим системам, работающим на солнечной энергии, трудно конкурировать с традиционными энергетическими системами. В связи с этим большое количество работ направлено на улучшение солнечных тепловых коллекторов с целью повышения их производительности [1]. Одним из направлений улучшения показателей солнечных коллекторов является возможность применения наножидкостей (коллоидных суспензий) в качестве теплоносителя в системах подобного типа [2, 3].
Наножидкостные солнечные коллекторы прямого поглощения (НКПП) являются достаточно новым решением по получению возобновляемой энергии. Для их проектирования и разработки необходимо проведение исследований с применением математического моделирования для определения, при каких параметрах наножидкости, интенсивности светового поля, скорости течения теплоносителя, а также геометрических характеристиках НКПП будут наиболее производительными. Применение методов математического моделирования позволяет детально изучать теплофизические процессы в таких коллекторах, оптимизировать их параметры, существенно сокращать временные и материальные издержки на их создание. Такая работа имеет большое практическое значение, так как способствует созданию эффективных солнечных электростанций и снижению нагрузки на окружающую среду. В настоящее время научными коллективами активно проводятся исследования в данном направлении. Разрабатываются новые математические модели, учитывающие, например, процессы конвекции наножидкости при различных размерах коллектора, наклонах и объемных долях наночастиц, а также исследуются экспериментальные разработки солнечных коллекторов с наножидкостями [4, 5]. В работе Z. Said и соавт. выполнен обзор имеющихся моделей, акцент делается на термической, экономической и экологической оценке изучаемых систем, а также на обсуждении возможных ограничений использования наножидкостей [6]. Отдельный интерес представляет обзорная статья [7], в которой поставлен ряд исследовательских задач, остающихся актуальными до сегодняшнего дня.
Несмотря на большое количество исследований, о промышленном применении солнечных коллекторов на наножидкостях речь в настоящее время не идет. В связи с этим исследование и моделирование процессов в данном направлении является актуальной задачей. В данной работе авторы сосредоточились на вопросе определения величины интенсивности солнечного излучения внутри коллектора, исследовании зависимости интенсивности солнечного излучения от материалов базовой жидкости и диспергированных в ней частиц.
Цель исследования – на основе моделирования процессов внутри наножидкостного солнечного коллектора прямого поглощения выполнить расчет интенсивности солнечного излучения внутри коллектора, провести вычислительные эксперименты по установлению зависимости интенсивности солнечного излучения от материалов базовой жидкости и диспергированных в ней частиц.
Материалы и методы исследования
Моделирование интенсивности солнечного излучения внутри солнечного коллектора является важной задачей при проектировании и оптимизации солнечных энергетических систем. Далее в статье рассматривается плоский солнечный коллектор, состоящий из элемента, поглощающего солнечное излучение (абсорбер), прозрачного покрытия и термоизолирующего слоя [8]. Абсорбер связан с теплопроводящей системой и покрывается черной краской либо специальным селективным покрытием для повышения эффективности. Прозрачный элемент обычно изготавливается из закаленного стекла с пониженным содержанием металлов либо особого рифленого поликарбоната. Задняя часть панели покрыта теплоизоляционным материалом, который накапливает энергию с помощью гелиотермального способа. Внутри коллектора располагается базовая жидкость с наночастицами, причем предполагается, что наночастицы – это шарообразные частицы диаметром 1–100 нм, среднее расстояние между соседними твердыми частицами намного больше их диаметров, кинетическая энергия твердых частиц в жидкости пренебрежимо мала, объемная доля частиц в наножидкости не превышает 0,05.
Задача определения величины интенсивности солнечного излучения определенной длины волны сформулирована в виде задачи Коши для обыкновенного дифференциального уравнения первого порядка. Суммарное значение величины интенсивности излучения вычисляется интегрированием по всему спектру излучения.
Для проведения вычислительных экспериментов при исследовании создан программный комплекс на языке Python в IDE PyCharm Community Edition 2021.1.1 x64. Для решения задачи Коши использован метод Рунге – Кутты четвертого порядка, численное интегрирование выполнено методом Симпсона.
Результаты исследования и их обсуждение
Перейдем к математической постановке задачи [9]. Рассмотрена прямоугольная область, имитирующая солнечный коллектор с длиной и высотой L и H (рис. 1). Учитывая специфику работы устройства данного типа, обязательным условием является  .
.
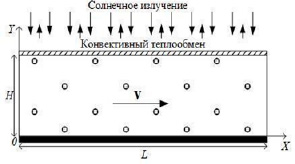
Рис. 1. Упрощенная схема солнечного коллектора Источник: составлено авторами на основе [8]
С целью описания процесса прохождения солнечного излучения через коллектор, в рамках которого происходит ослабление светового потока, необходимо решить задачу Коши относительно интенсивности солнечного излучения Iλ(y) [9, 10]:
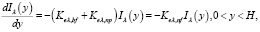 (1)
(1)
Iλ(H) = τIb,λ. (2)
Подробное описание математической постановки, а также используемых величин и коэффициентов приведено в работе [9].
Для наножидкостей, в которых присутствие мелких частиц влияет на характер поглощения, а также на характер рассеяния, необходимо использовать некоторые соотношения, такие как, например, приближение рэлеевского рассеяния [11].
Это приближение справедливо, когда  и
и  , где α и m – размер и комплексный показатель преломления наночастиц соответственно, и определяются по следующим формулам:
, где α и m – размер и комплексный показатель преломления наночастиц соответственно, и определяются по следующим формулам:
α = πdp / λ, m = (nnp + iκnp) / nbf, (3)
где dp – диаметр частиц; nnp и κnp – показатель преломления и коэффициент экстинкции материала наночастиц; nbf – показатель преломления базовой жидкости [12].
Значения для оптических величин nnp – показатель отражения, κnp и nbf – показатели поглощения материала наночастиц и базовых жидкостей заимствованы из базы данных MiePlot v4621 [13].
С физической точки зрения, используя рассеяние Рэлея, необходимо помнить, что размер используемых наночастиц должен быть намного меньше длины волны падающего излучения. Исходя из этого спектральный показатель ослабления необходимо определить по формуле
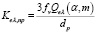 , (4)
, (4)
где fv – объемная доля частиц, Qeλ(α,m) – эффективность экстинкции в режиме Рэлея, которая определяется по следующей формуле
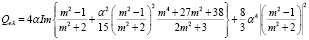 , (5)
, (5)
где член эффективности экстинкции (Qeλ) равен сумме эффективности поглощения (Qaλ) и эффективности рассеяния (Qsλ), которые соответственно вычисляются по формулам
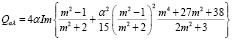 ,
, 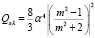 .
.
Подставляя выражения (3) и (5) в (4), получаем следующую формулу для вычисления Keλ,np [6]:
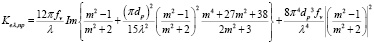 .
.
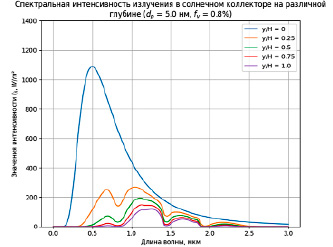
Рис. 2. Спектральная интенсивность излучения в солнечном коллекторе на различной глубине Источник: составлено авторами
Решение (1) можно получить в явном виде. Общее решение уравнения имеет вид
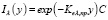 . (6)
. (6)
Далее найдем константу С, используя граничное условие (2). Имеем
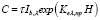 .
.
Подставляя значение константы С в (6), получаем искомое решение
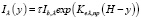 . (7)
. (7)
При помощи программного обеспечения, разработанного авторами [9], проведены вычисления, позволяющие исследовать зависимость интенсивности излучения от свойств наножидкости. Ранее авторами выполнено исследование по сравнению поглощающих свойств наножидкостей, состоящих из дистиллированной воды и этиленгликоля [14].
На рис. 2 представлены результаты моделирования спектральной интенсивности солнечного излучения, проходящего сквозь коллоидную суспензию, состоящую из наночастиц алюминия, а в качестве основы (базовой жидкости) была использована дистиллированная вода. При моделировании были использованы следующие начальные данные: высота коллектора H =1,2 мм, диаметр частиц dp = 5нм, объемная доля частиц fv = 0.8% [10]. Из рис. 2 видно, что в верхней части НКПП значение спектральной интенсивности достигает максимального значения и довольно быстро уменьшается по мере прохождения светового потока. Это происходит в связи с тем, что наножидкость обладает селективными свойствами, из-за которых происходит избирательное поглощение и рассеивание солнечного излучения в зависимости от длины волны. Наибольшее ослабление интенсивности происходит в области примерно от 0,5 до 1 мкм, где присутствует большая часть энергии падающего солнечного света. Как упоминалось ранее, в этих расчетах пренебрегалось атмосферным поглощением и различными составляющими газами, поэтому в спектральном распределении интенсивности не видны резкие перепады, которые могли бы появиться в противном случае.
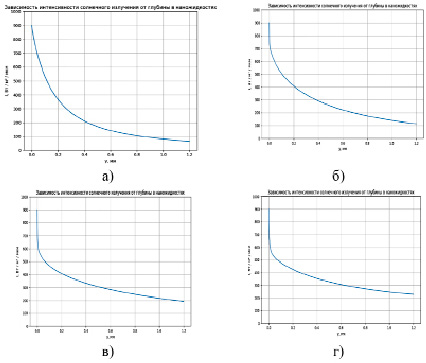
Рис. 3. Распространение интенсивности солнечного излучения для частиц различных металлов: а) алюминия; б) серебра; в) золота; г) меди Источник: составлено авторами
Выражение (7) описывает интенсивность солнечного излучения в наножидкости в зависимости от длины волны излучения и координаты y. Чтобы получить общую интенсивность излучения и ее производную в определенной точке коллектора, нужно проинтегрировать выражение (7) по всему диапазону длин волн солнечного излучения.
Интегрируя (7) на отрезке [λmin, λmax], получаем
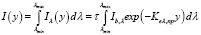 ,
,
где λmin и λmax – границы спектра солнечного излучения (0–3 мкм).
Далее, для изучения зависимости поглощения светового потока солнечного излучения наножидкостью от материала наночастиц проведем вычислительные эксперименты. В расчетах будет рассматриваться ряд наножидкостей, состоящих из одной и той же базовой жидкости, в качестве которой взята дистиллированная вода, но с разными материалами наночастиц.
В качестве материала наночастиц использовались частицы алюминия, серебра, золота и меди. Чтобы обеспечить сравнимость результатов, во всех численных экспериментах использована наножидкость с одинаковой фиксированной объемной долей наночастиц (0,8 %) и их диаметром (5 нм). Для удобства численного эксперимента положим, что падающая на верхнюю часть коллектора интенсивность солнечного излучения суммарно равна 1000 Вт/м2, а коэффициент прохождения излучения через стекло τ = 0.9.
На рис. 3, а–г, представлен результат расчета распространения интенсивности солнечного излучения в НКПП по всей глубине для частиц алюминия, серебра, золота и меди соответственно, которые имели диаметр 5 нм и объемную долю 0,8 %.
Заметим, что полученные результаты моделирования для спектральной интенсивности солнечного излучения, проходящего сквозь коллоидную суспензию, состоящую из дистиллированной воды и наночастиц алюминия, совпали с результатами, представленными в работе [12]. Данный факт подтверждает корректность работы реализованного алгоритма.
Из рис. 3, а–г, видно, что для наножидкостей, использующих дистиллированную воду в качестве базовой жидкости, наибольшим поглощением интенсивности солнечного излучения обладает жидкость с диспергированными в ней наночастицами алюминия, а наименьшим – наножидкость с частицами меди. Из представленных результатов можно резюмировать, что ввиду различных химических свойств наночастицы различных материалов взаимодействуют с базовыми жидкостями по-разному. Это приводит к изменению поглощающих свойств полученных наножидкостей.
Рассмотрим, как размеры наночастиц при сохранении объемной доли влияют на интенсивность светового потока. Для краткости далее будут приведены результаты численных экспериментов только для наножидкостей, в составе которых присутствуют дистиллированная вода и наночастицы алюминия. Объемная доля наночастиц зафиксирована на уровне 0,8 %, а диаметр принимает последовательно значения 1, 5, 10, 15 и 20 нм. Для других типов наножидкостей, которые рассмотрены ранее, наблюдается аналогичная тенденция.
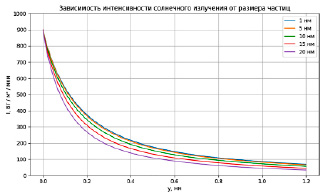
Рис. 4. Распространение интенсивности солнечного излучения в НКПП при различных размерах частиц и объемной доле fv = 0.8% Источник: составлено авторами
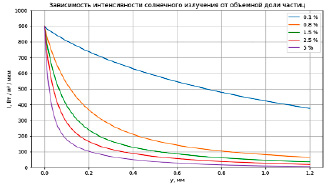
Рис. 5. Распространение интенсивности солнечного излучения в НКПП при различных значениях объемной доли Источник: составлено авторами
На рис. 4 представлены результаты моделирования интенсивности солнечного излучения в НКПП при различных размерах наночастиц алюминия. Из представленных графиков видно, что с увеличением размеров наночастиц поглощение солнечного излучения также увеличивается. Наножидкость с диаметром наночастиц 20 нм обладает наибольшим поглощением, в то время как наножидкость с диаметром наночастиц 1 нм имеет наименьшее поглощение. Этот факт говорит о значительной зависимости показателя поглощения наножидкости от диаметра наночастиц и целесообразности использования более крупных частиц для улучшения переноса тепла.
Далее выполнены расчеты, позволяющие определить зависимость интенсивности потока солнечного излучения от объемной доли наночастиц при постоянном диаметре, равном 5 нм. В данном случае объемная доля наночастиц варьировалась и принимала значения 0,1; 0,8; 1,5; 2,5 и 5 % (рис. 5).
Анализ представленных выше результатов позволяет резюмировать, что увеличение объемной доли наночастиц приводит к увеличению поглощения солнечного излучения. Наблюдается наивысшее поглощение у наножидкости с объемной долей наночастиц 5 %, а наименьшее – у наножидкости с объемной долей 0,1 %. Проведенные расчеты подтверждают прямую зависимость между коэффициентом удельного поглощения светового потока в наножидкости и диаметром, а также объемной долей наночастиц.
Дальнейшее развитие исследований в данной области направлено на применение наножидкостей, содержащих смесь наночастиц различных веществ [15].
Заключение
В статье поставлена и решена задача определения интенсивности солнечного излучения внутри НКПП. Из-за сложной зависимости коэффициентов поглощения и рассеивания света от длины волны спектра солнечного излучения общая задача определения интенсивности потока солнечного излучения внутри НКПП не имеет аналитического решения, поэтому использованы методы вычислительной математики. Получены численные результаты исследования, которые позволили оценить влияние материала, объемной доли и диаметра наночастиц на процессы поглощения солнечного излучения в наножидкости. Расчеты показали, что поглощающие свойства наножидкостей и базовых жидкостей могут значительно отличаться. Выбор наножидкостей с высоким показателем поглощения солнечного излучения в качестве рабочих жидкостей позволяет создавать «тонкие» солнечные коллекторы прямого поглощения.



