Введение
Фармакокинетика (ФК) – ключевая дисциплина в доклинических и клинических исследованиях, изучающая динамику абсорбции, распределения, метаболизма и экскреции (ADME) лекарственных веществ в организме [1, с. 30–31]. В условиях роста затрат на разработку препаратов и ужесточения регуляторных требований, фармакокинетическое моделирование становится незаменимым инструментом для оптимизации процессов создания новых терапевтических агентов [2; 3]. Современные вычислительные методы позволяют прогнозировать поведение лекарств in silico, сокращая время и ресурсы, затрачиваемые на эксперименты in vitro и in vivo. Фармакокинетическое моделирование позволяет добиться оптимизировать и персонализировать дозировки, а также спрогнозировать риск лекарственных взаимодействий [4; 5].
Основными методами моделирования фармакокинетики лекарственного вещества являются компартментные (камерные) модели и физиологически обоснованные (перфузионные) модели.
Компартментные модели основаны на абстрактном представлении организма как системы взаимосвязанных гомогенных камер, где каждая камера символизирует условную часть организма (например, плазма крови, внеклеточная жидкость, ткани с медленным кровотоком или отдельные органы). Ключевое допущение метода – достижение кинетической гомогенности внутри камеры, что подразумевает мгновенное и равномерное распределение препарата в пределах выделенного объема [6]. Математически такие модели описываются системами обыкновенных дифференциальных уравнений (ОДУ), где параметры (константы скоростей переноса, объемы распределения) оцениваются методом наименьших квадратов на основе экспериментальных данных. Преимущество подхода – простота реализации и низкие вычислительные затраты, что делает его популярным для анализа данных I/II фаз клинических испытаний [7].
Физиологически обоснованные модели используют принципиально иную парадигму, воспроизводя анатомо-физиологическую структуру организма. Модель включает реалистичные параметры, что позволяет прогнозировать фармакокинетику с учетом межорганных взаимодействий, пола, возраста и патологий. Например, PBPK-модели успешно применяются для экстраполяции данных с животных на человека и оценки лекарственных взаимодействий [7]. В рамках данной работы используется компартментный подход ввиду его простоты, но при этом достаточной эффективности.
В рамках компартментного подхода к фармакокинетическому моделированию простейшей структурой является однокамерная модель, предполагающая, что весь организм представлен единой гомогенной системой, взаимодействующей с внешней средой через процессы абсорбции и элиминации [8]. Для более детального описания пространственно-временного распределения лекарств используются многокамерные. Камеры при этом не обязательно соответствуют анатомическим структурам, а отражают условные зоны с разной скоростью переноса вещества. Наибольшее практическое значение имеет двухкамерная модель, разделяющая организм на центральную камеру (плазма крови, быстро перфузируемые органы) и периферическую камеру (медленно насыщаемые ткани) [9]. Применяются и модели с большим числом камер.
Целью исследования является совершенствование существующей пятикамерной модели фармакокинетики гибридных наночастиц порфирин-фуллеренового типа с использованием библиотеки PyPharm, основной акцент сделан на повышение точности прогнозирования распределения наночастиц в организме за счет структурной и алгоритмической модификации модели.
Материалы и методы исследования
Моделирование фармакокинетики порфирин-фуллереновых наночастиц (РМС-16)
В качестве материала были выбраны низкотоксичные (ЛД50 = 896 мг/кг, крысы, в/в) порфиринсодержащие наночастицы на основе фуллерена C60 (PMC-16) [10; 11]. Эти частицы способны высвобождать изотоп магния [25Mg2+], который имеет потенциал для снижения тканевой гипоксии различного генеза [11].
Рассматривалось моделирование in silico фармакокинетики порфирин-фуллереновых наночастиц в организме крыс после однократного внутривенного введения. Авторами работы [11] предложена пятикамерная (рис. 1) модель для описания распространения лекарственного вещества в организме, таргетированного для лечения ишемического инсульта. Наночастицы после введения распространяются через кровь и попадают в органы. Константы со знаком «+» отражают процесс доставки вещества в тот или иной орган, а константы со знаком «-» отражают вывод вещества из органа. Так, например, константа kh+ характеризует скорость доставки PMC-16 в сердце, а kh– отвечает за вывод вещества из сердца обратно в кровь. За элиминацию вещества из крови отвечает константа ke, за вывод через печень – kl–. Поскольку PMC-16 проникает с другой скоростью в область инсульта, чем в здоровую область мозга, введение компартмента «межклеточное пространство» позволяет учесть величину поражения мозга при ишемическом инсульте через константу kis+ [12].
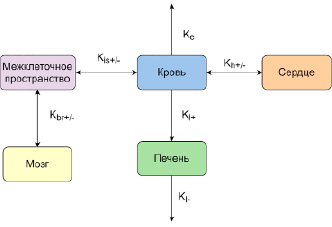
Рис. 1. Пятикамерная модель, описывающая фармакокинетику порфирин-фуллереновых наночастиц в организме крыс Источник: составлено авторами на основе [12]
Модель, предложенная авторами, была описана при помощи системы дифференциальных уравнений:
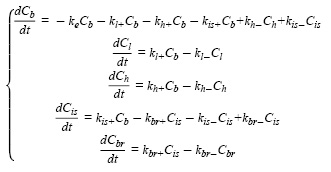, (1)
где Cb, Cl, Ch, Cis, Cbr отражают концентрации наночастиц в крови, печени, сердце, межклеточном пространстве головного мозга и клетках мозга соответственно.
В качестве наборов данных использовались средние значения концентрации PMC-16 в органах – сердце, печени и клетках мозга животного и крови (всего 4 набора данных) в моменты времени t = 0,25; 0,5; 1; 4; 8; 24 ч, при однократном введении в дозе 20 мг/кг. Подробнее данные in vivo эксперимента приведены в [12] (число животных n = 5). Модель авторов приемлемо описывает кривые высвобождения, однако имеет некие недостатки, в большей степени связанные с непопаданием в пики и конечные значения экспериментальных данных. Целью данного исследования была доработка существующей модели с использованием библиотеки PyPharm.
Библиотека для моделирования фармакокинетики PyPharm
В процессе исследования была разработана программная библиотека PyPharm [13], которая предоставляет инструменты для моделирования многокамерных систем и выполнения параметрической оптимизации на основе реальных экспериментальных данных.
Основными особенностями библиотеки являются:
1. Использование методов и объектов классических библиотек, используемых для математических расчетов на языке Python – numpy и scipy.
2. Применение эволюционных алгоритмов, в том числе разработанного в ходе исследования алгоритма взаимодействующих стран для поиска неизвестных параметров моделей [14; 15].
3. Использование частичной njit-компиляции библиотеки numba для ускорения вычислительного процесса.
Для количественной оценки точности модели, а также для подбора параметров при помощи алгоритма взаимодействующих стран была использована функция
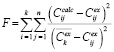, (2)
где k – количество известных наборов данных, n – количество данных в наборе,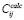 
– вычисленное значение для i-го набора в j-й точке, 
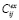– экспериментальное значение для i-го набора в j-й точке, 
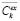– среднее значение по набору экспериментальных данных.
С версии 1.3.0 библиотека поддерживает работу с разделяемой памятью, что позволяет отслеживать процесс оптимизации извне исполняемого кода. Для этого используется специальное имя памяти, хранящееся в поле memory_name модели. Доступ к общей памяти осуществляется через класс ShareableList из модуля multiprocessing, что обеспечивает эффективное взаимодействие между различными процессами.
Все поиски оптимальных параметров моделей были произведены с использованием эволюционного алгоритма взаимодействующих стран, который был вдохновлен классическим генетическим алгоритмом, а также сорняковым и миграционными алгоритмами. В данном алгоритме решения (особи) разбиваются на группы (страны) и в дальнейшем подвергаются последовательности действий, выполняемых либо всей страной, либо отдельными индивидуумами внутри нее. Все действия алгоритма основаны на неких природно-социальных аналогах, таких как размножение, вымирание, война, эпидемия и др. При разработке алгоритм взаимодействующих стран показал свою работоспособность как на тестовых функциях, так и на задачах, связанных с моделированием фармакокинетики [14; 15].
На первом этапе при помощи библиотеки PyPharm была исследована авторская модель с параметрами, указанными в статье [12]. Значение целевой функции (2) для данной модели составило 4.02. Целью использования библиотеки PyPharm было не только сокращение значения целевой функции, но и более эффективная аппроксимация пиковых и конечных экспериментальных значений.
Результаты исследования и их обсуждение
Оптимизация параметров модели с использованием библиотеки PyPharm
На начальном этапе исследования была предпринята попытка использовать исходную авторскую модель без изменений и лишь оптимизировать параметры данной модели. Как и в статье авторов [12], константа элиминации ke была зафиксирована на значении 0,077, однако дополнительно был введен параметр kt, отвечающий за преобразование единиц измерения входной концентрации в единицы измерения выходной концентрации. Этот параметр необходим, поскольку начальная концентрация, полученная из дозы, задается в мг/мл, в этих же единицах проводится расчет, а экспериментальные данные по концентрации в органах [12] приведены в нг/мг белка S125. Оптимизация производилась с использованием класса Magic Compartment Model библиотеки PyPharm. Найденные параметры отражены в табл. 1.
Таблица 1
Значения найденных параметров для исходной модели (1)
|
Название параметра |
Значение |
|
kbr+ |
0,31 |
|
kbr– |
3,42 |
|
kis+ |
0,20 |
|
kis– |
0,14 |
|
kl+ |
1,91 |
|
kl– |
1,34 |
|
kh+ |
1,63 |
|
kh– |
0,50 |
|
kt |
5,14 |
Модель с параметрами, подобранными при помощи алгоритма взаимодействующих стран, существенно превзошла по точности модель с оригинальными настройками (F = 1.35 vs F = 4.02).
На втором этапе была произведена попытка улучшить результаты, учитывая при моделировании объемы камер. Данную модель также можно представить при помощи системы ОДУ:
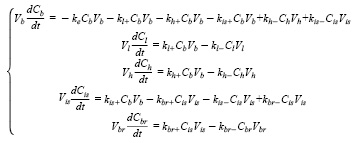. (3)
Таблица 2
Значения найденных параметров для модели (3), учитывающей объемы камер
|
Название параметра |
Значение |
|
kbr+ |
1,08 |
|
kbr– |
3,68 |
|
kis+ |
0,60 |
|
kis– |
1,03 |
|
kl+ |
0,17 |
|
kl– |
6,37 |
|
kh+ |
0,53 |
|
kh– |
3,06 |
|
kt |
77,48 |
|
Vb |
57,11 |
|
Vl |
1,14 |
|
Vh |
5,74 |
|
Vis |
249,38 |
|
Vbr |
235,52 |
При изменении модели добавилось пять новых неизвестных, представляющих собой объемы камер. Поиск параметров модели, учитывающей объемы камер, также производился при помощи алгоритма эволюционных стран (табл. 2).
Модель, учитывающая объемы камер, улучшила значение целевой функции, но не существенно (F = 1.25). Сравнение результатов работы различных моделей приведено на рис. 2–4, которые отображают зависимости концентрации лекарственного вещества в том или ином органе от времени.
Полученные после оптимизации модели описывают данные значительно лучше исходной (значение целевой функции уменьшилось примерно на 67 %), однако проблема с непопаданием модели в максимум и в конечное значение осталась актуальной. Более того, алгоритм взаимодействующих стран подобрал значения так, что оптимизировал в основном именно те точки, которые находились в середине временного промежутка.
На следующем этапе были предложены 2 новые оригинальные модели, которые по предположениям должны были более реалистично учитывать накопление лекарственного вещества в органах. По задумке каждая камера получает дублирующую, с которой она связана входящим и выходящим потоками (4), где значения с индексом d – камеры-дублера. При этом были рассмотрены 2 варианта, когда экспериментальные данные аппроксимируются значениями из основных камер и из их дублеров.
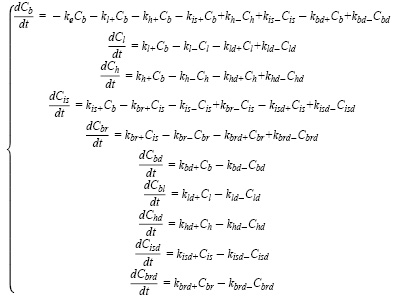. (4)
Таблица 3
Значения найденных параметров для модели, учитывающей объемы камер и камеры-дублеры
|
Название параметра |
Значение для аппроксимации основными камерами |
Значение для аппроксимации камерами-дублерами |
|
kbr+ |
1,46 |
2,19 |
|
kbr– |
0,06 |
0,46 |
|
kis+ |
0,02 |
0,15 |
|
kis– |
0,39 |
5,23 |
|
kl+ |
1,35 |
7,78 |
|
kl– |
0,09 |
3,62 |
|
kh+ |
1,03 |
4,68 |
|
kh– |
5,49e-3 |
7,43e-4 |
|
kbrd+ |
0,53 |
2,18 |
|
kbrd– |
0,15 |
0,55 |
|
kisd+ |
2,96 |
9,98 |
|
kisd– |
9,68 |
10 |
|
kld+ |
2,5 |
2,22 |
|
kld– |
.0,19 |
9,87 |
|
khd+ |
1,23 |
3,49 |
|
khd– |
0,38 |
0,39 |
|
kbd+ |
0,12 |
3,37e-3 |
|
kbd– |
10 |
9,94 |
|
kt |
8,10 |
10,53 |
Таким образом в модель добавляется еще 10 неизвестных параметров, представляющих собой константы скорости в камерах-дублерах. По результатам оптимизации были получены следующие данные (табл. 3).
При этом значения целевой функции для разных вариантов выбора аппроксимирующих камер составили F = 0,90 и F = 1,37 соответственно для вариантов с основными и с камерами-дублерами. Графически результаты отображены на рис. 5–7.
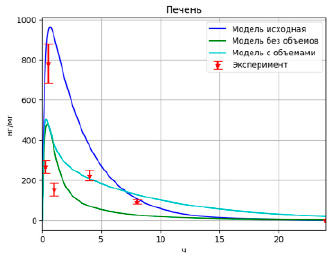
Рис. 2. Результаты моделирования высвобождения PMC-16 в печени
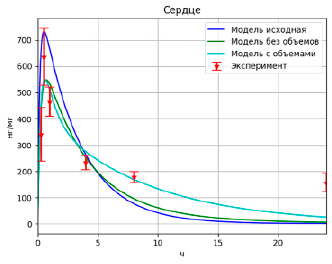
Рис. 3. Результаты моделирования высвобождения PMC-16 в сердце
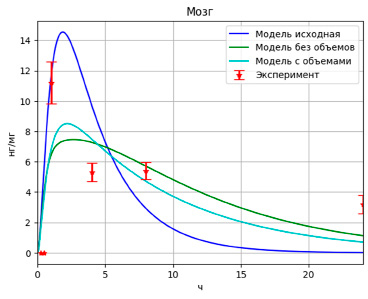
Рис. 4. Результаты моделирования высвобождения PMC-16 в мозге
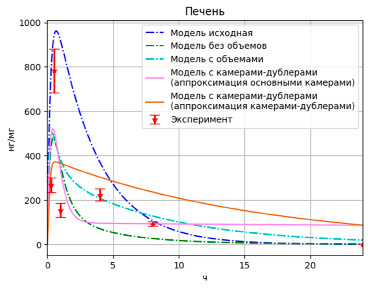
Рис. 5. Результаты моделирования высвобождения PMC-16 в печени с учетом дублирующих камер
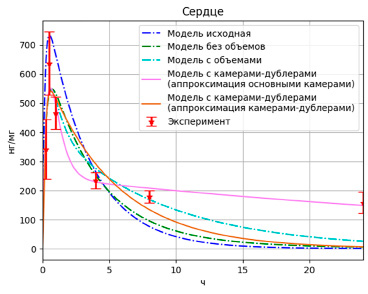
Рис. 6. Результаты моделирования высвобождения PMC-16 в сердце с учетом дублирующих камер
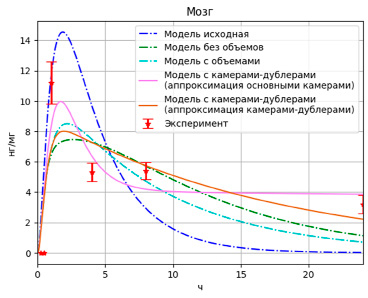
Рис. 7. Результаты моделирования высвобождения PMC-16 в мозге с учетом дублирующих камер
Таблица 4
Значения найденных параметров для модели, учитывающей объемы камер, камеры-дублеры, а также весовые коэффициенты данных
|
Название параметра |
Значение |
|
kbr+ |
0,05 |
|
kbr– |
14,18 |
|
kis+ |
3,08 |
|
kis– |
0,23 |
|
kl+ |
1,53 |
|
kl– |
0,12 |
|
kh+ |
1,70 |
|
kh– |
1,16 |
|
kbrd+ |
25 |
|
kbrd– |
10,88 |
|
kisd+ |
0,79 |
|
kisd– |
25 |
|
kld+ |
1,94 |
|
kld– |
1,06e-3 |
|
khd+ |
24,03 |
|
khd– |
24,76 |
|
kbd+ |
24,76 |
|
kbd– |
24,56 |
|
kt |
20,27 |
Можно заметить, что вариант модели с камерами-дублерами, где данные аппроксимируются основными камерами, наилучший не только по значению целевой функции (F = 0,9), но и по аппроксимации конечных значений. При этом данная модель плохо аппроксимирует пиковые значения, особенно для данных по печени.
Библиотека PyPharm позволяет варьировать значимость теоретических данных при оптимизации параметров модели, что позволило взять за основу полученную на прошлом этапе модель и улучшить ее аппроксимирование пиковых значений за счет варьирования весовых коэффициентов у данных. Были получены следующие параметры модели (табл. 4).
Результаты моделирования отражены на рис. 8–10.
Как видно из графиков (рис. 8–10), несмотря на то, что значение целевой функции выросло (F = 1,81), данная модель более точно описывает одновременно и пиковые значения и конечные.
Для более тщательного изучения эффективности применения алгоритма взаимодействующих стран, а также использования новой модели с учетом камер-дублеров были проанализированы значения относительных ошибок для каждой из моделей (табл. 5).
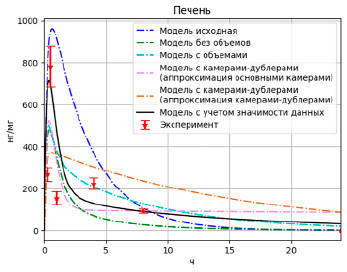
Рис. 8. Результаты моделирования высвобождения PMC-16 в печени с учетом значимости данных
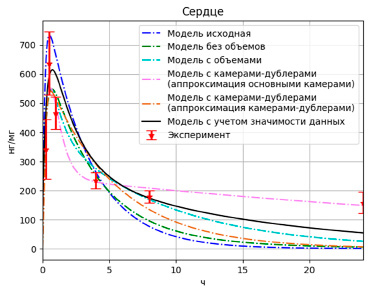
Рис. 9. Результаты моделирования высвобождения PMC-16 в сердце с учетом значимости данных
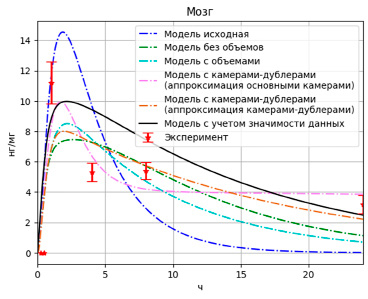
Рис. 10. Результаты моделирования высвобождения PMC-16 в мозге с учетом значимости данных
Таблица 5
Значение показателя абсолютной ошибки для различных моделей
|
Максимальное значение абсолютной ошибки (Мозг/Печень/Сердце) |
Минимальное значение абсолютной ошибки (Мозг/Печень/Сердце) |
Среднее значение абсолютной ошибки (Мозг/Печень/Сердце) |
|
|
Исходная модель |
5,7 / 764,7 / 288,4 |
0,3 / 0,76 / 28,1 |
3,0 / 257,9 / 145,1 |
|
Оптимизированная модель без объемов |
4,8 / 305,7 / 152,8 |
0,3 / 1,8 / 16,8 |
2,5 / 147,1 / 82,2 |
|
Оптимизированная модель с объемами |
4,5 / 298,0 / 132,8 |
0,7 / 16,9 / 10,2 |
2,5 / 135,4 / 68,5 |
|
Модель с камерами- дублерами (аппроксимация основными камерами) |
4,2 / 270,0 / 93,4 |
0,7 / 0,4 / 5,9 |
2,0 / 144,3 / 40,6 |
|
Модель с камерами-дублерами (аппроксимация камерами-дублерами) |
4,4 / 413,4 / 151,7 |
0,3 / 40,2 / 44,8 |
2,1 / 162,1 / 76,8 |
|
Модель с учетом значимости данных |
5,8 / 389,0 / 133,2 |
0,7 / 2,4 / 5,4 |
3,0 / 154,2 / 78,6 |
Данные из табл. 5 подтверждают эффективность использования библиотеки PyPharm, кроме того, подтверждается и эффективность внедрения камер-дублеров.
На основе результатов работы можно сделать вывод, что использование камер-дублеров позволяет существенно повысить качество предсказания фармакокинетической модели в случае, когда фармакокинетические кривые стремятся к постоянному ненулевому значению, то есть имеет место накопление вещества в тканях. При этом органам соответствуют именно основные камеры. В противном случае качество модели значительно снижается. Камеры-дублеры, таким образом, имитируют окружающие орган ткани, где лекарственный препарат или наночастицы могут находиться длительное время, поддерживая почти постоянный уровень лекарства в основной камере органа в течение долгого времени.
Заключение
В данной статье для решения задач фармакокинетики фуллерен-порфиринового нанофармакофора PMC-16 был применен новый алгоритм, основанный на моделях популяционной динамики. Алгоритм был применен как встроенный метод библиотеки PyPharm, разработанной для построения фармакокинетических моделей. Библиотека продемонстрировала свою гибкость настройки по отношению к возможностям построения моделей, а также значимости отдельных экспериментальных данных.
Была предложена новая модель для описания фармакокинетики фуллерен-порфиринового нанофармакофора PMC-16, использующая концепцию камер-дублеров. Данная модель продемонстрировала свою эффективность и продемонстрировала наименьшее значение целевой функции (F = 0,9).
Результаты, полученные алгоритмом, превзошли по точности результаты исходного исследования авторов (приблизительно в 4,5 раза), помимо этого полученные модели более точно аппроксимировали пиковые и конечные значения кривых высвобождения. Кроме того, библиотека PyPharm (в частности, алгоритм взаимодействующих стран) показала свою эффективность для моделей с большим количеством неизвестных параметров.