Введение
Металлы и сплавы с высокой степенью очистки находят применение в различных отраслях промышленности [1]. Одной из перспективных технологий получения чистых металлов является плавление во взвешенном состоянии [2]. Несмотря на то, что этот способ бесконтактного плавления металлов был предложен больше века назад (Отто Мук, 1923 г.), широкого распространения в промышленности он так и не получил. Это связано в первую очередь с высокой энергозатратностью процесса, а также проблемой стабилизации положения расплавляемого металла в индукторе [3]. Решение задачи стабилизации положения расплава в индукторе достижимо путем включения в технологический процесс плавления во взвешенном состоянии системы стабилизации расплава [4]. Для создания такой системы необходимо учитывать характер воздействия электромагнитного поля на расплавляемый металл, при этом прямое измерение напряженности поля в различных точках индуктора не представляется возможным. Применение современных методов численного моделирования позволяет оценить воздействие переменного электромагнитного поля на нагреваемый образец с учетом его размеров, положения в индукторе и свойств металла.
Цель исследования заключается в разработке численного метода оценки неоднородности электромагнитного поля, создаваемого коническим индуктором, и его влияния на стабилизацию расплава при плавке во взвешенном состоянии, а также в решении следующих задач:
1) анализ распределения напряженности магнитного поля в зависимости от геометрии и положения образца;
2) установление численного значения коэффициента неоднородности, характеризующего конфигурацию электромагнитного поля.
Материалы и методы исследования
Воздействие высокочастотного переменного магнитного поля на металл приводит к возникновению в нем вихревых токов (токов Фуко), которые вытесняют поле из пространства, занимаемого металлом [5, 6]. В результате этого в переменном магнитном поле неферромагнитный проводник ведет себя как диамагнетик в постоянном поле. Силовое взаимодействие токов Фуко и магнитного поля выталкивает металл из области с большей плотностью в область с меньшей плотностью поля, называемую потенциальной ямой [7]. Если величина выталкивающей силы достаточно велика (больше или равняется силе тяжести, действующей на образец металла), то металл удерживается во взвешенном состоянии [8, 9].
Воздействие электромагнитного поля на металл можно описать как сумму воздействий электромагнитной силы (F) и поглощенной металлом мощности (ps), которая идет на его нагревание. Данное условие описывается формулой
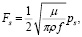 (1)
(1)
где Fs – электромагнитная сила, действующая на единицу поверхности металла [Н]; μ – магнитная проницаемость среды; ρ – электрическое сопротивление металла; f – частота электромагнитного поля, ps – мощность, передаваемая металлу, отнесенная к единице его поверхности.
Устойчивое поддержание образца металла во взвешенном состоянии достижимо только в неоднородном магнитном поле [10]. При этом характер воздействия поля на металл может быть учтен введением коэффициента А, описывающего конфигурацию магнитного поля, окружающего лимитируемый образец. Введение коэффициента А было предложено А.А. Фогелем [11] для описания геометрической характеристики электромагнитного поля, воздействующего на образец металла. В таком случае выражение (1) примет вид, представленный в формуле
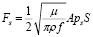 , (2)
, (2)
где S – площадь поверхности металла, А – коэффициент, зависящий исключительно от конфигурации поля у поверхности металла, может быть различным в зависимости от таких условий, как положение образца относительно индуктора, геометрии образца и геометрии самого индуктора Так, например, при левитации образца в форме диска над компланарным индуктором поле оказывает давление только с одной стороны, при этом величина A ≈ 1. При всестороннем обжатии образца полем значение коэффициента А достигает минимального значения (A → 0), в том случае, когда образец полностью окружен однородным полем. Мощность, сообщаемая единице поверхности, выражается формулой
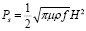 , (3)
, (3)
где H – напряженность магнитного поля, воздействующего на образец.
В результате решения системы уравнений Максвелла для образца в продольном плоскопараллельном магнитном поле установлена зависимость магнитной составляющей поля от его частоты для условия
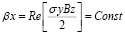 . (4)
. (4)
Таким образом, при фиксированном размере металлического образца существует определенный диапазон частот f, при которых металл левитирует в электромагнитном поле. Определение конкретного значения частоты тока для обеспечения состояния левитации определяется электрическим сопротивлением металла и его положением в индукторе [12, 13].
Отсюда следует, что задача стабилизации положения образца в индукторе может быть сведена к поиску конфигурации электромагнитного поля (значений частоты и силы тока в индукторе), при которой равнодействующая силы тяжести и силы Лоренца, действующих на образец, будет стремиться к нулю [14, 15].
Параметры численной модели индуктора
|
Параметр |
Значение |
|
Сопротивление проводника индуктора (медь), Ом |
0,0128 |
|
Сопротивление образца (алюминий), Oм |
0,028 |
|
Магнитная проницаемость проводника индуктора (медь), Гн/м |
1.257∙10−6 |
|
Магнитная проницаемость образца (алюминий), Гн/м |
1.257∙10−6 |
|
Магнитная проницаемость среды (воздух), Гн/м |
1.257∙10−6 |
|
Частота тока в индукторе, Гц |
50000 |
|
Сила тока в индукторе, А |
470 |
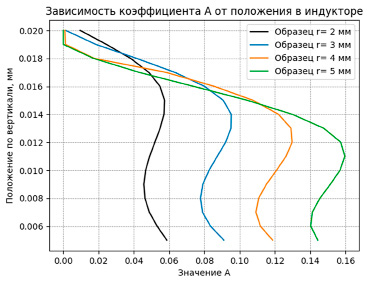
Графики зависимостей значений коэффициента А от положения в индукторе по вертикали для образцов алюминия разных радиусов
Для определения значения коэффициента неоднородности электромагнитного поля А из выражения (2) разработана численная модель напряженности электромагнитного поля индуктора на основе метода конечных элементов (МКЭ). Модель включает в себя геометрию конического индуктора из 5 витков и 1 противовитка и образец металла. Для ускорения расчетов модель выполнена двухмерной и описывает распределение напряженности электромагнитного поля в плоскости оси симметрии индуктора. Данное допущение было принято исходя из симметрии конструкции индуктора. Построение численной модели осуществлялось в программном комплексе Agros2D. Параметры численной модели приведены в таблице.
Результаты исследования и их обсуждение
Для установления зависимости коэффициента А от изменения положения в индукторе была проведена серия расчетов напряженности магнитного поля индуктора в численной модели. В рамках эксперимента варьировались положение и размеры образцов алюминия в индукторе при неизменной частоте и силе тока.
В ходе виртуального эксперимента в численной модели изменялись положение относительно плоскости основания конического индуктора (противовитка) в диапазоне от 0 до 20 мм с шагом 1 мм и размеры алюминиевых образцов в индукторе при фиксированной частоте 50 кГц и силе тока 470 А.
Модель была разработана с учетом физических свойств (электрическое сопротивление и магнитопроницаемость) алюминия и материала индуктора (медь). Для каждого образца, имеющего радиус от 2 до 5 мм, и в каждой точке рассчитывались распределение напряженности электромагнитного поля и величина силы Лоренца, действующей на образец металла.
Численное значение коэффициента А вычислялось из полученной в результате моделирования величины силы Лоренца по формуле
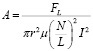 , (5)
, (5)
где A – коэффициент неоднородности электромагнитного поля индуктора, зависящий от геометрической конфигурации поля вокруг образца; FL – выталкивающая сила Лоренца, действующая на единицу объема металла, обусловленная взаимодействием индукционных токов в образце с внешним магнитным полем; I – сила тока в индукторе, r – радиус образца, N – количество витков индуктора; L – длина проводника индуктора, μ – магнитная проницаемость материала образца.
На рисунке представлены графики изменения значения коэффициента А от положения в индукторе для образцов алюминия различных размеров.
На основе представленного графика на рисунке можно сделать вывод, что зависимость коэффициента A от положения образцов в индукторе варьируется для образцов с разными радиусами (r). С увеличением радиуса образца максимальные значения коэффициента A достигаются в более низких областях индуктора, что объясняется изменением распределения неоднородности электромагнитного поля в зависимости от размера образца. Области с наибольшими значениями, соответствующими коэффициенту, соответствуют областям потенциальных ям для образцов соответствующих размеров. Это говорит о том, что для образцов с разными радиусами существуют оптимальные зоны удержания в индукторе, где влияние электромагнитных сил наиболее эффективно для стабилизации их положения. При увеличении радиуса образца центр такой области смещается вниз, что следует учитывать при настройке параметров плавки во взвешенном состоянии.
Заключение
В данной работе был предложен метод, позволяющий на основе численной модели определить значение коэффициента неоднородности электромагнитного поля, создаваемого коническим индуктором при плавке металлов во взвешенном состоянии. В ходе исследования установлены зависимости коэффициента неоднородности электромагнитного поля от положения расплавляемого образца в индукторе и его размеров, что позволяет более точно прогнозировать характер воздействия поля на образец металла. Полученные зависимости демонстрируют влияние положения образца на характеристики поля, что является ключевым аспектом для разработки эффективных систем управления левитационной плавкой металлов.
Результаты исследования могут быть интегрированы в систему управления процессом, что способствует повышению стабильности и эффективности плавки, а также позволяет оптимизировать расход энергии. Перспективы дальнейших исследований направлены на экспериментальную апробацию полученных зависимостей и их применение для динамического регулирования технологических режимов в зависимости от изменений в процессе плавки, что обеспечит повышение качества конечного продукта и расширение возможностей использования метода в промышленном производстве.



