Введение
В последние годы наблюдается рост интереса к проблеме недостаточной подготовленности студентов технических вузов по математике. Успех в обучении математике требует не только базовых знаний и навыков, полученных в школе, но и глубокого понимания теоретических аспектов, таких как логические рассуждения, умение строить доказательства и структурировать собственные рассуждения. Однако студенты часто демонстрируют существенные пробелы в понимании фундаментальных математических концепций, что приводит к систематическим ошибкам и затрудняет усвоение материала на более высоком уровне. В контексте обучения математике остаточные знания – это те базовые знания, умения, навыки и понимание, которые остаются после завершения школьного курса.
Анализ остаточных знаний студентов – это критически важный аспект оценки их реальной математической подготовки после школы, особенно в контексте перехода к изучению высшей математики в вузе. Значение анализа остаточных знаний можно подчеркнуть следующими аспектами.
– Изучение остаточных знаний позволяет увидеть, насколько знания студентов соответствуют требованиям, предъявляемым в вузах, и понять, насколько они способны применять школьные знания в новой академической среде.
– Анализ ошибок и пробелов, возникающих у студентов после сдачи ЕГЭ, дает возможность увидеть, какие темы и навыки остаются неусвоенными. Это позволяет оценить, какие разделы школьной программы требуют доработки или изменения, чтобы лучше подготовить выпускников к обучению в вузах.
– Исследование остаточных знаний помогает выявить систематические ошибки, которые наблюдаются у студентов, и лучше понять их природу. Зная эти пробелы, преподаватели могут скорректировать учебные планы или предложить вводные курсы, чтобы восполнить эти недостатки.
– Анализ остаточных знаний помогает учителям и преподавателям понять, какие методы обучения могут быть неэффективными, что позволяет улучшить образовательные стратегии в школах и вузах.
Ключевым методом для выявления остаточных знаний студентов является анализ ошибок, совершаемых студентами при решении задач, так как они показывают, какие знания были усвоены на глубоком уровне, а какие – только формально. Кроме того, исследование ошибок как методический инструмент предлагает пути для улучшения качества математического образования.
Вопросы анализа, классификации, способов устранения математических ошибок студентов, а также их восприятия обучающимися привлекали внимание многих исследователей. В статье [1] А.А. Хаертдинова, анализируя уровень остаточных знаний, указывает на то, что для выравнивания неоднородного уровня начальной подготовки требуется значительно больше времени для аудиторной работы. В.А. Тестовым, Е.А. Перминовым в работе [2] подчеркнуто, что качественная математическая подготовка обеспечивает не только формирование у студентов общих трансдисциплинарных представлений, но и овладение общекультурной когнитивной стратегией в решении профессиональных задач. Большое внимание анализу типичных ошибок уделено в исследованиях В.А. Далингера (см., например, [3]). В работах [4] и [5] на примере тригонометрических функций проведена классификация ошибок на концептуальные и процессуальные. Тема анализа и классификации математических ошибок привлекала и привлекает внимание многих зарубежных ученых. Отметим диссертационную работу K.J. Geuther [6], в которой проведено исследование ошибок студентов при изучении дифференциального исчисления в рамках конструктивистского подхода. В работе [7] автор предлагает использовать ошибки для побуждения студентов к исследованию и решению проблем. В исследовании [8] большое внимание уделено учету эмоционального состояния студента в случае совершения им ошибки.
Проблема анализа систематических ошибок обучающихся при изучении высшей математики остается крайне актуальной, особенно в условиях перехода на новые формы обучения, включая дистанционное. Анализ систематических ошибок студентов позволяет выявить в их подготовке слабые места, которые могут быть неочевидны в стандартном учебном процессе. Это особенно важно в технических вузах, где успешное изучение профильных дисциплин тесно связано с прочными базовыми знаниями по математике. Актуальность данного исследования обусловлена также необходимостью обновления школьной программы, так как многие учащиеся не имеют достаточного уровня подготовки для успешного обучения в вузах.
В данной работе рассмотрены проблемные для студентов важные при изучении высшей математики в вузах разделы элементарной математики, в которых студенты часто совершают систематические ошибки. Систематические ошибки возникают вследствие недостаточного или неверного понимания определенных понятий, принципов или правил. Они имеют устойчивый, повторяющийся характер и часто связаны с пробелами в базовых знаниях. Систематические ошибки обычно вызваны недостаточной проработкой определенных тем, неправильно усвоенными концепциями или ошибочными стратегиями, которые применяет обучающийся. Например, студент может не понимать правила раскрытия модуля и регулярно ошибаться в задачах, связанных с этой темой.
В последние годы в образовательном пространстве России идет динамичное изменение и обновление стандартов как школьного, так и высшего образования. С одной стороны, наблюдается стремление охватить в школьной программе по математике максимальное количество тем, включая и разделы, которые ранее изучались только в высшей школе. С другой стороны, практика обучения математики в вузах показывает нарастание числа ошибок, носящих систематический характер. Один из продуктивных путей разрешения этого несоответствия связан с изучением достигнутого, реального уровня математических знаний студентов после окончания средней школы. Данное исследование выделяет ключевые темы (дроби, модули, упрощения алгебраических выражений, элементарные функции и их свойства).
Целями работы являются проверка остаточных знаний по математике у студентов-первокурсников и определение уровня владения некоторыми разделами элементарной математики, являющимися важными в усвоении высшей математики.
Материалы и методы исследования
Выбрана целевая группа студентов первого курса Казанского государственного архитектурно-строительного университета в количестве 129 студентов.
Сбор и анализ остаточных знаний проводились в соответствии со следующими этапами. Первый этап – это разработка проверочных материалов, которые представляют собой тесты, опросные листы, содержание которых соответствует разделам изучаемых дисциплин. Второй этап – контрольное тестирование или иной срез знаний, проводимые в условиях ограниченного времени под наблюдением преподавателя. Третий этап – проверка выполненных работ контрольного тестирования. Четвертый этап – оценивание выполненного задания контрольного тестирования с проставлением результатов в оценочную ведомость. Пятый этап – обсуждение результатов остаточных знаний в педагогическом коллективе. Шестой этап – использование полученных результатов для коррекции методических и дидактических материалов и рекомендаций в целях повышения уровня остаточных знаний.
Содержание теста следующее (в тесте фигурирует параметр к, который является числом месяца рождения респондентов):
1. Решить неравенство:
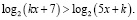
2. Решить неравенство:
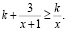
3. Решить уравнение:
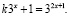
4. Решить уравнение:
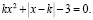
5. Упростить выражение:
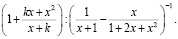
В ходе исследования были использованы методы сравнительного анализа, качественного (описание типов ошибок и характерных примеров ошибок) и количественного анализа (процентное распределение ошибок).
Результаты исследования и их обсуждение
По результатам экспериментов студенты были разбиты на три группы: первая – полностью справились с заданиями, вторая – совершили ошибки или не полностью решили задания, третья – не приступали к решению.
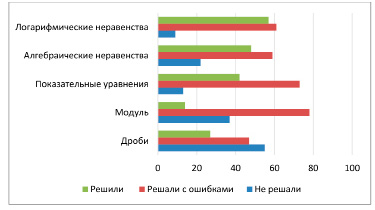
Рис. 1. Диаграмма распределения числа студентов при выполнении пяти заданий теста на группы: не решили, решили с ошибками и решили
При работе с дробями (задание 5) получены следующие результаты: 27 студентов решили задание полностью, 47 совершили ошибки, а 55 не решали задание.
При работе с модулем (4-е задание) получены результаты: 14 студентов решили полностью, 78 – не полностью или с ошибками, 37 – не приступили к его решению.
Показательные уравнения решили 42 студента, 73 совершили ошибки или не довели решение до конца, а 13 к задаче не приступали.
Алгебраические неравенства смогли решить 48 студентов, 59 студентов совершили ошибки, а 22 – не решали вообще.
При работе с логарифмическими неравенствами результат лучше: так, 57 студентов полностью его решили, 61 – допустили ошибки, а только 9 студентов не приступали к его решению.
Для наглядности представим эти результаты в виде диаграммы (рис. 1).
Как видно из диаграммы, наиболее сложным заданием для студентов оказалась задача с модулем, с ней справились только примерно 11% от всех опрошенных. Задачи с модулем пугают школьников, в ЕГЭ они, как правило, встречаются во второй части там, где задание с параметром. Знакомство с понятием абсолютной величины (модулем) происходит еще в 9-м классе, но к 11-му классу модуль уже присутствует в сложных задачах. По результатам тестирования чуть больше 60% респондентов пробовали решать задачи с ним. Но и те, кто правильно раскрыли модуль, получив решения, совершили ошибки. Например, при решении уравнения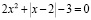 
правильно переходят к совокупности систем:
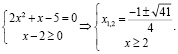
Записывают в ответ оба корня:
,
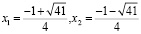хотя очевидно, что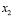 
не подходит. Решая аналогично вторую систему:
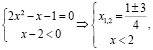
в ответ также записывают оба корня: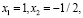 
которые удовлетворяют ограничению. Таким образом, формально разбивая задачу на две, в ответ также записывают все четыре получившихся корня, не учитывая при этом ограничения, полученные при раскрытии модуля. К систематическим ошибкам здесь следует отнести неправильное понимание условий раскрытия модуля, а также объединение решений систем уравнений.
Следующий объект – это задача на упрощение дробных выражений. Чуть менее 21% опрошенных справились с задачей упрощения дроби, а 42,6% к преобразованию не приступили. Приведем типичные ошибки с дробями, полученные в работах. Необходимо упростить дробь
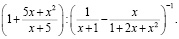
На рисунке 2 представлено решение этой задачи одним из студентов.
Рис. 2. Пример решения задачи на упрощение
Видно, что в первой и во второй скобках студент привел слагаемые к общему знаменателю, а также справился с тем, что при делении на обратную дробь получаем умножение на исходную. Однако дальше студент не смог провести упрощающие преобразования с полученными дробями. Замечено, что громоздкие выражения на упрощение у студентов вызывают негативные эмоции, и они часто отказываются или прекращают в этих случаях преобразовывать алгебраические выражения. Алгебраическое неравенство не содержало громоздкие дроби, к этому заданию приступило большее число студентов, примерно 83%, из них 37,2% полностью с заданием справились, остальные либо неправильно преобразовали дробь, либо некорректно применили метод интервалов, записывая корни как ответ или неверно находя интервалы, подходящие к знаку неравенства (рис. 3), либо совершили ошибки при вычислении корней многочленов в числителе и знаменателе дроби.
Рис. 3. Пример решения алгебраического неравенства
К систематическим ошибкам, кроме перечисленных выше, можно отнести ошибки, связанные с непониманием того, что деление на дробь эквивалентно умножению на ее обратную.
При решении показательных уравнений 32,5% студентов успешно их решили, однако и ошибок совершили 55,6% приступивших к заданию студентов, тем самым показав слабое владение этими математическими объектами. В ходе решения показательных уравнений студенты пренебрегают тем фактом, что показательная функция принимает только положительные значения, что является систематической ошибкой.
Аналогично обстоит дело и с логарифмами. Несмотря на то что процент решенных задач по этому заданию выше, чем у остальных задач (он составляет почти 44,2%), все же число ошибочных решений больше и составляет 47%. Несмотря на выученную технику решения логарифмических неравенств, ограничения на аргумент логарифма студенты не накладывают либо забывают это делать.
Ниже приведен пример решения логарифмического неравенства (рис. 4).
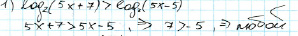
Рис. 4. Пример ошибки при решении логарифмической функции
Систематическая ошибка в решении данного неравенства состоит в том, что не учтены области существования каждого из логарифмов.
Анализ решений показательных и логарифмических уравнений показывает, что студенты не владеют понятием функции вообще и понятиями показательной и логарифмической функций в частности.
Студенты испытывали особенно серьезные затруднения при работе с модулями и показательными функциями, где большинство ошибок носило систематический характер, отражая фундаментальные пробелы в знаниях математики. Замечено при этом, что средний балл ЕГЭ у тестируемых студентов составлял 71 балла, то есть большая часть студентов должна была справиться с заданиями, чего на самом деле не произошло, хотя со времени сдачи ЕГЭ прошло всего несколько месяцев. Хотя данное исследование не имело целью изучение когнитивных трудностей, тем не менее были явно видны недостатки логического мышления и восприятия абстрактных математических объектов.
Эти результаты подтверждают выводы, сделанные в работах Далингера [3], о необходимости более тщательной проработки базовых математических понятий, систематического анализа ошибок и коррекции методов преподавания.
Проведенный анализ ошибок показывает, что, несмотря на успешную сдачу ЕГЭ, многие студенты демонстрируют пробелы в ключевых темах, таких как дроби, модули, логарифмы и показательные функции. Это указывает на то, что знание этих тем, часто поверхностное и направленное на решение стандартных задач ЕГЭ, не всегда переносится на более сложные и теоретически насыщенные задания, требующие гибкости мышления и глубины понимания.
Анализ остаточных знаний студентов показывает, что школьная подготовка часто направлена на успешное решение типичных задач, встречающихся в ЕГЭ, и на овладение конкретными шаблонами решений. Это приводит к тому, что многие студенты могут успешно решать задачи на экзамене, но оказываются не способными применять полученные знания в вузе. Анализ ошибок показывает, что многие студенты не усвоили базовые понятия (функции, свойства степенных, показательных, тригонометрических функций) и принципы работы с ними. Ошибки студентов указывают на формальный характер многих знаний, с которыми они пришли в вуз. Вместо того чтобы понимать суть математических понятий и свойств функций, студенты часто механически воспроизводят методы решения задач. При отсутствии (в массовом порядке) фундаментальных, необходимых знаний, касающихся в том числе умения преобразовывать, упрощать алгебраические выражения, лежащих в основе математики в вузе, возникает вопрос о целесообразности изучения в школе (не специализированной) разделов математического анализа, элементов теории вероятности и финансовой математики.
Выводы
На основе полученных результатов можно сформулировать следующие выводы.
1. Проведенные эксперименты показывают, что остаточные знания в целом не соответствуют баллам, полученным в результате единых государственных экзаменов. Систематические ошибки являются основным препятствием для студентов в освоении высшей математики. Особые трудности вызывают темы с модулями, логарифмами и показательными функциями. У студентов отсутствует четкое понимание как самого понятия функции, так и ограничений на функции (области определения и свойства элементарных функций), что ведет к многочисленным ошибкам.
2. Выявленные проблемы свидетельствуют о необходимости пересмотра школьной программы по математике. Фокус, с точки зрения авторов статьи, следует сместить на качественное освоение базовых тем (таких как дроби, преобразование алгебраических выражений, функции, модули).
3. Для улучшения математической подготовки студентов нужны дополнительные занятия или курсы в вузах по элементарной математике для укрепления базовых знаний.