Введение
Интеграция функциональной, в том числе математической, грамотности в систему основного общего образования ставит ряд вопросов об организации образовательного процесса и поиска соответствующих подходов, методик и технологий. В отличие от процесса освоения традиционного математического содержания, например ряда вопросов алгебры, решение заданий на оценку математической грамотности не является алгоритмичным. Такие задания являются уникальными. В них описывается реальная жизненная ситуация и требуется ее перевод на математический язык. Для решения заданий по математической грамотности могут применяться различные способы решения, основанные зачастую не только на строгих математических рассуждениях, приводящих к однозначному решению, но и на практических соображениях с подбором адекватного математического инструментария. При этом результат может носить приближенный или оценочный характер. Таким образом, процесс формирования математической грамотности предполагает развитие у обучающихся критического мышления [1; 2, с. 23; 3, с. 17].
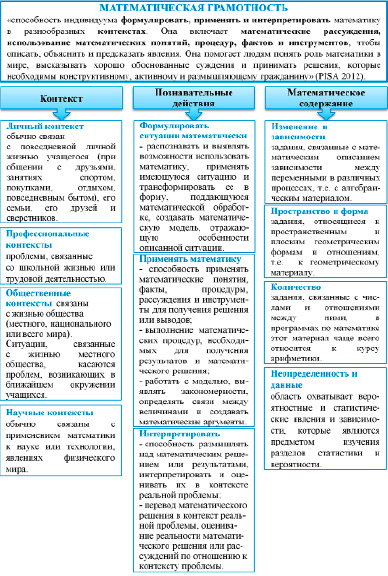
Рис. 1. Модель формирования математической грамотности
По мнению Дж. Браус и Д. Вуд, критическое мышление рассматривается как поиск здравого смысла, то есть «как рассудить объективно и поступить логично с учётом как своей точки зрения, так и других мнений, умение отказаться от собственных предубеждений. Критические мыслители способны выдвинуть новые идеи и увидеть новые возможности, что весьма существенно при решении проблем» [4, с. 9].
Д. Халперн в своей работе «Психология критического мышления» определяет критическое мышление следующим образом: это «направленное мышление, оно отличается взвешенностью, логичностью и целенаправленностью, его отличает использование таких когнитивных навыков и стратегий, которые увеличивают вероятность получения желательного результата» [5, с. 56].
Процесс развития критического мышления предполагает соотнесение внешней информации с теми знаниями, которые имеются у человека, с последующей выработкой решений о том, что можно принять, что необходимо дополнить, а что – отвергнуть [6, с. 16; 7; 8, с. 24]. Этот процесс согласуется с моделью формирования математической грамотности (рис. 1), которая основана на освоении познавательных действий: формулировать, применять и интерпретировать [9, с. 11]. Их совокупность позволяет посредством рассуждений распознавать математику в реальной ситуации, применять математический аппарат для ее разрешения и интерпретировать полученный математический результат на языке реальной ситуации [10; 11].
Цель исследования состоит в описании возможностей применения технологии развития критического мышления в процессе формирования математической грамотности обучающихся основной школы.
Материал и методы исследования
Материал и методы исследования: анализ литературных источников, эффективных образовательных практик и ресурсной базы формирования функциональной грамотности, проектирование, практическое моделирование, синтез, обобщение, описание.
Результаты исследования и их обсуждение
Процесс формирования математической грамотности может быть основан на использовании технологии развития критического мышления (ТРКМ). Это позволит не только анализировать информацию, но и определять способы действий в различных ситуациях, что отвечает задаче социализации обучающихся и их подготовке к активной жизнедеятельности. При этом развиваются не только способности к рассуждениям, но и умение обсуждать различные точки зрения в процессе взаимодействия с другими людьми, в том числе находить точки соприкосновения.
ТРКМ включает три стадии обучения «вызов – осмысление содержания – рефлексия». Эти стадии в совокупности определяют процесс движения учителя и обучающихся от поставленных целей к результатам обучения по освоению обучающимися определенного содержания (рис. 2).
Рассмотрим вышеописанный процесс на примере заданий для формирования математической грамотности «Клумба» и «Покупка смартфона».
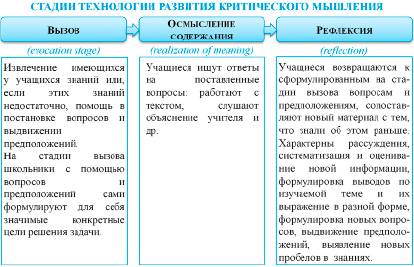
Рис. 2. Стадии технологии развития критического мышления
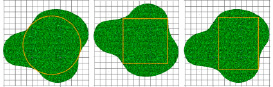
Рис. 3. Иллюстрация к заданию «Клумба»
Клумба
По данным опроса, большинство россиян хотели бы жить в загородном доме, к числу преимуществ которого они относят удобную планировку и большую площадь, хорошую экологию, возможность выращивать овощи и фрукты, комфортные условия для содержания животных и другие. Семья Сидоровых недавно приобрела участок земли, на котором собираются построить загородный дом и выращивать овощи и фрукты. Они также хотят разбить небольшую клумбу с цветами.
Стадия вызов
Обучающимся предлагается обсудить преимущества жизни в загородном доме, которые приведены в контексте задания, и определить возможные минусы. Также в процессе обсуждения следует вспомнить с обучающимися, в каких единицах измеряется площадь жилья и площадь участка земли под загородный дом.
Стадия осмысления содержания
Вопрос
Сидоровы отвели под клумбу небольшую часть участка. Мнения членов семьи разделились по поводу формы будущей клумбы: круглой, квадратной или прямоугольной. Какой формы должна быть клумба, чтобы ее площадь была максимальной (рис. 3), если длина стороны одной клетки равна 2 дм? Ответ запишите в м2.
На данном этапе важно обратить внимание обучающихся на возможности использования знаний геометрии для решения практических задач. С учетом математической подготовки обучающиеся могут самостоятельно или с помощью учителя нарисовать макет клумбы. И затем переходить к вычислению ее площади, соблюдая точность в подсчете клеток. Сначала можно вычислить площадь одной клетки – она равна 4 дм2. После чего нужно вычислить площадь клумбы в каждом из вариантов.
Sкруг = π ∙ 52 ∙ 4 ≈ 3,14 ∙ 52 ∙ 4 = 314 дм2 = 3,14 м2
Sквад = 82 ∙ 4 = 256 дм2 = 2,56 м2
Sпрямоуг = 7 ∙ 9 ∙ 4 = 252 дм2 = 2,52 м2
Стадия рефлексии
Данная стадия должна быть посвящена анализу полученных результатов и, возможно, постановке обобщенной задачи, связанной со сравнением площадей фигур с равными элементами. Также можно рассмотреть практические вопросы, которые могут быть связаны с задачей. Например, в каком из случаев для изготовления декоративного ограждения клумбы потребуется меньше материалов.
Покупка смартфона
Мобильный телефон за последние десятилетия стал неотъемлемой частью жизни современного человека. Кроме средства связи, он также выполняет множество функций: позволяет оперативно находить, передавать и хранить нужную информацию, напоминать о памятных датах, а различные дополнительные функции делают его незаменимым помощником не только в бытовой, но и деловой жизни.
Максим давно хотел обновить свой смартфон и купить более современную модель. Он изучил предложения интернет-магазинов, которые предлагают скидки, и подобрал несколько подходящих ему по техническим характеристикам вариантов (таблица).
Стадия вызов
На этой стадии обучающиеся должны осознать, что ценность покупки смартфона может быть рассмотрена с различных позиций: удовлетворения необходимым техническим характеристикам, цены, года выпуска. И оптимальность выбора следует рассматривать как комплексную характеристику. Следует предложить обучающимся расширить информацию о смартфонах дополнительными данными, которые также могут быть учтены при покупке (например, наличие и скорость доставки, стоимость доставки и др.).
Предложения интернет-магазинов
|
Модель |
Год выпуска |
Цена, руб. |
Скидка, % |
|
А |
2023 |
43000 |
8 |
|
Б |
2023 |
49000 |
20 |
|
В |
2024 |
62000 |
нет |
На стадии вызова следует предлагать несложные вопросы, которые помогут уточнить и дополнить информацию, например цену смартфонов со скидкой. В русле формирования математической грамотности он соответствует действию «формулировать», которое предусматривает распознавание в контексте задания математической информации. В данном задании – это выражение скидки в виде процентов.
Вопрос 1. Определите с учетом скидки самый дешевый и самый дорогой смартфон.
Ответ: самый дешевый с учетом скидки – модель Б; самый дорогой – модель В.
Стадия осмысления содержания
На данном этапе можно сразу переходить к основному вопросу, который непосредственно связан с выбором варианта покупки (вопрос 3), или же задать дополнительный вопрос (вопрос 2), который поможет дать ответ на основной вопрос.
Вопрос 2. Известно, что без замены аккумулятора средний срок службы моделей А и Б 2023 года составляет 3 года. Срок службы модели В 2024 года на 2 года больше моделей А и Б 2023 года. Замена аккумулятора в моделях А и Б продлевает срок службы на 2 года, а замена аккумулятора в этих моделях стоит 15 000 рублей. Какую из моделей выгоднее приобрести?
Ответ: выгоднее приобрести модель Б 2023 года со скидкой в 20% и заменой аккумулятора.
Вопрос 3. Максим хочет купить смартфон модели В 2024 года. Он накопил на него 40 000 р., а на недостающую сумму он хочет оформить кредит на один год под x% годовых. При каком наибольшем целом x стоимость года эксплуатации модели В 2024 года будет выгоднее использования более дешевой модели 2023 г. без замены аккумулятора?
Необходимо обратить внимание обучающихся, что выгодность покупки определяется не только финансовой составляющей, а включает также продолжительность его эксплуатации без покупки аккумулятора.
Для ответа на 3 вопрос необходимо составить математическую модель, которая имеет вид неравенства:
(62000 + (62000 – 40000) ∙ х / 100) : 5 < (49000 ∙ 0,8) : 3 .
Решая неравенство, получим, что его наибольшее целое решение – это x = 15.
Ответ: 15%.
Стадиярефлексии
Предусматривает обсуждение полученного ответа в рамках реальной ситуации. Важно, чтобы обучающиеся могли раскрыть как можно больше аргументов «за» или против выбранного варианта, привели примеры, их иллюстрирующие. Учителю важно обратить внимание, что выбор решения в реальной ситуации связан с множеством обстоятельств, не всегда решающее значение имеет финансовая сторона [12].
Заключение
Всесторонний анализ реальных ситуаций с позиции критического мышления, которые предлагаются в качестве контекста заданий по формированию математической грамотности, способствует обогащению социального опыта обучающихся, позволяет раскрыть межпредметный характер знаний, способствует пониманию и нахождению оптимальности выбранного решения с различных позиций.
Применение технологии развития критического мышления в процессе формирования математической грамотности, с одной стороны, обеспечивает погружение и лучшее осмысление обучающимися реальной ситуации, с другой – способствует повышению корректности выбора и применения математического инструментария, пониманию значимости математики для решения конкретных проблем.



